Результат измерения и его характеристики

♦ Измерение — это совокупность операций по применению техни­ческого средства, хранящего единицу физической величины, обес­печивающих нахождение соотношения (в явном или неявном виде) измеряемой величины с ее единицей и получение значения данной величины. ♦

Результат измерения представляет собой конечный продукт некоего производственного процесса, имеющего, как и любая другая продукция, свои показатели качества. Среди них важней­шим с учетом того, что речь идет об измерительном процессе, показателем качества является точность полученного результата.

Под точностью результата измерений понимают одну из его характеристик, отражающую близость к нулю погрешности.

Погрешность результата измерения — это отклонение резуль­тата измерения от истинного значения измеряемой величины. Так как истинное значение может быть получено только в ре­зультате бесконечного процесса измерений и требует непрерыв­ного совершенствования методов и средств измерений, то оно всегда остается неизвестным. В практических целях вместо ис-тинного значения используется действительное значение изме­ряемой величины, т.е. значение, полученное экспериментальным путем и настолько близкое к истинному, что в рамках постав­ленной измерительной задачи может быть использовано вместо него. Таким образом, погрешность измерения может быть вы­ражена зависимостью:

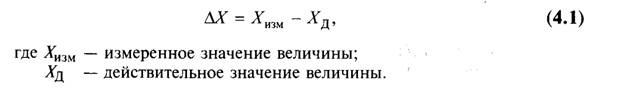
Значение АХ получило название абсолютной погрешности измерения. Абсолютная погрешность измерения выражена в единицах измеряемой величины. К сожалению, судить по зна­чению абсолютной погрешности о качестве измерения нельзя. Действительно, если известно, что погрешность измерения со­ставляет ± 1 мм, то оценить его качество затруднительно. Не­обходимо сопоставить значение абсолютной погрешности и значение измеренной величины. Эта задача решается введением понятия относительной погрешности измерения. Относительная погрешность измерения рассчитывается как отношение абсо­лютной погрешности к действительному (или измеренному) значению величины. Относительную погрешность выражают в долях единицы или в процентах в соответствии с зависимостью:

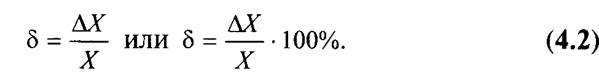
По закономернорти появления погрешности делятся на сис­тематические и случайные. При этом, как правило, самостоя­тельного значения они не имеют, а рассматриваются в качестве составляющих собственно погрешности измерения.

♦ Систематической погрешностью измерения называется состав­ляющая погрешности результата измерения, остающаяся постоянной или закономерно изменяющаяся при повторных измерениях одной и той же физической величины. ♦

Рекомендациями МИ 1317—04 «ГСИ. Результаты и характе­ристики погрешности измерений. Формы представления. Спо­собы использования при испытаниях образцов и контроле их параметров» установлено, что в качестве характеристик система­тической погрешности измерения целесообразно использовать среднее квадратическое отклонение неисключенной системати­ческой составляющей или границы, в которых неисключенная систематическая составляющая находится с заданной вероятно­стью (в том числе и с вероятностью, равной единице). Первая характеристика получила название точечной; вторая — интер­вальной. При проведении измерений принято вводить поправки в результаты и исключать систематическую составляющую. Од­нако всегда остаются погрешности вычисления и погрешности в определении значения самих поправок, а также систематические составляющие, ввести поправки на величину которых не пред­ставляется возможным ввиду их малости. Поэтому считается, что результат всегда содержит систематическую составляющую погрешности измерения, которую называют неисключенной.

♦ Случайной погрешностью измерения называется составляющая погрешности, изменяющаяся случайным образом (по знаку и зна­чению) при повторных измерениях одной и той же физической ве­личины, проведенных с одинаковой тщательностью. ♦

В качестве характеристик случайной составляющей погреш­ности используются ее среднее квадратическое отклонение и (при необходимости) нормализованная автокорреляционная функция.

Для характеристики погрешности измерений кроме характе­ристик случайной и систематической составляющих используют­ся среднее квадратическое отклонение и границы, в пределах ко­торых погрешность измерений находится с заданной вероятно­стью. Точечные характеристики рекомендуется использовать в случаях, когда результаты измерений (испытаний) используются совместно с другими результатами измерений, а также при расче­тах погрешностей величин, функционально связанных с результа­тами измерений (например, результатов косвенных измерений). Интервальные характеристики используются для решения опре­деленных технических задач. Если интервал ограничен наиболь­шим и наименьшим значениями погрешности измерений, а ис­тинное значение погрешности находится внутри него с заданной вероятностью, то этот интервал называется доверительным интер­валом, а вероятность — доверительной вероятностью.

В связи с тем, что истинное значение и измеряемой величи­ны, и погрешности результата измерения неизвестны, а измере­ниям подвергаются все больше величин, для которых само оп­ределение «физическая величина» неприменимо, в последнее

время для оценки качества измерительной информации все ча­ще используется понятие «неопределенность измерений».

• Неопределенность измерений — параметр, связанный с резуль­татом измерений и характеризующий рассеяние значений, которые можно приписать измеряемой величине. ♦

Этим параметром может быть среднее квадратическое откло­нение (стандартное отклонение), число, кратное ему, или поло­вина доверительного интервала. Неопределенность состоит, как правило, из многих составляющих. Некоторые из этих состав­ляющих могут быть оценены экспериментально определенными средними квадратическими отклонениями в статистически рас­пределенной серии результатов измерений. Другие составляю­щие, которые также могут быть оценены стандартными откло­нениями, базируются на данных эксперимента или другой ин­формации. Структурно неопределенность результата измерения обычно состоит из нескольких составляющих, которые могут быть вызваны следующими причинами:

• неполным описанием (неточным определением) измеряе­мой величины;

• несовершенной реализацией описания (несовершенством выбранного метода измерения);

• неполным учетом влияющих величин и несовершенством методов их измерения;

• субъективными погрешностями оператора;

• конечной величиной разрешающей способности приме­ненных средств измерений;

• неточными значениями констант и других параметров, по­лученных от внешних источников и используемых в алго­ритме обработки результатов эксперимента, и др.

Эти составляющие определяют также и погрешность измере­ния. Еще раз отметим, что основное различие между неопреде­ленностью и погрешностью состоит в представлении о сущест­вовании истинного значения. Если в начальный постулат зало­жено существование истинного значения, то это неизбежно приводит к определению погрешности измерения. Если сущест­вование истинного значения отрицается, то следствием является представление о неопределенности результата измерения.

Составляющие неопределенности по способу получения их численных значений подразделяются на две категории: А и В.

К категории А относят составляющие, численные значения ко­торых получены на основе статистического анализа эксперимен­тальных данных. Это стандартные отклонения (средние квадратические отклонения). При достаточно большом числе наблю­дений данные оценки (среднее арифметическое значение и стандартное отклонение) являются наилучшими. Составляющие, относимые к категории В, оцениваются любым другим спосо­бом, кроме статистического анализа. Для их оценки использует­ся аппарат субъективной теории вероятностей на основе апри­орной информации — справочных материалов, экспертных оце­нок, данных предварительных измерений и т.д.