И характеристики распределения случайных величин

Для оценки составляющих погрешности и неопределенности результата измерения используются такие характеристики, как среднее арифметическое значение, среднее квадратическое от­клонение и др. Для лучшего понимания предлагаемого материала рассмотрим некоторые понятия и определения теории вероятно­стей и математической статистики, применяемых в метрологии.

Наличие случайной составляющей погрешности измерения приводит к тому, что для получения результата измерения целе­сообразно рассматривать измеряемые величины как случайные. Кроме того, сами случайные погрешности могут быть определе­ны только с привлечением аппарата теории вероятностей, кото­рая представляет собой науку, изучающую закономерности слу­чайных явлений. Теория вероятностей устанавливает законо­мерности только для массовых явлений, т.е. таких явлений, ко­торые могут повторяться многократно при одних и тех же усло­виях. В метрологии массовыми являются измерения, проводи­мые с помощью одного и того же средства измерений, характе­ристики множества средств измерений одного типа и др.

Для того чтобы охарактеризовать случайную погрешность измерения, обратимся к определению случайного события и его вероятности.

Случайным называется событие, которое в данном опыте может произойти или не произойти. Каждый опыт может быть охарактеризован множеством событий. Например, при игре в кости один и тот же опыт может быть представлен следующими событиями: «выпало 1»; «выпало 2»; «выпало 3»; «выпало 4»; «выпало 5»; «выпало 6». Точное определение ожидаемого исхода опыта — установление случайного события — имеет важнейшее значение. Обозначим случайное событие А и будем иметь в ви­ду, что большинство событий в метрологии понимаются как выполнение соотношения

Каждое из событий в опыте обладает какой-то степенью возможности: одни — большей, другие — меньшей. Для количе­ственного сравнения случайных событий по степени их возмож­ности используется количественная характеристика каждого случайного события, которая выражается числом тем большим, чем более возможно данное событие. Эту характеристику назы­вают вероятностью случайного события и обозначают, как пра­вило, Р. Таким образом, вероятность случайного события явля­ется численной мерой объективной возможности этого события и определяется по формуле:

Назначение события оказывает прямое влияние на значение вероятности. Так, если речь идет об игре в кости и первый из играющих имеет результат 4, то ожидаемых событий для второго играющего — два: выигрыш или поражение. Для выигрыша не­обходимо получить 5 и 6. Таким образом, в этом случае вероят­ность выигрыша для него составит Р(5,6) = 2/6 = 1/3. Вероят­ность будет совсем другой, если в качестве события А рассмат­ривать вероятность проигрыша или если первый из играющих набрал, например, два очка.

Определение числа п — числа всех возможных исходов опы­та — часто весьма затруднительно, но самое главное, что в мет­рологии попросту невозможно ввиду ограниченной возможно­сти повторения опытов. Число т — количество раз, когда собы­тие А в результате опыта наступило, в метрологии также опреде­ляется на основе ограниченного числа опытов. Поэтому в прак­тике метрологических работ вместо вероятности используют частоту появления случайного события А:

Частоту Р*(А) ввиду ее использования в роли вероятности в практике метрологических работ называют статистической ве­роятностью.

Свойства случайной величины исчерпывающе описываются законом распределения случайной величины, который представ­ляет собой соотношение, устанавливающее связь между воз­можными значениями случайной величины и соответствующи­ми им вероятностями.

Случайные величины можно разделить на дискретные и не­прерывные. Значения дискретной случайной величины могут быть перечислены. Значения непрерывной случайной величины непрерывно заполняют некоторый интервал. Случайные по­грешности измерений относятся к непрерывным случайным ве­личинам, но проявляются часто в виде некоторого набора зна­чений, т.е. дискретно. Поэтому к ним применимы понятия и непрерывных, и дискретных случайных величин.

Для дискретной случайной величины удобной формой опи­сания закона распределения является ряд распределения — таб­лица, в которой перечислены возможные значения случайной величины х, и соответствующие им значения вероятности />,-(табл. 4.1).

Еще одной, более удобной, универсальной и часто приме­няемой на практике формой описания закона распределения случайной величины является функция распределения F(x), кото­рая определяет вероятность того, что случайная величина X бу­дет принимать значения, меньшие некоторого ограничения х:

Рис. 4.2. График функции распределения дискретной случайной величины

Так как функция распределения непрерывной случайной величины (см. рис. 4.1) является непрерывно дифференцируе­мой, то для ее описания часто пользуются первой производной

или плотностью распределения. Плотность распределения представляет собой одну из форм описания закона рас­пределения, применяемых для непрерывных случайных величин. Плотность распределения обозначается, как правило, F'(x) или f(x). График плотности распределения представлен на рис. 4.3.

Рис. 4.3. График плотности распределения непрерывной случайной величины

Взаимосвязь между функцией распределения и плотностью распределения случайной непрерывной величины имеет вид:

Законы распределения позволяют решать любые практиче­ские задачи, связанные со случайными величинами, и в этом их безусловное достоинство. Однако использование законов рас­пределения для решения практических метрологических задач связано также и с определенными проблемами. Прежде всего, чтобы определить закон распределения, необходимо провести достаточно трудоемкое исследование (требуются специальные оборудование и методика, многократные измерения, качествен­ный анализ и т.д.), что не всегда возможно. Наибольшее удобст­во для практического использования предоставляют числовые характеристики случайной величины — математическое ожида­ние и дисперсия случайной величины, которые характеризуют значение случайной величины и ее разброс соответственно. Чи­словые характеристики связаны с законами распределения, по­этому иногда используют и другие показатели, но математиче­ское ожидание и дисперсия — наиболее употребляемые, основ­ные числовые характеристики случайной величины.

Математическим ожиданием случайной величины называет­ся число, определяемое для непрерывных случайных величин по зависимости:

Из формулы (4.12) следует, что значение случайной величи­ны х может быть определено величиной среднего арифметиче­ского значения X, полученного по результатам многократных наблюдений этой величины. Среднее арифметическое значение может сильно отличаться от действительного значения измеряе­мой величины за счет:

• наличия систематических составляющих погрешности из­мерения, поэтому для его получения категорически необ­ходимо введение поправки на величину систематической составляющей погрешности;

• возможности появления грубой погрешности измерения, для устранения которой проводят минимум три измерения;

• несоответствия среднего арифметического значения закону распределения случайной величины, в связи с чем обра­ботка результатов измерений всегда должна начинаться с определения (указания) принятого закона распределения.

Итак, после определения среднего арифметического значе­ния случайной величины на числовой оси можно отложить ее значение — среднее арифметическое. Легко представить слу­чай, когда для двух рядов измерений средние арифметические значения равны. Значит, одного этого значения недостаточно, чтобы охарактеризовать случайную величину. Необходима ха­рактеристика разброса. В качестве ее можно принять разность значений x_max — x_mшn, полученных при измерениях результатов. Эта характеристика получила название размаха значений, слу­чайной величины.

Однако при равенстве и средних арифметических значений, и размахов два ряда измерений будут отличаться степенью груп­пирования (концентрации) полученных результатов, например, относительно среднего арифметического значения. Подходящей характеристикой, позволяющей индивидуализировать разброс результатов многократных измерений, является суммирование величины их отклонений от среднего арифметического значе­ния. Эта характеристика получила название дисперсии случай­ной величины D(x). По определению дисперсия случайной ве­личины — это математическое ожидание квадрата соответст­вующего отклонения случайной величины х от ее математиче­ского ожидания т(х):

В формулах (4.13)—(4.15) рассматривается квадрат отклоне­ний значений случайной величины от ее математического ожи­дания, что позволяет устранить взаимную компенсацию поло­жительных и отрицательных значений отклонений при их сум­мировании. Дисперсия случайной величины имеет размерность квадрата размерности собственно величины, что затрудняет ис­пользование дисперсии в практике метрологических работ. По­этому в метрологии чаще используется понятие «среднее квадра-тическое отклонение» S(x), которое принимается равным поло­жительному корню квадратному из значения дисперсии:

Корректировка знаменателя в зависимости (4.17) позволяет компенсировать приведенные выше допущения за счет увеличе­ния значения S(x). При очень большом числе измерений (п > 15) корректировка знаменателя не сказывается на величине S(x); при малом — имеет большое значение, причем тем больше, чем меньше п.

Форма кривой плотности распределения (см. рис. 4.3) от­ражает вид функции f(х). Во многих характерных случаях эти функции исследованы и результатами этих исследований пользуются на практике. Среди наиболее часто употребляе­мых распределений прежде всего необходимо выделить так называемое нормальное распределение, или распределение Гаус­са. Это обусловлено тем, что если случайная величина пред­ставляет собой сумму трех и более составляющих, то ее рас­пределение, независимо от формы распределения слагаемых, описывается уравнением:

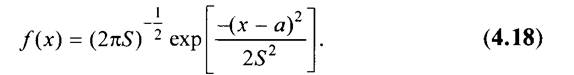
График функции нормального распределения представлен на рис. 4.4.

В связи с тем, что большинство процессов измерения харак­теризуются большим числом составляющих погрешности изме­рения и это предоставляет право без проведения каких бы то ни было исследований принять для случайной погрешности нор­мальное распределение, нормальный закон стандартизован и является одной из двух установленных в нормативной докумен­тации форм законов распределения, применяемых при обработ­ке результатов многократных измерений.

Если результаты наблюдений имеют нормальное распределе­ние, то средние арифметические значения (результаты измере­ния) также распределены по нормальному закону. Это дает воз­можность оценить разброс результатов измерений, проводимых сериями (например, при проведении операций допускового контроля), по формуле:

В соответствии с зависимостями (4.6) и (4.18) функция рас­пределения F(x), распределенной по нормальному закону, имеет вид:

Второй установленной в нормативной документации формой закона распределения является равномерное распределение. Рав­номерное распределение используется для описания таких вели­чин, как вариация показаний средств измерений, неисключенная систематическая погрешность, погрешность округления. Равномерное распределение описывается уравнениями:

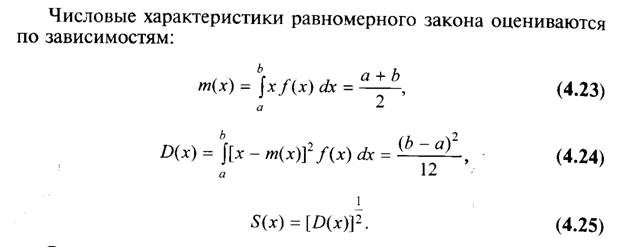
Равномерное распределение обладает наибольшей неопреде­ленностью для всех случайных величин в выбранном интервале и может рассматриваться как худший случай.

Для количественной оценки погрешности измерения часто пользуются так называемыми доверительными интервалами и соответствующими им доверительными вероятностями. Довери­тельные интервалы позволяют оценить диапазон значений вели­чины, в котором с принятой вероятностью находится неизвест­ное истинное значение измеряемой величины. Пусть при изме­рении физической величины с истинным значением Х _Иполучен результат измерения X. Задаваясь значением вероятности Р_Д то­го, что случайная погрешность измерения находится внутри не­которого интервала ∆_гр = ± ε, необходимо найти граничные значения этого интервала, удовлетворяющие условию:

Виды измерений.

⇐ Предыдущая891011121314151617Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: