 |
Обработка результатов прямых многократных измерений
|
|
|
|
Методика получения результатов при проведении многократных прямых измерений установлена ГОСТ 8.207—76 «ГСИ. Прямые измерения с многократными наблюдениями. Методы обработки результатов наблюдения. Основные положения». Перед рассмотрением методики напомним, что ГОСТ 8.207 разработан и утвержден в период действия ныне отмененных ГОСТ 16263 на термины и определения в области метрологии, ГОСТ ов серии «П.», устанавливающих правила математической статистики при определении закона распределения, и отсутствия каких бы то ни было представлений о неопределенности результатов измерений.
Основные операции и их последовательность Методика обработки результатов прямых многократных измерений включает в себя следующие операции:
• определение наличия грубых погрешностей и исключение промахов;
• исключение известных систематических погрешностей из результатов наблюдений;
• вычисление среднего арифметического исправленных результатов наблюдений, принимаемого за результат измерения;
• вычисление оценки среднего квадратического отклонения результата наблюдений;
• вычисление оценки среднего квадратического отклонения результата измерения;
• проверку гипотезы о том, что результаты наблюдений принадлежат нормальному распределению. Проверку гипотезы о том, что результаты наблюдений принадлежат
нормальному распределению, следует проводить с уровнем значимости q от 10 до 2%. Конкретные значения уровней значимости должны быть указаны в конкретной методике выполнения измерений;
• вычисление доверительных границ случайной погрешности (случайной составляющей погрешности) результата измерения;
• вычисление границ неисключенной систематической погрешности (неисключенных остатков систематической погрешности) результата измерения;
|
|
|
• вычисление доверительных границ погрешности результата измерения. Для определения доверительных границ погрешности результата измерения доверительную вероятность Р, как правило, принимают равной 0,95. В тех случаях, когда измерение нельзя повторить, помимо границ, соответствующих доверительной вероятности Р = 0,95, допускается указывать границы для доверительной вероятности Р = 0,99. В особых случаях, например при измерениях, результаты которых имеют значение для здоровья людей, допускается вместо Р = 0,99 принимать более высокую доверительную вероятность.
Подготовка результатов наблюдений к обработке Способы обнаружения грубых погрешностей должны быть указаны в методике выполнения измерений. Важное значение при определении наличия грубых погрешностей имеет вопрос о законе распределения результатов измерений. Как правило, результаты измерений считают принадлежащими к нормальному распределению. Для нормального распределения разработано несколько критериев оценки наличия грубых погрешностей. В целом их действие основано на представлении о том, что измеряемая величина может характеризоваться большим количеством измерительной информации (генеральной выборкой) и ее ограниченным количеством (выборкой). Результаты обработки будут тем точнее, чем на больший объем информации они опираются. Поэтому критерии отнесения погрешностей к грубым можно разделить на критерии сопоставления имеющихся результатов с характеристиками генеральной выборки и характеристиками распределения собственно полученных результатов.
Если известны характеристики генеральной выборки (среднее квадратическое отклонение) или они могут быть получены в результате обработки предшествующих опытов, то следует пользоваться критериями, основанными на известном генеральном среднем квадратическом отклонении, и только когда оно неизвестно и нет возможности его получить, следует пользоваться критериями, основанными на использовании выборочного среднего квадратического отклонения. Так как грубые погрешности способны заметно повлиять на результат измерения, рассмотрим некоторые, наиболее употребляемые из известных критериев.
|
|
|
1. Значение генерального среднего квадратического отклонения неизвестно.
В таком случае имеются результаты наблюдений, составляющие упорядоченную выборку, которую можно представить в виде:

Сомнению могут быть подвергнуты, естественно, результаты, заметно отличающиеся по величине от остальных, т.е. либо наименьший (x 1), либо наибольший (хn).
Среднее арифметическое значение выборки [хи хп] составит:
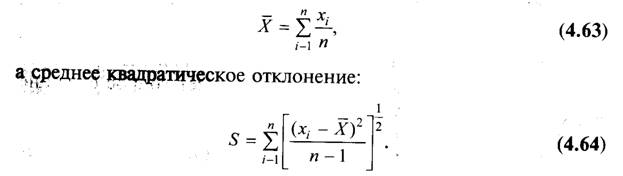
Принадлежность х1 или хп к данной выборке, распределенной по нормальному закону, определяется по значению соотношений:
ношений:

Если значения Un или U1 превысят критические значения р, приведенные в табл. 4.3, то соответствующий результат не принадлежит нормальному распределению и из результатов измерений должен быть исключен.
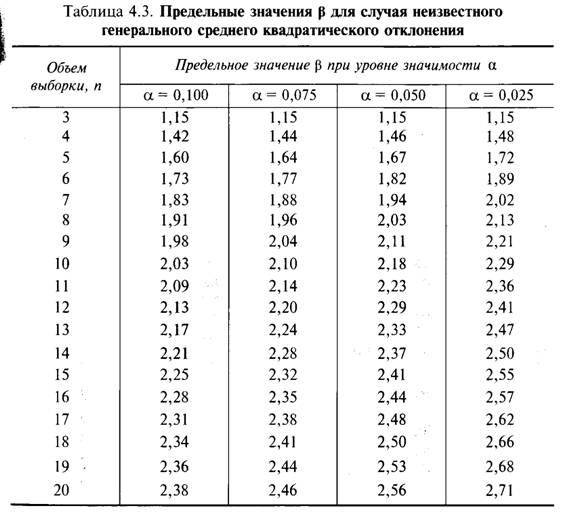
2. Значение генерального среднего квадратического отклонения известно. Значение генерального среднего арифметического неизвестно.
Практика измерений столь обширна, что довольно часто встречается ситуация, когда из предшествующих опытов значение генерального среднего квадратического (обозначим его а Для различия со средним квадратическим выборки S) известно, а генеральное среднее арифметическое — нет. В этом случае составляют упорядоченную выборку (4.62) и подсчитывают среднее арифметическое (4.63). По полученным данным подсчитывают значения коэффициентов:
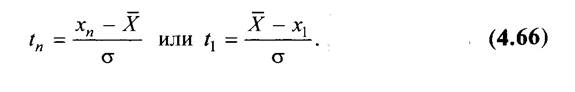
Если полученные значения превысят критические значения β, приведенные в табл. 4.4, то соответствующие результаты анормальны и из полученного ряда измерений должны быть исключены.
Таблица 4.4. Предельные значения р для случая известного значения
|
|
|


