 |
Закон сохранения энергии в механике
|
|
|
|
Рассмотрим с-му n мат. точек. Пусть mi, vi соответственно масса и скорость. Пусть на i-ю точку со стороны k-ой действует внутренняя консервативная сила fik. Пусть Fi - равнодействующая внешних консервативных сил, и Fi* - это равнод-я внешних неконсервативных сил на i-ю точку.
По 2-му закону Ньютона имеем ур-е дв-я с-мы:

Умножим обе части ур-я (1) на выр-е vidt=dri, и просуммируем по всем точкам с-мы:
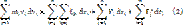

Выр-е слева в ф-ле (2) – это и есть изменение Ek. 1-е слагаемое справа в (2) есть работа внутр. консервативных сил и она равна убыли Ep взаимодействия:

2-е слагаемое в (2) есть работа внеш. консерват. сил и она равна убыли Ep c-мы во внешнем поле с-мы. Последнее слагаемое в (2) есть работа на с-мой внеш. неконсерв. сил. С учетом вышесказанного:
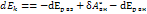
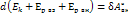
Пусть внешних сил нет:
d( )=0
)=0
 – закон сохранения энергии (зсэ)
– закон сохранения энергии (зсэ)
Полная мех. энергия замкнутой консерват. с-мы тел, на кот. действуют лишь консерв. силы, остается постоянной. ЗСЭ – общефизический закон.
ЗСЭ связан с однородностью времени, т.е. симметрии по отношению к сдвигу времени. Однородность времени не означает независимость закона физ. явлений от выбора начала отсчета времени. Такая инвариантность относительно сдвига времени означает ненаблюдаемость абсол. времени.
11о. Закон сохранения момента импульса.
Пусть твёрдое тело вращается вокруг неподвижной оси Z, тогда элементарная работа всех внешних сил равна приращению ЕК вращающегося тела (по з-ну сохранения Е), т.е.:
dA = dEK
dA = MZ*dφ
EK = Iz*ω2/2; Iz = const
MZ*dφ = Iz*ωdω||: dt
MZ*(dφ/ dt) = Iz*ω(dω/dt)
MZ = Iz*(dω/dt)
MZ = d(Iz*ω)/dt
MZ = dLZ/dt
Пусть внешних сил нет, тогда MZ = 0, поскольку моменты внутренних сил (3-ий з-н Ньютона) взаимно скомпенсированы:
MZ = 0; dLZ/dt = 0; LZ = const (з-н сохранения момента импульса).
|
|
|
Суммарный момент импульсов замкнутой системы тел (частиц) сохраняется.
I1*ω1 = I2*ω2
З-н сохранения импульса связан с изотропностью пространства, т.е. симметричностью пространства, означает равноправие всех пространственных направлений.
Поворот в изотропной системе пространства как целого не меняет свойств системы и з-нов её движения.
12о. Движение тела переменной массы.
Получим уравнение движения ракеты (уравнение Мещерского):
Масса ракеты m меняется со временем. Пусть момент времени t, скорость  и масса m. По истечении времени dt, масса ракеты уменьшится и станет (m - dm), где dm – масса сгоревшего топлива, скорость возрастёт и станет
и масса m. По истечении времени dt, масса ракеты уменьшится и станет (m - dm), где dm – масса сгоревшего топлива, скорость возрастёт и станет 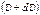 ,
,  отн – скорость истекающе-сгорающего топлива относительно ракеты.
отн – скорость истекающе-сгорающего топлива относительно ракеты.
Изменение импульса системы равно конечному импульсу минус начальный импульс m  .
.
 ракета топливо
ракета топливо

 ||: dt
||: dt
 - уравнение Мещерского
- уравнение Мещерского
 - сила действия на ракету
- сила действия на ракету
 - уравнение Мещерского
- уравнение Мещерского

Спроектируем уравнение Мещерского на направление движения ракеты, тогда получим:
 = 0
= 0
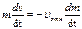
 ||:
||: 
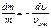
Проинтегрируем:
 ,
, 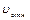 = const
= const
Или спотенцируем:

Пусть в момент времени t = 0, скорость ракеты равна 0, а масса m 0 :
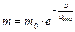 - формула Циолковского
- формула Циолковского
Для химического топлива скорость сгорания: 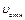 = 4 км/с
= 4 км/с
Первая космическая скорость: 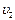 = 8 км/с
= 8 км/с
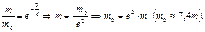
13о. Кинематика гарманических колебаний
Колебание – движение или процессы отличающиеся повторяемостью во времени. Колебания физич-ой велечины х называются гарманическими, если она изменяется со временем по з-ну cos или sin, т.е.:
х = Аcos(ωt + φo)
A > 0 – амплитуда – максимальное значение колеблющейся величины х.
ω – круговая, угловая, циклическая частота.
t – текущее время (начало отсчёта времени определяет φo – начальная фаза).
(ωt + φo) – фаза гарманических колебаний.
При заданной амплитуде А фаза однозначно определяет велечину х.
Начальная фаза и фаза измеряются в рад.
|
|
|
 - А≤ х ≤ А
- А≤ х ≤ А
Т – период колебаний – промежуток времени, по истечении которого колебания повторяются, а фаза получает приращение 2π.
ω(t + Т) + φo = ωt + φo + 2π
ωТ = 2π

Величина обратная периоду:
ν = 1/Т – частота колебаний – число колебаний за единицу времени.
[ν] = Гц (герц)
ГК графически изображаются методом вращения вектора амплитуды или иначе методом векторных диаграмм.
Пусть тМ вращается по окружности радиуса А с постоянной угловой скоростью ω:
 Коор-ты тМ меняются по гармоническому з-ну: х = Аcos(ωt + φo).
Коор-ты тМ меняются по гармоническому з-ну: х = Аcos(ωt + φo).
14о. Гармонический осциллятор.
Получим дифференциальное уравнение описывающее систему совершающую ГК. Для этого вычислим 1-ую и 2-ую производные по времени от ГК величины х:
(1) х = Аcos(ωt + φo)
(2) 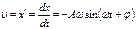
(3) 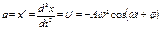

(*) 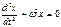 - уравнение гармонического осциллятора.
- уравнение гармонического осциллятора.
Система, поведение которой описывает выражение (*) наз-ся гармоническим осциллятором.
Решением уравнения (*) является выражение:
х = Аcos(ωt + φo)
Покажем, что на тело совершающее ГК действует квазиупругая сила описываемая з-ном Гука:
F = - kx
F = ma
a из (3): F = - m 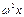 = - kx, где k = m
= - kx, где k = m 
Найдём полную механическую энергию гармонического осциллятора:


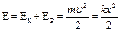 - з-н сохранения энергии для гармонического осциллятора.
- з-н сохранения энергии для гармонического осциллятора.
Энергия ГК величины пропорциональна квадрату амплитуды: E ~ А2
Гармонический осциллятор является маятником.
15о. Примеры гармонических осцилляторов.
Маятники: пружинный, математический, физический.
Пружинный маятник – тело с массой m соединённое с пружиной и совершает колебания при выведении из положения равновесия при действии силы Гука.
 Fупр = - kx
Fупр = - kx
По II-му з-ну Ньютона имеем уравнение движения этого маятника:
ma = F
m 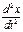 = - kx ||: m
= - kx ||: m
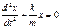 ;
; 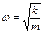

х = Аcos(ωt + φo)

Математический маятник – математическая точка (m), подвешенная на невесомой нерастяжимой нити длиною l и совершает колебания под действием силы тяжести при выведении точки из положения равновесия.
Основное уравнение динамики вращательного движения для математического маятника.
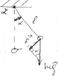



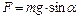
 ||: l
||: l
(1) 


(1) уравнение колебаний математического маятника, если α – мало, то  (рад)
(рад)
α ≤ 100 ≈ 0,17 рад
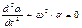 - уравнение колебаний математического маятника.
- уравнение колебаний математического маятника.
Малые колебания математического маятника гармонические.
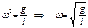
α = αо cos(ωt + φo)
|
|
|

Если колебания не малые, то разлагая sin в ряд, получаем:

Получим из (1) уравнение не линейных колебаний:

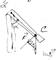 Физический маятник – твёрдое тело, совершающее колебания под действием силы тяжести вокруг оси, не проходящей через центр тяжести.
Физический маятник – твёрдое тело, совершающее колебания под действием силы тяжести вокруг оси, не проходящей через центр тяжести.
Получим уравнение, описывающее колебания физического маятника:
ZC = l (от точки подвеса до центра тяжести)
Уравнение движения:
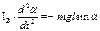
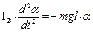 (α в рад)
(α в рад)

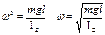
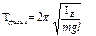
Малые колебания гармонические.
|
|
|


