 |
Вынужденные колебания. Резонанс.
|
|
|
|
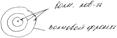Вынужденными наз. Колебания возникающие в колеблющейся системе под действием внешней периодической силы. Пусть внешняя вынужденная сила меняется по периодическому закону 
. Тогда с учетом силы трения, квазиупругой и вынужденной сил можно записать виде: 
;
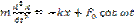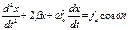(1); 
.
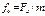Можно убедиться непосредственной проверкой, решение дифф. уравнения затухающих колебаний(ур-ие 1) имеет вид:
(2) 
+ 
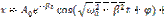
(2) Решение ур-ия (1) складывается из общего решения ур. (1) без правой части(
) и частного решения ур. (1) с правой частью. Из решения (2) вытекает, что для установившегося движения 
первое слагаемое в (2) обращается в 0 и роль играет только второе слагаемое. Резонанс- резкое возрастание амплитуды вынужденных колебаний при некоторой частоте 
. При отсутствии трения (сопротивления) рез. частота 
совпадает с собственной частотой ω. 
; 
;
из этой формулы вытекает, что при отсутствии трения, когда 
, резонансная амплитуда устремляется в 
, а резонансная частота совпадает с собственной частотой 
.
Рассмотрим резонанс вынужденных колебаний с учетом квазиупругой и вынужденной сил, но без учета трения: 
; будем искать решение последнего ур-ия виде: 
; 
; 
; 
(
) 
; 
; 
; 
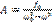
Если 
, то 
.
Упругие волны в средах.
Волна –процесс распространения колебаний в среде. Для распространения волны необходим источник волны. Волны в среде распространяется с некоторой скоростью 
. При распространении волны в среде частицы не переносятся с волной, а совершают колебания возле положения равновесия. Механические или упругие волны представляют собой процесс распространения возмущений в упругой среде. Различают волны продольные и поперечные. Волна продольная если колебания частиц среды происходит вдоль распространения волны. Волна поперечная если колебание частиц происходит в направлении перпендикулярном направлению распространения волны. Продольные волны могут распространяться во всех средах (газ, жидкость, твердые тела) при диффузии сжатия и растяжения. Поперечные – только в твердых телах, при диффузиях сдвига. Упругая волна наз. Синусоид-но гармонической если колебания частиц среды гармонические. 
(E-модуль Юнга, 
|
|
|
(G-модуль сдвига); 
. Фронт волны - геометрическое место точек до которых дошли колебания. Волновая поверхность- совокупность точек колеблющихся в одной фазе.
21о.Бегущие волны. Фазовая скорость. Длина волны. Волновое число.
Бегущими наз-тся волны(в.), кот-ые переносят энергию в пр-стве.
Ур-ние в. наз-тся выр-ние, задающее смещение колеб-хся частиц, как ф-цию корд-т xyz и времени t.
Найдём ур-ние поперечной одномерной плоской бегущей волны.
Волна плоская, если фронт плоский.
Пусть т.М колеблется в упругой среде вдоль оси 
около положения равн-сия по гарм-ому закону, т.е. 
Т.к. среда упр-ая, то кол-ния т.М будут перед-ся соседним т. среды и вдоль оси х будет распр-ся поперечная среда. В т.Мх с координатой х дойдут с запаздыванием по времени
Если кол-ния т.М незатух-щие, то т.Мх будет кол-тся с такой же частотой 
и амплитудой А, но с запаздыванием по времени на 
Если учесть нач-ую фазу
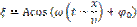
В ур-ии волны -смещение частиц среды от пол-ния равновесия.
А – амплитуда (по опред-ию +) наибольшее смещение частиц среды от положения равн-сия.
– циклическая частота.
Х – расстояние от источника волны до точки, в кот-ой рассматр-тся смещ-ие 
t – текущее время, начало отсчёта которого опред-тся начальной фазой 
Гребнями волны наз-ся максимальные точки смещения.
Впадины – это 
– А.
Фаза в. – выр-ние, стоящее под cos.
Ур-ние (*) есть ур-ние в., распред-щейся вдоль полож-го напр-ния оси х.
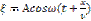- в отриц-ом напр-ии
|
|
|
Длина в. – расст-ие между частицами среды, для кот-ых разность фаз =2 
,т.е. с учётом сказанного имеем
или 
-число кол-ний
Период кол-ий – время, за кот-ое частица среды сов-ет полное кол-ие
; 
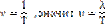Длина в. – расст-ие, на кот-ое распр-тся опр-ая фаза кол-ия, за время = периоду.
За период Т в. распр-тся на свою длину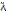 
.
Запишем др. выраж-ия для ур-ия в.
Волн-ое число – число, уклад-щееся в 2 
.
Ур-ие в. можно записать в других видах:
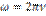
В комплексном виде
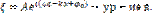
Ур-ие сфер-ой в.
Пусть при волн-ом процессе фаза постоянна, т.е.
Продифф-ем
; 
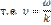
Фазовая скорость зависит от частоты.
Среда, в кот-ой наблюд-тся завис-сть фаз.ск.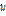 
в. от её частоты, наз-тся дисперсной.
Дисперсия- разложение белого цвета в спектр при прохождении света через стекл-ую призму.
|
|
|
