Связь массы, энергии, импульса в СТО

Соотношение справедливо для всех видов энергии. Эйнштейн показал, что масса и энергия частицы связ. соотношением:

– эн-гия покоя (измеренная в сопутствующей СО).

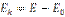(разность полной эн-гии движущегося тела и его эн-гии покоя)

Найдём соотнош. между полной эн-гией и импульсом частицы:

; , , ,

 

 

, где – инвариантно, - const

Если покоя фотона = 0, то импульс фотона:

 

 

34^о. Эффект Доплера

1842 - был открыт в акустике.

Эф.Допл. в оптике есть возрастание частоты света, воспринятой приемником по сравнению с частотой, излучаемой источником при взаимном сближении источника и приёмника и уменьш-ой частоте, при взаимном удал. источника и приёмника.

Пусть источник света покоится в системе S,а приёмник света движется по оси X со скор. ύ=const вместе с системой .

Ур-ние плоской световой волны, идущей от источника к приёмнику в сист.S имеет вид:

E(x,t)=E₀ (1)

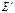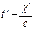(x,t)= cos ()(2)

Координ. и время t связаны с корд. и временем в сист. преобразованиями Лоренса, к-рые имеют вид (система (3)):

Соотн.(3) подст.в (1):

ώ

=

(4)

Сравнивая выраж.(2)и (4),получаем,что частота

В последней формуле берётся со знаком + при взаимном удалении источника и приёмника света и воспринимая частота уменьшается в сравнении с частотой источника.

берётся со знаком – при взаимном сближении ист. И приёмн.,и частота возрастает.

 

35^о. Принцип эквиваленности.Понятие о ОТО

СТО рассм. инерциальную сист. отсчёта, в ОТО рассм. и усоренно движущуюся систму. Принцип относительности обобщается на такие системы отсчёта: ОТО включает теорию тяготения.

Согласно Эйнштейна пространство Эвклидово (плоское) лишь при наличии масс, наличие масс приводит к появлению поля тяготения и к исправлению пространственных масс. Пространство становится неэвклидовым (кривым).

Движение тел по инерции в таком кривом пространстве уже происходит не по прямым линиям, как Эвклидово, а по некоторым кратчайшим кривым-геодезическим. Отклонение от прямолинейного движения обуславливается кривизной пространства, вызванной наличием масс, трактуется как поле тяготения этих масс, тогда движение в поле тяготения не есть движение под действием сил тяготения, а есть движение по инерции в пространстве с кривизной, вызванной наличием тяготеющих масс -принцип эквивалентности.

Инертная масса = гравитационной

Из ур-я Эйнштейна два следствия:

1)Расширение вселенной со временем.

2)Существование чёрных дыр.

Е_Р = Е_К → GMm/r_д = mс²/2

r_д = 2GM/ с²; Земля должна иметь радиус r_д = 0,5 см (чтобы стать чёрной дырой).

 

36^о. Равновесие и течение жидкости и газа

Гидроаэродинамика изучает равновесие и движение жидких и газообразных сред и их взаимодействие с твердыми телами. Для жидкости и газов характерна текучесть, т.е. малая сопротивляемость деформации сдвигов, поэтому они не проявляют упругость формы и легко принимают форм сосуда, в к-ром находится в поле тяжести. Жидкости, в отличие от газов, малосжимаемы, т.е. . Опыт показывает, что если в покоящуюся простую (неизотропную) жидк. поместить пластинку, то силы, действующие на пластинку одинаковые с обеих сторон и направлены по нормали к пластине(равны по модулю и противоположны по направлению).

Давление в жидкости:

Есть отношение нормальной силы, распространяющейся по площадке, к площади площадки.

Для простой жидкости справедлив закон Паскаля: «Давление в любом месте жидкости одинаково по всем направлениям, и внешнее давление одинаково передаётся по всему объему, занятому покоящейся жидкостью».

Давление в 1Па возникает при действии силы в 1Н, равномерно распределяющейся по поверхности и направлено по нормали к поверхности = .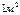

Па .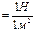

Давление, обусловленное весом несжимаемой жидкостью, расположенной в поле тяжести, называется гидростатичесим.

Рассм. столб жидкости высотой h и площадью поперечного сечения S,

Для тел, погруженных в жидкость или газ справедлив закон Архимеда: « На тело, погруженное в жидкость или газ, действует выталкивающая сила, направленная вверх и численно = весу жидкости, вытесненной телом».

приложена к центру давления, т.е. центру тяжести жидкости в форме погруженного тела.

Жидкость идеальная, если элементы движутся бес трения(отсутствуют силы вязкости и энергия движения не расходуется на трение и тепло справедлив закон сохранения энергии). Для описания течения жидкости используется 2 метода: Лагранжа и Эйлера.

В методе Лагранжа используется сопутствующая система отсчета, в Эйлера – фисированная система отсч. (не движ. с частицей), тогда такой частице жидкости соответствует свой вектор скорости, и вся жидкость представляет собой поле вектора скорости.

Течение жидкости устанавливается или стационарное, если в каждой точке не зависит от времени

может меняться вдоль траектории, но в данной точке пространства скорость движения всех последующих проходящих частиц жидкости одинаковы.

Течение жидкости ламинарное, если слои жидкости движутся бес перемешивания.

Турбулентное - происходит перемешивание, из-за образования завихрений.

Число ламинарное, если число Рейнольда меньше критического.

Для круглых труб: ; d-диаметр

-средняя скорость течения

-динамический коэффициент вязкости

Линии тока - это линии в поле вектора скорости, касательные к-рым в каждой точке совпадает с направлением вектора скорости частиц.

По густоте линий тока, т.е. их число на единицу площади поверхности перпендикулярна к линиям тока, судят о скорости движения жидкости, где больше густота, там болше скорость частиц. Труба тока – часть жидкости, ограниченная линиями тока. Часть жидкости при движении не пересекает станок трубки тока, т.к. касат. в каждой точке к линиям тока, будет касат. и к поверхности трубки тока.

 

37^о. Уравнение неразрывности струи. Уравнение Бернулли

Рассм. сужающуюся струю (трубку тока)

Пусть 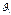частиц жидкости в сечении , а в сечении скорость .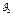

Через сечение за 1 сек пройдёт V жидкости 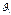= V₁, через сеч. объёмом: 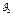, по заон сохранения масс имеем ,

= , жидкость слабосжимаемая.

,

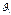
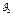Произведение скорости несжимаемой жидкости на поперечное сечение трубки, есть величина постоянная для данной трубки. Приходим к уравнению неразрывной несжимаемой жидкости: секундный объёмный (массовый) расход несжимаемой жидкости постоянен вдоль трубки тока. Из сказанного вытекает, что в местах, где трубка уже жидкость течёт быстрее, а где шире –течёт медленнее.

Получим уравнение Бернулли:

Рассм. малый объём жидкости в положении 1

Через время t этот объём перейдёт в положение

В силу равнения неразрывности:

Энергия каждой частицы жидкости складывается из кинетической и потенциальной:

Масса объёмов 1 и 2:

Тогда при перемещении объёмов жидкости из положения 1 в положение 2 приращение полной механической энергии будет =:

Т.к. жидкость идеальная (нет трения), то приращение энергий объёмов жидкости = разности работ сил давления, приложенных к сечениям и , при этом силы давления на боковые поверхности перпендикулярно перемещению и работы не совершают, имеем:

В силу закона сохранения:

Приравняем (1) и (2), сокращая на ур-ние Бернулли:

-динамическое давление или скоростной напор – дельная кинетическая энергия(энергия на единицу объёма)

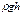-гидростатическое давление или гидравлический напор - дельная потенц. энергия в поле тяжести.

P- статическое давление, т.е. удельная энергия сил давления жидкости

Па=

Полный напор движущейся жидкости складывается из статического, гидравлического и скоростного напоров и остаётся постоянным при движении(g=0).

Из последнего выражения вытекает: «Там, где больше скорость потока, происходит уменьшение статического давления».

 

38 – 45

 

⇐ Предыдущая123456Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: