 |
Теплоемкость многоатомных газов.
|
|
|
|
 Числом степеней свободы i- назыв-ся число независимых параметров координат, характеризующих состояние системы. Молекулу одноатомного газа можно рассматривать как материальную точку, положение которой хар-ся тремя координатами: одноатомный газ (He): i=3 (x,y.z). Молекулы двухатомного газа(
Числом степеней свободы i- назыв-ся число независимых параметров координат, характеризующих состояние системы. Молекулу одноатомного газа можно рассматривать как материальную точку, положение которой хар-ся тремя координатами: одноатомный газ (He): i=3 (x,y.z). Молекулы двухатомного газа( ) можнр рассматрив. как систему 2-ух материальных точек с жесткой связью.
) можнр рассматрив. как систему 2-ух материальных точек с жесткой связью.
Трехатомный газ (C 
 i = 3+3+3-1-1-1=6
i = 3+3+3-1-1-1=6
Если связи молекул нежесткие, то необходимо учитывать и колебательн. степени свободы. Число степеней свободы i равно сумме чисел степеней свободы поступательного движения, вращательн. Движения и удвоенного числа степеней колебательного движения:
i= 
Средняя кинетич. энергия идеального одноатомного газа с числом степеней свободы i=3 равна:

Т.к. все степени свободы равноправны, то на одну степень свободы приходится энергия=  . Тогда приходим к закону о равном распределении энергии по степеням свободы. Для системы в термодин. Равновесии на каждую степень свободы приходится Е=
. Тогда приходим к закону о равном распределении энергии по степеням свободы. Для системы в термодин. Равновесии на каждую степень свободы приходится Е=  Тогда для молекулы многоатомного газа с числом степени свободы i: Е=
Тогда для молекулы многоатомного газа с числом степени свободы i: Е= 
Найдем внутрен. энергию одного моля идеалього газа:

 ;
; 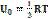 ; U=
; U=  RT
RT
Теплоемкость тела - кол-во теплоты, которую надо сообщить телу, чтобы нагреть его на 1 К (кельвин)

Молярная теплоемкость-кол-во теплоты, которую надо сообщить или отнять от одного моля в-ва, чтобы нагреть или охладить его на 1К. ) 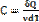 ; [ C]=
; [ C]= 
Удельная теплоемкость- кол-во теплоты, которую надо сообщить 1кг в-ва, чтобы нагреть его на 1К. 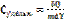 [
[ 
δQ= 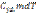 ; Q=
; Q= 
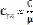
Теплоемкость в-ва зависит от вида протекающего процесса. В газе различают теплоемкость при постоянном объеме и постоянном давлении. (
δQ=dU+pdV; 
ν=1, V=const, dV=0  ; d
; d  ;
;
 ;
; 
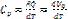 +
+  ; pV=RT
; pV=RT
p=const; pdV=RdT
 ;
; 
 - ф-ла Майера
- ф-ла Майера
|
|
|

 - показатель адиабаты.
- показатель адиабаты.
Мы рассмотрели классическую теорию теплоемкости: теплоемкости не зависят от температуры. Однако при низких температ. важную роль начинают играть квантовые эффекты (происходит замораживание вращат. и колебат. степней свободы и появляется зависимость теплоемкости от температуры).
Применение I начала термодинамики к изопроцессам(термодинамическим процессам).
Изопоцесс – термодинамич. проц.,при кот. один из параметров остается постоянным.
T=const – изотермическ., p=const – изобарн.,
V = const – изохорн.,
δQ = const – изэнтропический
1) T = const
δQ = dU+δA; dU =  VdT = 0
VdT = 0
δQ= δA все тепло,сообщенное сист. в изотермическом проц. идет на работу
δA=pdV
p= 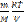 ; δA=
; δA= 
Проинтегрируем обе части ур-я от сост. V1 к V2
A12=  ; A12=
; A12= 
2) p=const
δQ=dU+ pdV тепло сообщ. сист. в изобарн. проц. идет на измен. внутрен. энергии и на работу сист.
Работа в изобарном проц.:
δA=pdV
A12=p  ; A12=p(V2-V1); A12=p∆V
; A12=p(V2-V1); A12=p∆V
d|| pV=  возьмем дифференциал
возьмем дифференциал
pdV=  ; δA=
; δA= 
Проинтегрируем:
A =  ; A =
; A = 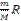 (T2-T1); A =
(T2-T1); A = 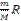 ∆T
∆T
ν =  = 1моль
= 1моль
 R =
R =  физический смысл: универсальная газовая постоян. R численно равна работе 1 моля идеального газа при изобарном нагревании его на 1 К.
физический смысл: универсальная газовая постоян. R численно равна работе 1 моля идеального газа при изобарном нагревании его на 1 К.
3) V=const
 δQ=dU
δQ=dU
δA=pdV=0 тепло сообщ. сист. в изохорн. проц. идет на увелич. внутр. энерг. сист.
Адиабатический процесс.
Адиабатич. – проц., протекающ. в сист. без теплообмена с окруж. средой. δQ=0
На практике адиабатическ. явл. быстро протекающ. проц.,не успевающ. установить теплообм. с окр. средой. I НТД(начало термодинамики) для адиабатич. проц.: dU+ δA=0
δA= -dU работа газа в адиабатном проц. соверш. тока за счет внутр. энерг. газа.
Получим ур-ние адиабаты, исходя из I НТД:
dU+ δA = 0
 VdT+ pdV = 0; p =
VdT+ pdV = 0; p = 
 VdT +
VdT +  = 0 ||
= 0 || 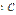 VT;
VT;  +
+ 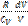 = 0
= 0
Интегрир. обе части последн. ур-ния:
 +
+ 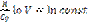

R=Cp-CV формула Майера

γ =  ;
; 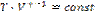
Получим теперь уравнение адиабаты впеременных p и V для идеального газа:
 pV=
pV= 
T= 
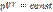
На диаграмме p и V адиабата идет круче,чем изотерма. Получим выраж. для работы в адиабатном проц.:
|
|
|
δA= -dU; δA= -  VdT
VdT
A=  ; A=
; A=  V (T1-T2)
V (T1-T2)
Политропный процесс
Политропный – процесс,протекающ. при постоян. теплоемкости. C=const.
Получим ур-ние полинтропы для идеального газа: I НТД имеет вид:
δQ=dU+δA
ν= 1 моль
δQ=CdT; C=  ; dU=
; dU=  VdT; δA=pdV
VdT; δA=pdV
CdT=  VdT+ pdV; (C-
VdT+ pdV; (C-  V )dT= pdV
V )dT= pdV
Воспользуемся тем, что газ идеальный: Ур-ние сост. идеального газа для 1 моля:
d|| pV=RT; pdV+Vdp=RdT
dT= 
(C-  V )
V )  ) = pRdV
) = pRdV
(C-  V –R)pdV+(C-
V –R)pdV+(C-  V )
V )  =0 ||: p(C-
=0 ||: p(C-  V )V
V )V

Проинтегрируем:
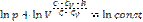
Потенцируя (обр. операц. логарифмиров.)
 =const; Cp=CV+R;
=const; Cp=CV+R;  =const
=const
Введем индекс политропы:
n = 
 ур-ние политропы
ур-ние политропы
Политропный проц. включ. в себя как частн. случаи все виды изопроц.
| n | Вид изопроцесса | С вид теплоемкости |
| p=const изобарный | Cp | |
| pV=const изотермичский | C 
| |
| γ |  адиабатный адиабатный
| |

| V=const изохорный | CV |
Изобразим изопроцессы на плоскости p и V

|
|
|


