 |
Модуль Юнга. Скорость звука.
|
|
|
|
Скорость звука.
Рассм. стержень длиной 
и площадью поперечного сечения S.
Δl =l- – абсол. деформация
ε= 
-относит-ая деформ-ия.
σ = 
- напрняжение
З-н Гука: Напряжение, прилож-ое к стрежню пропорционально относительному удлинению
σ = Eε – з-н Гука
Е – коэфф-т пропорциональности - модуль Юнга. – численно равен напряжению при относительной деыы-ции = 1: Е = σ/ε = 1
[E]= Па= 
Для твёрдых кристалл-их тел з-н Гука запис-тся с учётом того,что напряжение и отн-ая деформ-ция представляет собой тензоры
= │ 
│
= │ 
│
З-н Гука тогда приобретает вид: i. j. k. l = 1,2,3
= 
Найдём скорость распространения звука в сре 
де. Пусть вдоль однородного изотропного стержня вдоль оси x распростр-ся плоская одномерная продольная волна из-за деформации сжатия (растяж.)
Пусть вначале стержня часть среды смещается на величину dl за время dt, тогда dl = Udt (1)
За время dt возмущение распространяется со скоростью dv: l = vdt (2)
Т.к. волново дижение захватит расстояние l, то относительная деформация стержня:
По з-ну Гука:σ=Eε (4)
σ= 
Из (4) с учётом (5) и (3) имеем: F=SE 
(6)
По 2 з. Ньютона: 
(7)
Масса в-ва, вовлечённое в волновое движение: m = ρSl = ρSdt (8)
Т.к скорость колеблющихся частиц = U, то изменение импульса участка l: dp = mU = ρSVdtU F= 
= 
=ρSVU (10).
(6)=(10): ρSVU=SE 
; ρV= 
= 
; 
= 
= 
= 
; 
= 
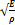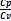
Механический принцип относительности, преобразования Галилео.
Инерциальными наз. сис-мы отсчёта, в кот-ых свободные тела движутся прямолинейно, равномерно или покоятся.
Мех-ий принцип отностительности был установлен Галилеем в 1630.
1. Формулировка: Все мех-ие явления во всех инерциальных системах отсчёта происходят совершенно одинаково.
2. Никакими мх-ими опытами, проведёнными внутри системы нельзя установить: находятся ли инерциальные сис-мы отсчёта в состоянии покоя или равномерно движения: Е = m*c2.
|
|
|
3. Современная форм-ка. Рассмотрим 2-е инерциальные системы S и S’ и пусть штрихован-ная система S’ движет-ся относительно не штрихованной S с постоянной V = const.
Пусть координаты т.М будет равны в S: x, y, z, t; S’: x’, y’, z’, t’.
Ф-лы преобразования координат при переходе от одной системы к другой, очевидно, имеет вид:
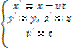(1)
Время t’=t течёт во все классической механике одинаково. Продифференцируем по времени с учётом dt=dt’
= 
= 
– V= 
- V
= 
= 
– V= 
(2)
= 
= 
– V= 
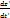- V
ф-лы (2) вытекает:
(3)
Из ф-лы (3) вытекает теория о сложении скоростей в классич. Механике:
Продифференцируем соотношение (2) ещё раз по времени. 
(4)
(5)
=
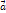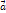
Т. Е. скорости в инерциальной системе отсчёта относительны, а ускорения-абсолютны.
Рассмотрим 2-ой з-н 1Ньютона в S и S’, то:
m ’=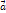 
’
m =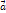
Массы в классической механике не меняются.
Силы и 
определяются только взаимным расположением тел с их скоростями, поэтому не зависят от выбора инерциальной системы отсчёта: =
Основное уравнение динамики m 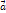= одинаково (неизменно) по форме при переходе от одной инерциальной системы отсчёта к другой. Тогда движение тела протекает одинаково во всех инерциальных системах отсчёта.
Формулировка: основное уравнение механики Ньютона инвариантно(неизменно) по форме относительно преобразований Галилея.
Постулаты СТО. Преобразование
Лоренца.
При движении тел сравнимых с движением света, преобразования Галилея оказываются неприменимыми. Движение близкое или равное к движению света описывается релятивистской механикой или теорией относительности.
В основе СТО лежат 3=2 основных постулата:
1.Принцип относительности Энштейна. Никакими опытами, в том числе и оптическими, нельзя установить движется ли данная инерциальная система отсчёта или покоится, т. е. все физические явления протекают одинаково во всех ИСО.
|
|
|
2.Опостоянстве скорости света. υ света в вакууме одинакова во всех ИСО и не зависит от движения приёмников и источников света.
Получим теперь преобразования Лоренца: пусть система S и S’связаны.
П усть S’ движется с постоянной 
, будем искать связь координат S и S’ относительно точки М:
x’ = γ(x-Vt) (1)
x = γ(x+Vt) (2)
γ-одинаков в (1) и (2) ввиду равноправности систем отсчёта.
Из (1) и(2) после преобразований можно получить: t = γ(t’+ 
(1- 
)) (3)
Коэффициет γ найдём из 2-ого постулата теории относительности. Рассмотрим распространение фронта светового сигнала, начавшего своё движение в S и S’, когда начало координат совпадали с системой S и S’. Пусть координаты сигнала в момент времени 
есть 
, а в момент времени 
есть .
остулату имеем:
= c (4); =c 
(5)
сь по 2-ому постулату с постоянна. Подставим (4) и (5) в соотношение (1) и (2), то получим:
; 
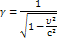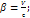γ = 
Если (6) подставить в (1), получим:
(7) 
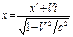(8)
Подставим (6) в (3), то:
(9); 
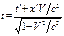(10)
Пр иходим к преобразованиям Лоренца:
(*)
Обратные преобразования Лоренца:
(**)
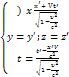Из преобр-ий (*) и (**) вытекает, что пространство и время взаимосвязаны. Из преобразований Лоренца в частности получ. преобразования Галилея
→ 0; 
; t’ = t
Были открыты преобр-я Кэрролла, которые нарушают принцип причинности:
x’ = x; t’ = t - 
|
|
|
