Основы метода симметричных составляющих

Метод симметричных составляющих является одним из основных методов, применяемых для расчета несимметричных режимов в линейных электрических системах. В его основе лежит возможность представления несимметричной системы ЭДС, напряжений или токов суммой трех симметричных систем и замена по принципу наложения расчета несимметричного режима работы трехфазной цепи расчетом трех симметричных режимов. Метод широко используется в релейной защите для расчета токов коротких замыканий в электрических сетях.

В соответствии с методом симметричных составляющих любую несимметричную трехфазную систему ЭДС, напряжений или токов можно представить суммой трех симметричных трехфазных систем: прямой, обратной и нулевой последовательности. Эти системы называют симметричными составляющими данной несимметричной трехфазной системы.

Например, несимметричную трехфазную систему напряжений (рисунок 2.11) можно заменить суммой трех симметричных систем:

1) системы напряжений прямой последовательности (трехфазной системы, в которой напряжения равны по амплитуде, сдвинуты по фазе на 120 градусов, с прямым чередованием фаз А, В, С);

2) системы напряжений обратной последовательности (трехфазной системы, в которой напряжения равны по амплитуде, сдвинуты по фазе на 120 градусов, с обратным чередованием фаз А, С, В);

3) системы напряжений нулевой последовательности (трехфазной системы, в которой напряжения равны по амплитуде и совпадают по фазе).

 

 

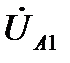
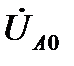
1) 2) 3)

Рисунок 2.11

Системы прямой и обратной последовательности являются уравновешенными, то есть сумма векторов трех фаз равна нулю. Система нулевой последовательности – неуравновешенная, сумма векторов равна утроенному значению одного вектора. Напряжения исходной системы будут определяться как сумма соответствующих симметричных составляющих

. (2.24)

Для более компактной записи (2.24) используют оператор фазы (или фазный множитель) .

Это такой вектор, скалярная величина которого равна 1 и который в комплексной плоскости образует с положительной осью вещественных чисел угол 120°. Умножить вектор на оператор фазы – значит повернуть его на 120° против часовой стрелки, не изменив величины (рисунок 2.12).

Рисунок 2.12 При этом, как и для любой симметричной системы векторов, справедливо равенство: .

Используя оператор фазы, напряжения систем прямой и обратной последовательностей для фаз В и С можно выразить через напряжения фазы А (индекс фазы А в дальнейшем опустим для упрощения записи)

В системе нулевой последовательности все напряжения имеют одинаковую фазу, поэтому .

С учетом этого выражения (2.24) перепишутся следующим образом

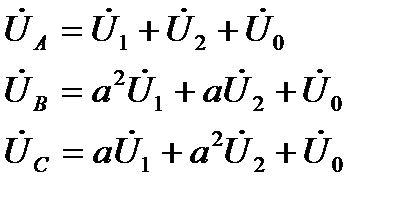. (2.25)

Это и будут основные выражения, которые мы будем дальше использовать для расчета несимметричных напряжений (токов, ЭДС), если известны их симметричные составляющие.

Если же предположить, что наоборот известны , а нужно найти симметричные составляющие , то, решая систему (2.25) относительно них, получим выражения для расчета симметричных составляющих:

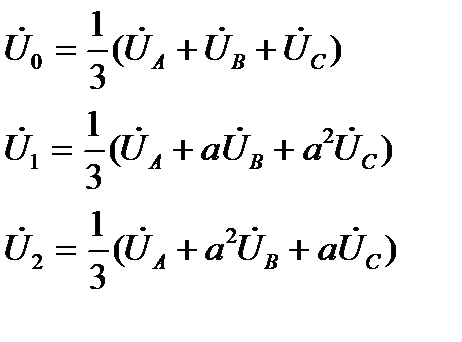. (2.26)

Аналогичные выражения получаются и для расчета симметричных составляющих токов и ЭДС.

Для более компактной записи преобразований метода симметричных составляющих удобно применять так называемую матрицу Фортескью (Фортескью – основоположник метода симметричных составляющих)

 

. (2.27)

Например, с помощью матрицы Фортескью уравнения (2.25) для расчета через симметричные составляющие запишутся следующим образом

(2.28)

или в матричной форме: .

При разложении заданной системы несимметричных векторов на симметричные составляющие (уравнения (2.26)) используют обращенную матрицу Фортескью , то есть .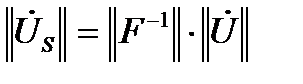

Преобразование векторов с использованием матрицы Фортескью целесообразно при расчетах в системе MathCad, так как это позволяет не расписывать отдельные формулы для расчета токов и напряжений.

⇐ Предыдущая12345678Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: