 |
Мощность при несинусоидальных напряжениях и токах
|
|
|
|
Под активной мощностью (Р, Вт) несинусоидального тока понимают среднее значение мгновенной мощности за период первой гармоники:
 . (2.46)
. (2.46)
Если представить напряжение  и ток
и ток 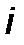 рядами Фурье
рядами Фурье
 ;
;

и подставить эти ряды в выражение (22), то можно получить:
 , (2.47)
, (2.47)
где  - угол между
- угол между  и
и  .
.
Таким образом, активная мощность несинусоидального тока равна сумме активных мощностей отдельных гармоник.
Аналогично выводится понятие реактивной мощности (Q, ВАр):
 . (2.48)
. (2.48)
Полная мощность ( S, ВА) равна произведению действующего значения несинусоидального напряжения на действующее значение несинусоидального тока:
 , (2.49)
, (2.49)
где  ;
;  .
.
В цепях c несинусоидальными токами в отличие от синусоидальных цепей
 ;
;  , (2.50)
, (2.50)
так как в них действует мощность искажения (Т, ВАр), обусловленная наличием высших гармоник;
 . (2.51)
. (2.51)
Отношение активной мощности к полной называется коэффициентом мощности.
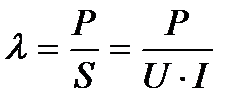 . (2.52)
. (2.52)
Для синусоидальных цепей  , но в несинусоидальных цепях появляется коэффициент искажения
, но в несинусоидальных цепях появляется коэффициент искажения 

Пример решения задачи 3
Проведем расчет линейной электрической цепи. Схема и кривая несинусоидальной ЭДС приложенной к цепи показаны на рисунке 2.23.
Рисунок 2.23
Значения параметров:
 Ом;
Ом;  Ом;
Ом; 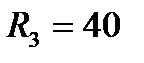 Ом;
Ом;  с;
с;
 мГн;
мГн;  мГн;
мГн;  мкФ;
мкФ;  В;
В;
Представим ЭДС источника, заданную графически, рядом Фурье, ограничив число членов ряда постоянной составляющей и тремя первыми значимыми гармоническими составляющими:
 , В.
, В.
Построим графики спектров амплитуд и начальных фаз ЭДС источника, рисунок 2.24.
а) АЧХ (амплитудо-частотная характеристика б) ФЧХ (фазо-частотная характеристика)
Рисунок 2.24
Приближенное действующее значение ЭДС:
 В.
В.
На рисунке 2.25 показана заданная кривая несинусоидальной ЭДС и кривая, полученная в результате сложения постоянной составляющей и первых трёх гармонических составляющих ряда. Построение осуществлено в среде MathCad.
|
|
|

|
Рисунок 2.25
На рисунке 2.25

|

|

|

|

|

|
Расчёт токов в ветвях проводим для каждой составляющей спектра по отдельности:
а) постоянная составляющая (учтём, что для постоянного тока идеальный индуктивный элемент – это короткозамкнутая перемычка, а идеальный емкостной элемент – разрыв цепи):
 В,
В,
 А,
А,
 ,
,
 Вт,
Вт,
 Вт.
Вт.
б) первая (основная) гармоническая составляющая:
 , В,
, В,
перейдем к комплексному амплитудному значению ЭДС:
 , В.
, В.
Комплексные сопротивления ветвей:
 Ом,
Ом,
 Ом,
Ом,
 Ом,
Ом,
 Ом.
Ом.
Комплексные амплитуды токов ветвей на первой гармонике:
 А,
А,
 В,
В,
 А,
А,
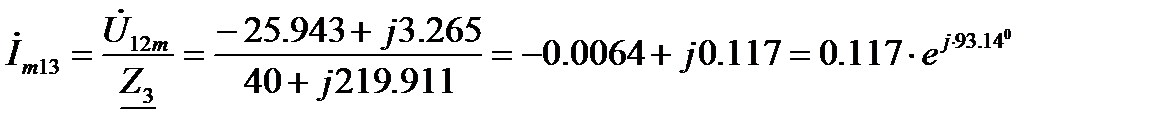 А.
А.
Мгновенные значения токов в ветвях на первой гармонике:
 А,
А,
 А,
А,
 А.
А.
Баланс мощностей:
 ВА,
ВА,
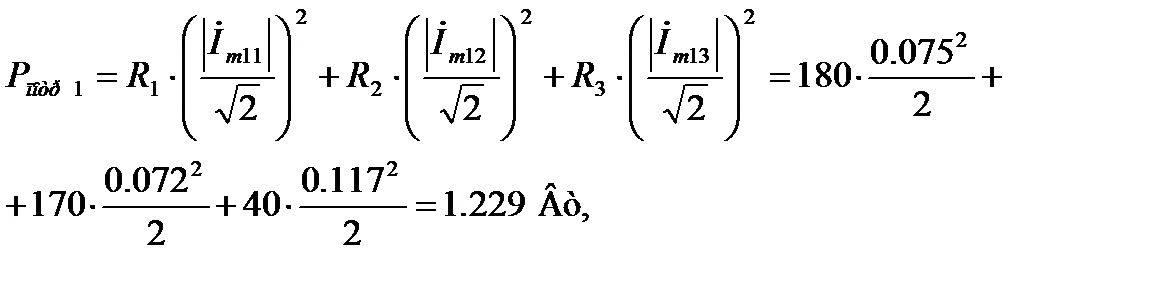

Векторная диаграмма токов на первой гармонике:
Рисунок 2.26
в) вторая гармоническая составляющая:
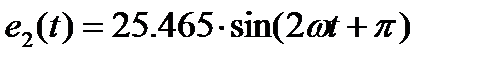 , В,
, В,
перейдем к комплексному амплитудному значению ЭДС:
 , В.
, В.
Комплексные сопротивления ветвей:
 Ом,
Ом,
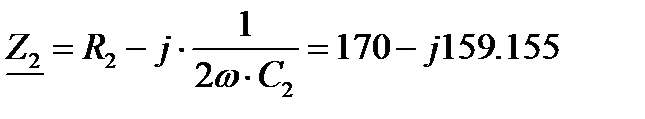 Ом,
Ом,
 Ом,
Ом,
 Ом.
Ом.
Комплексные амплитуды токов ветвей на второй гармонике:
 А,
А,
 В,
В,
 А,
А,
 А.
А.
Мгновенные значения токов в ветвях на второй гармонике:
 А,
А,
 А,
А,
 А.
А.
Баланс мощностей
 ВА,
ВА,


Векторная диаграмма токов на второй гармонике:
Рисунок 2.27
г) третья гармоническая составляющая:
 , В,
, В,
перейдем к комплексному амплитудному значению ЭДС:
 , В.
, В.
Комплексные сопротивления ветвей:
 Ом,
Ом,  Ом,
Ом,
 Ом,
Ом,  Ом.
Ом.
Комплексные амплитуды токов ветвей на третьей гармонике:
 А,
А,
 В,
В,
 А,
А,
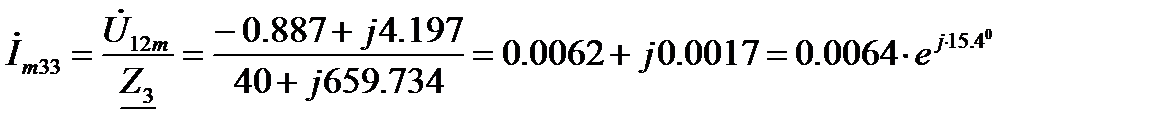 А.
А.
Мгновенные значения токов в ветвях на третьей гармонике:
 А,
А,  А,
А,
 А.
А.
Баланс мощностей
 ВА,
ВА,


Векторная диаграмма токов на третьей гармонике:
Рисунок 2.28
Используя метод наложения, запишем мгновенные токи ветвей:
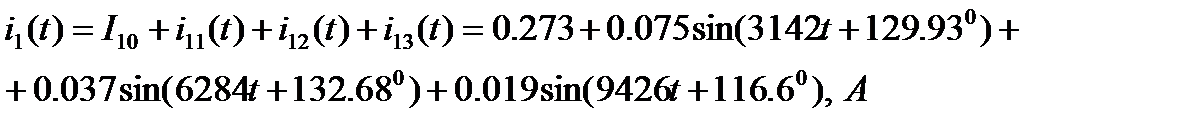


Действующие значения токов ветвей:
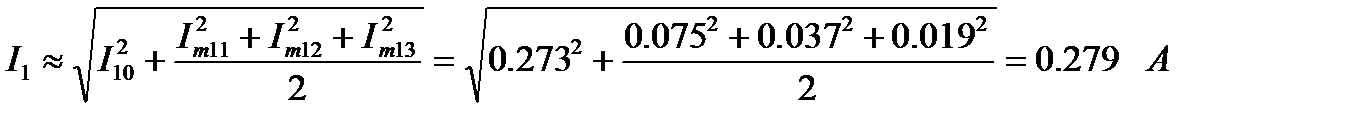 ,
,
 ,
,
 .
.
Для определения мощности искажения определим полную мощность, активную и реактивную мощности всей цепи.
|
|
|
Полная мощность
 ВА;
ВА;
Активная мощность
 Вт;
Вт;
Реактивная мощность
 вар;
вар;
Мощность искажения
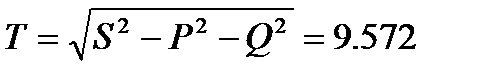 вар;
вар;
Коэффициент мощности


|
|
|


