 |
Определение постоянных интегрирования
|
|
|
|
Постоянные интегрирования, входящие в выражения для свободных составляющих, вычисляют, подставляя известные начальные условия в выражения для искомой функции и ее (n - 1) производных для момента времени t = 0+ (n – количество корней характеристического уравнения).
В самом общем случае, когда характеристическое уравнение имеет
n корней и решение для переходного тока или напряжения записывается в виде
, для нахождения постоянных интегрирования А1, А2,…… Аn нужно составить систему n уравнений следующего вида
. (2.56)
В этих уравнениях 
- значения принужденных составляющих для
t = 0+ , 
….. 
- значения производных принужденных составляющих для момента времени t = 0+. Они легко определяются по полученным выражениям для принужденных составляющих.
Если в задаче рассматривается переходной процесс в цепи постоянного тока, то 
, а все производные равны нулю: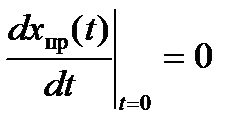 
; …. 
.
В цепи синусоидального тока принужденные составляющие изменяются тоже по синусоидальному закону 
, первая производная для них определяется выражением 
.
Для момента времени t = 0 
, 
.
В таблице 2.6 приведены выражения для переходных токов или напряжений и их первых производных для случая переходного процесса в цепи постоянного тока.
Уравнения для расчета постоянных интегрирования приведены в последнем столбце таблицы, они получаются, если в выражения переходной величины и первой производной подставить t = 0.
Таблица 2.6 - Уравнения для расчета постоянных интегрирования
| Выражения для переходных токов и напряжений | Необхо-димые началь-ные условия | Выражения первых производных для переходных токов и напряжений, используемые для расчета постоянных интегрирования | Уравнения для расчета постоянных интегрирования (при переходном процессе в цепи постоянного тока) |
|
| - |
|
|  ;
|
| 
|
| ;
|
| 
|
| ;
|
| 
|
|
|
|
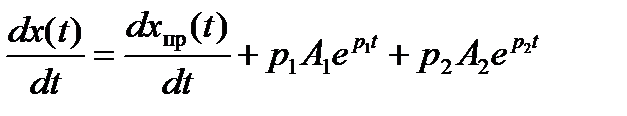
Начальные условия
Для определения постоянных интегрирования по формулам таблицы 2.6 необходимо предварительно рассчитать начальные условия.
Начальными условиями называются значения токов, напряжений и их производных в начальный момент переходного процесса, при 
.
Начальные условия делятся на независимые и зависимые.
Независимые начальные условия – это значения токов индуктивных элементов 
и напряжений емкостных элементов 
для времени
Независимые начальные условия определяются из законов коммутации. 
; 
.
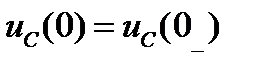Они могут быть нулевыми и ненулевыми.
Зависимые начальные условия – это значения всех остальных токов, напряжений и производных по времени токов и напряжений для времени . Зависимые начальные условия определяются:
- после того, как рассчитаны независимые начальные условия;
- из уравнений по законам Кирхгофа для послекоммутационной схемы, записанных для времени .
Количество начальных условий, которые нужно рассчитать равно количеству постоянных интегрирования в выражении переходной величины. Как следует из таблицы 2.6, если характеристическое уравнение имеет один корень и в выражение свободного тока или напряжения входит одна неизвестная постоянная интегрирования, для ее определения необходимо предварительно рассчитать только одно начальное условие: значение самой функции 
. Если неизвестных постоянных интегрирования – две, то для их определения предварительно рассчитывают два начальных условия: значение самой функции и ее первой производной 
для момента времени t = 0+ . Примеры расчета начальных условий приведены ниже.
Пример 1 (рисунок 2.35).
| E |
|
|
|
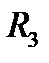
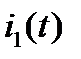
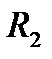
Е = 100 В, R1 = 10 Ом, R2 = 10 Ом,
R3 = 10 Ом, L = 0,1 Гн
Найти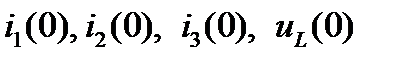 
Рисунок 2.35
Сначала найдем независимое начальное условие: для данной схемы – это
ток 
, так как это ток через индуктивность. По первому закону коммутации он будет равен току через эту же индуктивность в последний момент перед коммутацией.
| E |
До коммутации в цепи (рисунок 2.36) протекал один постоянный ток
Этот ток постоянный и от времени
не зависит, поэтому для времени 
Рисунок 2.36 
По первому закону коммутации 
Остальные искомые начальные значения токов токи и напряжения на индуктивности являются зависимыми начальными условиями.
Для их определения систему уравнений по законам Кирхгофа для схемы после коммутации запишем для момента времени .
.
Неизвестными в этих уравнениях являются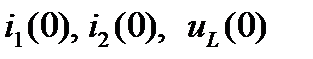 
. Их можно найти, решив составленную систему уравнений любым методом в Mathcad или вручную, например, с помощью подстановки.
Из первого уравнения выразим 
и подставим его во второе уравнение, получим 
.
Отсюда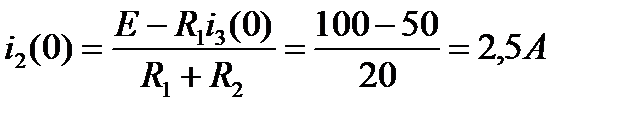 
;
С учетом этого 
; 
Пример 2 (рисунок 2.37)
Е = 100 В;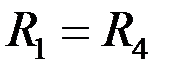 
= 10 Ом;
= 20 Ом; L = 0,05 Гн; С = 250 мкФ.
Найти 
, 
Рисунок 2.37
Из схемы до коммутации найдем независимые начальные условия (ток индуктивного и напряжение емкостного элементов для момента времени t = 0-). Поскольку в ветви с емкостным элементом при Е = const ток отсутствует, то: i 1(0) = i 3(0-) = E /(R 1 + R 3 + R 4) или i 1(0) = 100/(10 + 10 + 20) = 2,5 A,
uC (0) = i 3(0-) × R 3 = 2,5 × 20 = 50 B.
Для определения зависимых начальных условий записываем уравнения по законам Кирхгофа для схемы после коммутации для момента времени t = 0+:
. 
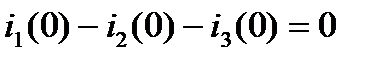
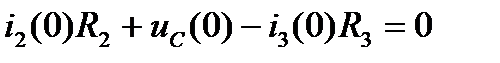Подставляя в эти уравнения найденные выше независимые начальные условия i 1(0) и uC (0), находим: 
A; 
A; 
B.
Производная тока через индуктивность находится из формулы 
, производная напряжения на емкости - из формулы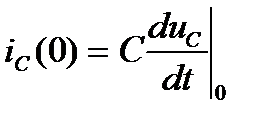 
.
|
|
|
