 |
Пример расчета цепи с поперечной несимметрией
|
|
|
|
Рассмотрим трехфазную цепь c симметричным генератором и симметричной нагрузкой, в которой произошло короткое замыкание фазы А на землю (рисунок 2.14).
|
|
 |
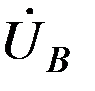
Рисунок 2.14
Известны фазная ЭДС генератора 
, фазные сопротивления прямой, обратной и нулевой последовательности для линии 
и нагрузки 
, сопротивление нейтрального провода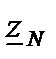 
. Требуется методом симметричных составляющих рассчитать токи и напряжения в месте короткого замыкания.
В соответствии с алгоритмом несимметричный участок в линии заменим эквивалентным источником с несимметричной системой напряжений 
(рисунок 2.15).
| A |
| B |
| C |
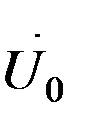
Рисунок 2.15
Системы трех несимметричных напряжений 
и трех несимметричных токов 
в месте несимметрии представим в виде суммы трех симметричных систем: прямой обратной и нулевой последовательности, симметричные составляющие которых 
и 
нужно определить.
По методу симметричных составляющих вместо исходной схемы нужно рассчитать три трехфазные схемы: прямой, обратной и нулевой последовательностей. Но так как режимы в каждой из этих схем будут симметричны, расчет проводится только для одной фазы. Обычно для расчета в качестве основной фазы выбирают фазу А, для сокращения записи индекс «А» у симметричных составляющих токов и напряжений для этой фазы не ставят.
Учитывая это, сразу составим три однофазные схемы замещения, которые и будем использовать для расчета, они показаны в первом столбце таблицы 2.4.
В схему прямой последовательности будут включены фазная ЭДС генератора и сопротивления всех элементов цепи прямой последовательности. Здесь 
и 
- симметричные составляющие напряжения и тока прямой последовательности в месте короткого замыкания.
|
|
|
Таблица 2.4
| Однофазные схемы замещения | Однофазные схемы замещения после преобразования до одного контура |
| Схема прямой последовательности | Схема прямой последовательности |
      
|   
|
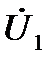
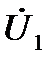
| Схема обратной последовательности | Схема обратной последовательности |
     
|   
|
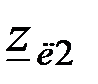
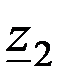
| Схема нулевой последовательности | Схема нулевой последовательности |
      
|   
|
Конфигурация схемы обратной последовательности будет такая же, но схема не будет содержать ЭДС (так как мы имеем симметричную систему ЭДС на входе). В ней будут включены сопротивления всех элементов цепи обратной последовательности, 
и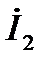 
- симметричные составляющие напряжения и тока обратной последовательности в месте короткого замыкания.
Конфигурация схемы нулевой последовательности в рассматриваемом примере будет отличаться от схемы обратной последовательности только наличием утроенного сопротивления нейтрального провода. В ней будут включены сопротивления всех элементов цепи нулевой последовательности, 
и 
- симметричные составляющие напряжения и тока нулевой последовательности в месте короткого замыкания.
Следует отметить, что в других случаях схема нулевой последовательности может существенно отличаться от схем прямой и обратной последовательностей. При ее составлении нужно учесть следующее:
1) если нагрузка не имеет нулевого провода (то есть соединена звездой без нулевого провода или треугольником), то ветви с сопротивлением нагрузки 
в схеме не будет;
2) если в схеме произошло междуфазное короткое замыкание, то схему нулевой последовательности вообще не составляют, так как ток и напряжение нулевой последовательности будут равны нулю. Поэтому для случая междуфазного к.з. составляют всего две схемы замещения: прямой и обратной последовательности.
|
|
|
После составления схем замещения преобразуем их к простейшему виду (одному контуру), сложив параллельные ветви относительно места короткого замыкания. Эквивалентную ЭДС 
и эквивалентные сопротивления 
найдем по известным формулам эквивалентных преобразований.Схемы после преобразования показаны в столбце 2 таблицы 2.4.
Для нахождения шести неизвестных симметричных составляющих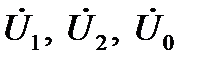 
и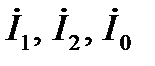 
составим систему из шести уравнений:
- первые три уравнения запишем для одноконтурных схем замещения (таблица 2.4) по второму закону Кирхгофа;
- остальные три уравнения запишем по условиям в месте несимметрии. (для рассматриваемого случая к.з. на землю фазы А граничные условия 
, выразим их через симметричные составляющие).
. (2.29)
Полученную систему линейных алгебраических уравнений (2.29) можно решать как на ЭВМ, например, в системе MathCad, так и вручную.
Для решения в MathCad составляется матрица коэффициентов и матрица свободных членов.
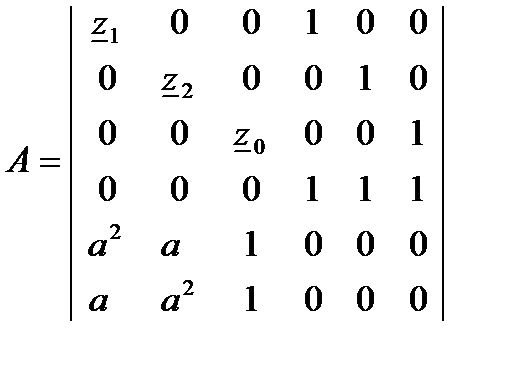
Далее решение системы идет по любому известному алгоритму, например, 
. В результате решения получим матрицу искомых симметричных составляющих
,
Зная симметричные составляющие, найдем токи и напряжения в месте короткого замыкания. Их можно найти, используя матрицу Фортескью (2.27) или выражения (2.25)
. (2.30)
Систему (2.29) очень просто можно решить и вручную, приведя ее к одному уравнению с одним неизвестным. Для этого все неизвестные величины нужно выразить через одну величину, например, ток 
. Покажем, как это сделать наиболее просто.
Сначала, используя формулы (2.26) для расчета симметричных составляющих и граничные условия для токов 
, установим зависимости между токами 
:
.
Отсюда сразу очевидно, что
. (2.31)
Далее сложим три первые уравнения системы (2.29), получим
.
С учетом (2.31) заменим токи 
на 
и учтем, что 
. Получим 
, откуда ток прямой последовательности будет находиться по формуле 
.
Остальные симметричные составляющие токов и напряжений найдутся по формулам 
, 
. Искомые токи и напряжения в месте короткого замыкания находятся по (2.30).
На рисунке 2,16 показаны примерные векторные диаграммы токов и напряжений прямой, обратной и нулевой последовательностей и векторные диаграммы результирующих токов и напряжений в месте короткого замыкания для рассмотренного случая однофазного короткого замыкания на землю.
|
|
|
Из векторных диаграмм видно, что ток фазы А в месте короткого замыкания 
равен сумме равных симметричных составляющих токов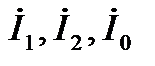 
, токи других фаз 
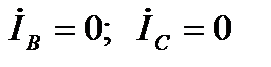. Напряжение между фазой А и землей 
, напряжения между фазами В и С и землей находятся как сумма соответствующих симметричных составляющих.
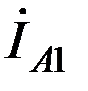
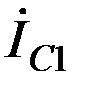
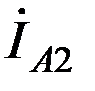
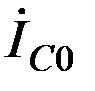
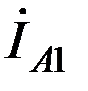
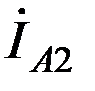
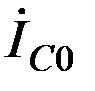
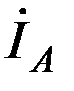
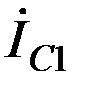
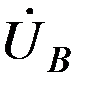
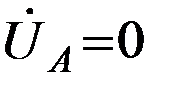
Рисунок 2.16
Если в задаче требуется найти еще токи в линии или нагрузке, то из схем замещения находятся сначала симметричные составляющие этих токов, а затем находятся сами токи.
При любых других видах поперечной несимметрии расчет будет аналогичным.
Для случая междуфазного короткого замыкания, при котором ток и напряжение нулевой последовательности 
и 
получаются равными нулю, с целью упрощения расчетов, как правило
- составляют всего две схемы замещения (прямой и обратной последовательности);
- составляют не шесть, а четыре уравнения: два – по второму закону Кирхгофа, два – по условиям в месте несимметрии. Неизвестными в этих уравнениях будут симметричные составляющие напряжений и токов прямой и обратной последовательности 
и 
.
Однако, нужно отметить, что при расчетах в MathCad можно предельно формализовать задачу и при любых видах поперечной несимметрии (в том числе и при междуфазном к.з.) составлять три схемы и шесть уравнений. Для случая междуфазного к.з и получатся равными нулю из решения этих шести уравнений.
|
|
|
