 |
Тема: Линейная функция и ее график
|
|
|
|
Цели: - познакомить учащихся с линейной функцией и ее графиком;
развивать математическую речь, активность, внимание, навыки
самостоятельности;
воспитывать аккуратность, интерес к предмету.
Оборудование: портрет Пьера Ферма.
Ход урока:
1. Сообщение темы и целей урока.
2. Работа по теме урока.
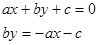
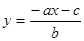
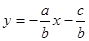
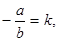
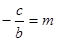
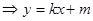
Линейное уравнение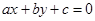 
с 2 переменными 
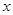и 
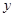всегда можно преобразовать к виду 
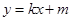, где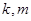 
-числа (коэффициенты), причем 
.
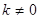Этот частный вид линейного уравнения будем называть линейной функцией.
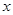-независимая переменная (или аргумент), 
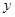-зависимая переменная.
Линейная функция - это специальный вид линейного уравнения с 2 переменными.
Графиком линейной функции 
является прямая.
3. Исторический экскурс о Пьере Ферма.
Пьер Ферма (1601-1665)
В истории математики Пьер Ферма занимает особое место. Он известен как автор "великой теоремы Ферма", которая чрезвычайно просто формулируется и которую до сих пор еще не удалось доказать.
Сумма квадратов двух целых чисел снова может быть квадратом целого числа. Например, 52+122=132. Теорема Ферма утверждает, что для более высоких степеней подобное невозможно, т.е. уравнение х n+ yn= zn не имеет решений в целых числах ни при каких n > 2.
Сотни квалифицированных математиков и тысячи дилетантов в течение трехсот лет пытались доказать эту теорему. В 1993 году на страницах многих газет, не склонных писать о математике, промелькнула сенсационная новость: теорема наконец-то доказана! Но вскоре, как бывало уже не раз, в доказательстве обнаружилась ошибка.
Ферма вошел в славную когорту "обыкновенных гениев" начала XVII века, вместе с Декартом, Паскалем, Гюйгенсом… Но, справедливости ради, надо отметить, что именно его долгое время считали сильнейшим математиком века - вплоть до появления работ Ньютона и Лейбница.
|
|
|
Как и Декарт, Пьер Ферма родился на юге Франции, получил всестороннее образование - не только естественнонаучное, но и гуманитарное. Большую часть жизни он проработал юристом в парламенте города Тулузы. Хотя в то время математика уже была уважаемой наукой, но еще не считалась профессией.
Научных журналов тоже еще не существовало (первый из них появился в год смерти Ферма). Поэтому математики обменивались сведениями о своих достижениях в личной переписке. В истории науки вошло имя парижского священника Мерсенна, сыгравшего роль информационного центра для математиков разных стран. Сообщить о своем открытии Мерсенну означало опубликовать его для всей Европы.
В 1636 году Ферма отправил Мерсенну письмо, в котором изложил свой метод решения задач о максимуме и минимуме. Мерсенн переслал копию этого письма другим математикам, в том числе Декарту. Рассуждения Ферма, использующие бесконечно малые величины, показались Декарту недостаточно ясными, и он подверг работу младшего коллеги резкой критике. Так через две тысячи лет после работ Архимеда возобновились споры о законности действий с бесконечно малыми величинами, не утихавшие до XIX столетия.
Одновременно с Декартом Ферма пришел к созданию аналитической геометрии - науки, описывающей геометрические фигуры при помощи координат и формул. Однако Ферма пользовался неудобными обозначениями и не претендовал на открытие "универсальной математики", поэтому его рукопись была менее известна, чем "Геометрия" Декарта.
Ферма был одним из отцов теории вероятностей - современной науки, без которой невозможна работа страховых компаний или расчеты мощностей телефонных станций. Поводом для его исследований были азартные игры, особенно игра в кости, весьма распространенная в то время.
|
|
|
Помимо всего этого, Ферма оказался единственным математиком XVII века, занимавшимся арифметикой. Именно с его работ начинается современная теория чисел. Настольной книгой Ферма стала "Арифметика" древнегреческого математика Диофанта.
Самостоятельная работа учащихся: подготовить сообщениео Паскале.
4. Закрепление полученных знаний.
4.1 Выполнение № 897 (у доски):
а) Заданный промежуток является интервалом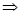 
наибольшего и наименьшего значений не существует.
б) Функция убывает 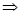наибольшее значение в начале промежутка, а наименьшее в конце. Но в конце промежутка стоит знак +∞ 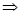наименьшего значения не существует.
Наибольшее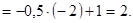 
в) Функция возрастает 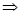наименьшее значение в начале промежутка, а наибольшее в конце.
Наименьшее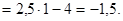 
Наибольшее =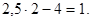 
г) Функция возрастает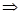 
наименьшее значение в начале промежутка, а наибольшее в конце.
Но в начале промежутка стоит знак - ∞ 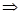наименьшего значения не существует.
Наибольшее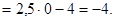 
4.2 Выполнение № 898 (а) (у доски):
а) Функция возрастает 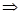наименьшее значение в начале промежутка, а а наибольшее в конце.
Наименьшее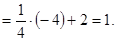 
Наибольшее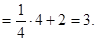 
4.3 Выполнение № 863 (г) (у доски):
г)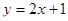 
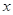
| -1 | 0 | 1 |
| -1 | 1 | 3 |
4.4 Выполнение № 855 (б) (с комментированием):
б)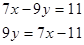 
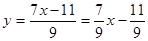
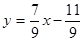
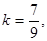
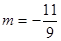
4.5 Выполнение № 851 (а) (с комментированием):
а)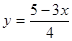 
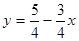
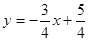
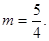
5. Д/з № 868 (в), № 876, № 888 (в, г).
6. Итог урока.
Анализ урока.
Тип урока - урок изучения нового материала. Цели и задачи урока: познакомить учащихся с линейной функцией и ее графиком; развивать математическую речь, активность, внимание, навыки самостоятельности; воспитывать аккуратность, интерес к предмету. Цели и задачи урока решены. Исторический экскурс о Пьере Ферма. В качестве дополнительного домашнего задания учащимся была предложена самостоятельная работа. Исторический материал заинтересовал учащихся.
В разное время ученые и методисты по-разному определяли цели введения элементов истории математики в преподавание в зависимости от общих задач школы. Однако можно сформулировать общие цели для всех школ:
· повышение интереса учащихся к изучению математики и углубление понимания ими изучаемого фактического материала;
· расширение умственного кругозора учащихся;
|
|
|
· повышение общей культуры учащихся;
· умение работать с дополнительной литературой, справочниками, энциклопедиями.
В наше время юноша и девушка, оканчивающие среднюю школу, должны иметь представление о месте и роли математики в современной передовой культуре. Одно сообщение сведений по истории математики далеко не всегда способствует достижению общих целей, для всех школ. Знакомство учеников с историей математики означает продуманное планомерное использование на уроках фактов из истории науки и их тесное сплетение с систематическим изложением всего материала программы. Лишь такое сплетение может способствовать достижению указанных целей. Координируя изучение математики с другими предметами, в частности с историей, подчеркивая роль и влияние практики на развитие математики, указывая условия, а иногда и причины зарождения и развития тех или иных идей и методов, тем самым способствуем процессу их умственного созревания и сознательному усвоению ими учебного материала [18, 39].
Достигнутое таким образом более глубокое понимание школьного курса математики, безусловно, вызовет у учащихся рост интереса к предмету. Ознакомление учеников с историей математики должно проводиться в основном на уроках математики и лишь во вторую очередь на внеклассных занятиях. При этом не следует рассчитывать на какие-либо дополнительные часы. Залог успеха состоит в умелом использовании элементов истории математики таким образом, чтобы они органически сливались с излагаемым фактическим материалом. Большую методическую трудность представляет решение вопроса об отборе конкретного материала по истории математики и о порядке его использования в том или другом классе. Здесь следует руководствоваться программой по алгебре. Однако, учитывая возрастные особенности учащихся, нельзя приспосабливаться к программе. Не только содержание и объем, но и стиль изложения вопросов из истории математики не могут быть одинаковыми в разных классах. Трудным кажется на первый взгляд решение вопроса о том, как выкроить необходимое время. Однако вопрос о времени, как и вопрос о формах использования элементов истории математики на уроках, почти полностью подчинен главному вопросу - связи изучаемой в школе математики с ее историей. Какая бы ни была форма сообщения сведений по истории - каждая беседа, экскурс, лаконичная справка, решение задачи, показ и разъяснение рисунка, использованное время нельзя считать потерянным, если только учитель сумеет исторический факт преподнести в тесной связи с излагаемым на уроке теоретическим материалом. В результате такой связи у школьников пробудится повышенный интерес к предмету и тем самым повысится эффективность их знаний. Отчет работы педагогов подсказывает: следует широко использовать для ознакомления с историей математики уроки закрепления пройденного, что будет способствовать оживлению этих уроков [19, 33].
|
|
|
Таким образом, главную методическую трудность представляет вопрос о том, как на деле сочетать изучение определенного раздела программы алгебры с изложением соответствующего исторического материала. Преодолеть эту трудность можно лишь в ходе планомерной и скрупулезной работы.
|
|
|
