 |
И полная. Баланс мощностей
|
|
|
|
Мгновенной мощностью называют произведение мгновенного напряжения на входе цепи на мгновенный ток.
Пусть напряжение и ток являются синусоидальными функциями времени:
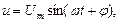
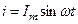(в данном случае при нулевой начальной фазе тока φ = ψu).
Получим выражение для мгновенной мощности:
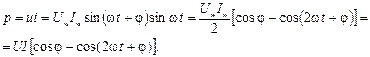
| (30) |
Из (30) следует, что мгновенная мощность изменяется с частотой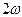 
, в два раза превышающей частоту тока и напряжения.
Среднее значение мгновенной мощности за период T называют активной мощностью и обозначают буквой P:
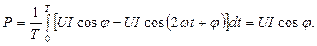
| (31) |
При выводе (31), учтено равенство:
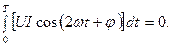
Учитывая, что из треугольника сопротивлений (см. рис. 15) следует соотношение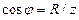 
и из треугольника проводимостей (см. рис. 16) 
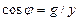, получаем из (31) следующие выражения для активной мощности:
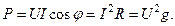
| (32) |
Активная мощность измеряется в ваттах (Вт) и характеризует необратимое преобразование электрической энергии, которая выделяется в виде теплоты на участках цепи в активных сопротивлениях. В электрических двигателях потребляемая из сети активная мощность преобразуется в механическую мощность (за вычетом потерь в процессе преобразования) и является их основной характеристикой.
Множитель cos φ называется коэффициентом мощности. Коэффициент мощности является одной из важнейших характеристик электротехнических устройств и повышение его до предельного значения cos φ = 1 является одной из основных задач энергосбережения.
Рассмотрим идеальные реактивные элементы (индуктивность и емкость). Активная мощность в этих элементах равна нулю, так как напряжение и ток в индуктивности или емкости различаются по фазе на 90o и cos φ = 0.
В реактивных элементах отсутствуют необратимые потери электрической энергии, не происходит нагрева элементов. Происходит обратимый процесс в виде обмена электрической энергией между источником и приемником. Для качественной оценки интенсивности обмена энергией вводится понятие реактивной мощности Q.
|
|
|
Преобразуем выражение (30) для мгновенной мощности:
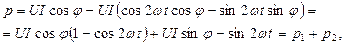
где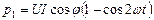 
– мгновенная мощность активного сопротивления; 
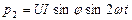– мгновенная мощность реактивного элемента (индуктивности или емкости).
Максимальное или амплитудное значение мощности p 2 называется реактивной мощностью:
| Q = UI sin φ = I 2 х = U 2 b, | (33) |
где x, b – соответственно реактивные сопротивление и проводимость.
Реактивная мощность измеряется в вольт-амперах реактивных (ВАр) и расходуется на создание магнитного поля в индуктивности или электрического поля в емкости. Энергия, накопленная в емкости или в индуктивности, периодически возвращается источнику питания.
Амплитудное значение суммарной мощности p = p 1 + p 2 называется полной мощностью. Полная мощность, измеряемая в вольт-амперах (В·А), равна произведению действующих значений напряжения и тока:
 .
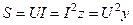| (34) |
| Возьмем треугольник сопротивлений (см. рис. 15) и умножим его стороны на квадрат тока в цепи. Получим подобный треугольник мощностей (рис. 17). | 
Рис. 17
|
Из треугольника мощностей получим соотношения между мощностями P, Q, S:
  ,   .
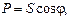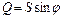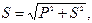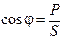| (35) |
При расчете электрических цепей комплексным методом используют выражение комплексной мощности, равное произведению комплексного напряжения на сопряженный комплекс тока. Для цепи, имеющей активно-индуктивный характер, ток по фазе отстает от напряжения на угол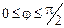 
:
,
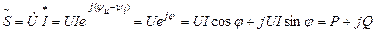где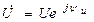 
– комплекс напряжения; 
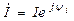– комплекс тока; 
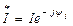– сопряженный комплекс тока; 
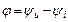– сдвиг по фазе между напряжением и током.
Вещественной частью полной комплексной мощности является активная мощность, мнимой частью комплексной мощности – реактивная мощность:
  .
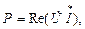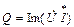| (36) |
Для цепи, имеющей активно-емкостной характер, ток по фазе опережает напряжение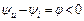 
.
|
|
|
.
Активная мощность всегда положительна. Реактивная мощность в цепи, имеющей индуктивный характер, – положительна, а в цепи с емкостным характером – отрицательна.
При выводе полученных соотношений предполагалось, что на зажимах цепи действует напряжение U. Если к зажимам цепи присоединен идеальный источник синусоидальной ЭДС с действующим значением E, то выражения (32) – (34), (36) для источника имеют следующий вид:
 ;   .
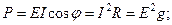
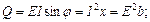
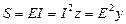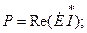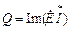| (37) |
Из закона сохранения энергии следует, что для электрической цепи соблюдается закон баланса активных мощностей: активная мощность, генерируемая источниками, равна активной мощности, потребляемой всеми приемниками.
Покажем, что соблюдается баланс и для комплексных, и, следовательно, для реактивных мощностей. Определим комплексные мощности для схемы (см. рис. 7), содержащей идеальный источник синусоидальной ЭДС, последовательно соединенные активные и реактивные сопротивления приемника.
Запишем уравнение по второму закону Кирхгофа, умножим левую и правую части уравнения на сопряженный комплекс тока и учтем свойства произведения комплексно сопряженных чисел:
, 
,
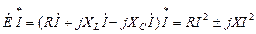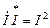где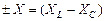 
– результирующее реактивное сопротивление.
,
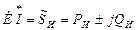где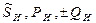 
– полная комплексная, активная и реактивная мощности источника питания.
,
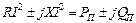где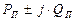 
– активная и реактивная мощности, потребляемые элементами схемы.
Получим уравнение для комплексных мощностей источника и приемника:
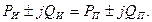
| (38) |
Равенство (38) выражает баланс комплексных мощностей источника и приемника. При равенстве комплексных чисел равны по отдельности их вещественные и мнимые части, следовательно, уравнение (38) можно записать в следующей форме:
 .
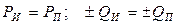| (39) |
Из (39) следует, что для электрической цепи соблюдается закон баланса реактивных мощностей: реактивная мощность, отдаваемая источниками, равна реактивной мощности, потребляемой всеми приемниками.
|
|
|
