 |
Расчет цепей с индуктивно связанными элементами
|
|
|
|
Электрические цепи могут содержать катушки, индуктивно связанные друг с другом. В том случае, когда изменение тока в одной из катушек цепи приводит к появлению ЭДС в другой катушке цепи, говорят, что эти катушки индуктивно связаны, а возникающую ЭДС называют ЭДС взаимной индукции. Степень индуктивной связи катушек характеризуется коэффициентом связи
,
где М – взаимная индуктивность катушек (размерность – Гн); L 1 и L 2 – собственные индуктивности этих катушек.
Следует отметить, что коэффициент связи всегда k < 1.
Пусть имеем две индуктивно связанные катушки с ферромагнитным сердечником (рис. 22). На этом рисунке схематично показана картина магнитного поля при наличии тока i 1 в первой катушке. Витки первой катушки сцеплены с магнитным потоком самоиндукцииФ 11, а витки второй катушки – с магнитным потоком взаимной индукцииФ 21, который отличается от Ф 11 (Ф21< Ф11) за счет наличия потоков рассеяния, сцепленных только с первой катушкой.
 |
Рис. 22
Собственная и взаимная индуктивности равны:
; 
.
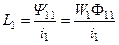Если теперь наоборот пропустить ток i 2 по второй катушке, то соответственно получим:
; 
.
Взаимоиндуктивности катушек равны M 12 = M 21 = M.
Рассмотрим цепь переменного тока (рис. 23), в которую последовательно включены две катушки индуктивности L 1 и L 2, индуктивно связанные друг с другом, и активное сопротивление R.
| При изменении тока i в цепи в катушках индуцируются ЭДС само- и взаимоиндукции. При этом ЭДС взаимной индукции должна по закону Ленца иметь такое направление, чтобы препятствовать изменению потока взаимной индукции. Тогда, если в цепи протекает гармонически | 
|
| Рис. 23 |
изменяющийся ток i = Im sin ωt, то в первой и второй катушках индуцируются ЭДС самоиндукции и взаимной индукции:
|
|
|
;
.
Катушки можно включить так, что ЭДС самоиндукции будет суммироваться с ЭДС взаимоиндукции; при переключении одной из катушек ЭДС взаимоиндукции будет вычитаться из ЭДС самоиндукции. Один из зажимов каждой катушки на схеме помечают, например, точкой или звездочкой. Этот знак означает, что при увеличении, например, тока в первой катушке, протекающего от точки, во второй катушке индуцируется ЭДС взаимоиндукции, действующая от другого конца к точке. Различают согласное и встречное включения катушек. При согласном включении токи в катушках одинаково ориентированы по отношению к их одноименным зажимам. При этом ЭДС само- и взаимоиндукции складываются – случай, показанный на рис. 23. При встречном включении катушек токи ориентированы относительно одноименных зажимов различно. В этом случае ЭДС само- и взаимоиндукции вычитаются. Таким образом, тип включения катушек (согласное или встречное) определяется совместно способом намотки катушек и направлении токов в них.
Перейдем к комплексной форме записи уравнений:
;
,
где 
– сопротивление взаимоиндукции (Ом).
Ток в цепи при согласном включении катушек:
.
Ток в цепи при встречном включении катушек:
.
В качестве примера расчета цепей с индуктивно связанными элементами составим уравнения по методу контурных токов для цепи (рис. 24):
;
.
Рис. 24
Воздушный (линейный) трансформатор. Одним из важнейших элементов электрических цепей является трансформатор, служащий для преобразования величин переменных токов и напряжений и электрического разделения цепей. Передача энергии из одной цепи в другую производится в трансформаторе благодаря явлению взаимоиндукции.
В простейшем случае трансформатор состоит из двух гальванически несвязанных и неподвижных катушек без ферромагнитного сердечника. Такой трансформатор называется воздушным или линейным. Трансформаторы с ферромагнитным сердечником являются нелинейными элементами, т.е. описываются системой нелинейных уравнений и рассматриваются во второй части комплекса.
|
|
|
На рис. 25 представлена схема замещения трансформатора, первичная обмотка которого включена на переменное напряжение U 1, а от вторичной обмотки получает питание приемник с сопротивлением 
.
Рис. 25
В первичной цепи под действием напряжения источника возникает переменный ток, во вторичной цепи за счет магнитной связи катушек индуцируется ЭДС взаимоиндукции, вызывающая протекание тока в нагрузке.
По второму закону Кирхгофа для первичной и вторичной цепей трансформатора можно записать уравнения в комплексной форме:
;
 ,
| (42) |
где 
– напряжение нагрузки.
Решим уравнения (42) относительно 
, предварительно подставив 
и обозначив 
и 
:
,
где 
; 
– вносимые активное и реактивное сопротивления.
Вносимые сопротивления представляют собой такие сопротивления, которые следует включить последовательно с сопротивлениями первичной обмотки, чтобы учесть влияние нагрузки вторичной цепи трансформатора на ток в его первичной цепи.
Контрольные вопросы и задания
1. Каковы основные характеризующие величины синусоидального тока?
2. Сформулируйте определение понятия действующего и среднего значения синусоидального тока.
3. Поясните основы метода изображения синусоидально изменяющихся величин векторами на комплексной плоскости.
4. Мгновенное значение тока 
. Запишите комплекс действующего значения в алгебраической и показательной формах.
5. Как выполнить переход от алгебраической формы записи комплексного тока 
к мгновенному значению?
6. Найдите графически сумму двух периодических синусоидальных токов 
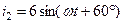. Как определить действующее значение и начальную фазу суммарного тока? Решите эту задачу комплексным методом и постройте векторную диаграмму токов.
7. Дайте определения элементов электрической цепи переменного тока. Запишите уравнения связи мгновенных значений тока и напряжения элементов.
8. Приведите комплексные уравнения и векторные диаграммы идеальных элементов цепи переменного тока (активное сопротивление, индуктивность, емкость).
|
|
|
9. Постройте графики зависимостей индуктивного и емкостного сопротивлений от частоты.
10. Что такое комплексное сопротивление ветви? Закон Ома для цепи синусоидального тока.
11. Что такое комплексная проводимость ветви? Закон Ома при использовании комплексной проводимости.
12. Начертите треугольники сопротивлений и проводимостей и выведите формулы перехода от сопротивлений к проводимостям и обратно.
13. Каково выражение для действующего значения тока в цепи, состоящей из последовательно соединенных элементов R и L (а также R и C), если к зажимам цепи приложено напряжение 
. Постройте векторную диаграмму.
14. Напишите выражение для действующего значения напряжения на зажимах цепи, состоящей из катушки с активным сопротивлением R и индуктивностью L, если мгновенное значение тока 
? Начертите векторную диаграмму.
15. Катушка с параметрами R и L включена параллельно конденсатору емкостью С. Напряжение на зажимах цепи u = 
sin (ω t + 
). Каким будет выражение для действующего значения тока в неразветвленной части цепи?
16. В цепь включены последовательно две катушки с параметрами R 1, XL 1, R 2, XL 2 и конденсатор емкостью С. Каково действующее значение приложенного напряжения U? Напишите выражения для действующего значения тока и коэффициента мощности цепи. Постройте векторную диаграмму.
17. Напишите законы Кирхгофа в комплексной форме.
18. Дайте определения активной, реактивной и полной мощности. В чём заключается их физический смысл? Постройте треугольник мощности.
19. Сформулируйте уравнения баланса комплексных мощностей источника и приемника.
20. Определите условия существования в цепи резонанса напряжений, дайте понятия резонансной частоты, добротности контура, волнового сопротивления, приведите резонансные характеристики.
21. Как определить условия существования в цепи резонанса токов? Дайте понятия волновой проводимостью контура, приведите резонансные характеристики.
22. С помощью каких приборов и по какому признаку можно судить о возникновении резонанса напряжений и токов? Сохранится ли резонанс напряжений, если изменять только напряжение питающей сети?
|
|
|
23. Объясните способ повышения коэффициента мощности электрической цепи при параллельном включении емкости и потребителя с активно-индуктивной нагрузки.
24. Опишите последовательное соединение индуктивно связанных катушек; ток в цепи при согласном и встречном включении катушек.
25. Запишите уравнения воздушного трансформатора, нарисуйте его схему замещения.
Библиографический список
1. Бессонов, Л.А. Теоретические основы электротехники. Электрические цепи: учебник / Л.А. Бессонов; доп. Мин-вом образов. РФ для студ. вузов электротех. спец. – 11-е изд., испр. и доп. – М.: Гардарики, 2007. – 701 с.
2. Демирчан, К.С. Теоретические основы электротехники. В 3 т. Т. 1: учебник / К.С. Демирчан, Л.Р. Нейман, Н.В. Коровкин; доп. Мин-вом образов. РФ для студ. вузов электротех. спец. – 5-е изд. – СПб.: Питер, 2009. – 512 с.
3. Демирчан, К.С. Теоретические основы электротехники. В 3 т. Т. 2: учебник / К.С. Демирчан, Л.Р. Нейман, Н.В. Коровкин; доп. Мин-вом образов. РФ для студ. вузов электротех. спец. – 5-е изд. – СПб.: Питер, 2009. – 512 с.
4. Шебес, М.Р. Задачник по теории линейных электрических цепей: учеб. пособие для электротех. и радиотех. спец. вузов / М.Р. Шебес, М.В. Каблукова – 5-е изд., перераб. и доп. – М.: Высшая школа, 1992. – 544 с.
5. Гуляев, В.В. Расчет линейных электрических цепей: учеб. пособие / В.В. Гуляев, А.А. Кралин, А.С. Репин, И.В. Сычушкин. – Н. Новгород: ФГОУ ВПО «ВГАВТ», 2012. – 44 с.
6. Александров, В.В. Расчет цепей синусоидального тока: учеб. пособие / В.В. Александров, В.В. Гуляев; доп. Мин-вом тр-та РФ для студ. вузов спец. 180404, 180403, 190602. – Н. Новгород: ФГОУ ВПО «ВГАВТ», 2006. – 44 с.
Оглавление
| 1. Основные определения. Изображения синусоидальных функций времени векторами на комплексной плоскости …. | |
| 2. Активное сопротивление, индуктивность и конденсатор в цепи синусоидального тока …………………..……………. | |
| 3. Комплексное сопротивление и проводимость. Законы Ома и Кирхгофа в комплексной форме. Векторные и потенциальные (топографические) диаграммы ……………………… | |
| 4. Мощности – активная, реактивная и полная. Баланс мощностей ………………………………………………………….. | |
| 5. Резонансные режимы в цепи. Резонанс напряжения, резонанс токов. Частотные характеристики резонансных цепей | |
| 6. Расчет цепей с индуктивно связанными элементами ……… | |
| Контрольные вопросы и задания …………………….. | |
| Библиографический список ……………………………………. | |
|
|
|
