 |
Характеристики резонансных цепей
|
|
|
|
Реактивные сопротивления и проводимости отдельных участков цепи могут быть положительными (индуктивные элементы) и отрицательными (емкостные элементы). Поэтому возможны такие сочетания этих элементов, когда входное реактивное сопротивление или входная реактивная проводимость всей цепи равны нулю. При этом ток и напряжение на входе цепи совпадают по фазе и эквивалентное сопротивление всей цепи является активным. Такие режимы цепи называются резонансными.
Резонанс напряжений. На рис. 7 приведена цепь, включающая последовательно соединенные активное сопротивление, индуктивность и емкость. При построении векторных диаграмм этой цепи рассмотрен режим, когда индуктивное и емкостное сопротивления одинаковы по величине (см. рис. 10). Напряжения на индуктивности и емкости полностью компенсируют друг друга. Ток в цепи совпадает по фазе с входным напряжением. В электрической цепи наступает режим резонанса напряжения.
Ток в резонансном режиме достигает максимума, так как полное сопротивление z цепи имеет минимальное значение:
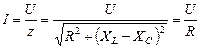 .
.
Условие возникновения резонанса: 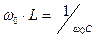 .
.
Частоту  называют резонансной частотой:
называют резонансной частотой:
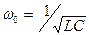 . .
| (40) |
Из (40) следует, что режима резонанса можно добиться следующими способами:
1) изменением частоты;
2) изменением индуктивности;
3) изменением емкости.
В резонансном режиме входное напряжение равно падению напряжения в активном сопротивлении. На индуктивности и емкости схемы могут возникнуть напряжения, значительно превышающие напряжение на входе цепи, если реактивные сопротивления значительно превышают активное сопротивление. Напряжение на индуктивности при резонансе равно напряжению на емкости:
|
|
|
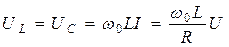 .
.
Отношение 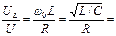 Q называют добротностью контура.
Q называют добротностью контура.
Добротность показывает, во сколько раз напряжения на реактивных элементах превышает входное напряжение в резонансном режиме. В радиотехнических цепях добротность составляет несколько сотен. Резонансные свойства характеризуют также величиной обратной добротности 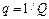 , называемой затуханием контура.
, называемой затуханием контура.
Волновое сопротивление контура или характеристическое сопротивление 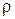 определяет отношение напряжения на реактивных элементах в резонансном режиме к величине тока:
определяет отношение напряжения на реактивных элементах в резонансном режиме к величине тока:
 .
.
При резонансе напряжений малые количества энергии, поступающие от источника и компенсирующие потери энергии в активном сопротивлении, достаточны для поддержания незатухающих колебаний относительно больших количеств энергии магнитного и электрического полей. Покажем, что при резонансе в любой момент времени суммарная энергия магнитного и электрического полей остается постоянной:
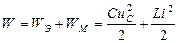 . .
| (41) |
Пусть ток в резонансном контуре 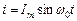 , тогда напряжение на емкости отстает по фазе от тока на 900
, тогда напряжение на емкости отстает по фазе от тока на 900 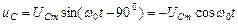 .
.
Суммарная энергия магнитного и электрического полей (41) равна:
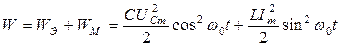 .
.
При резонансе:
 ,
, 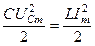 .
.
Следовательно, 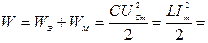 const.
const.
Если в схеме (см. рис. 10) величина ЭДС и параметры R, L, C неизменны, но меняется частота 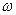 , то изменяется реактивное сопротивление X и, следовательно, полное сопротивление и угол
, то изменяется реактивное сопротивление X и, следовательно, полное сопротивление и угол  . Зависимости параметров двухполюсника (действительной и мнимой части входного сопротивления или входной проводимости) от частоты называют частотными характеристиками.
. Зависимости параметров двухполюсника (действительной и мнимой части входного сопротивления или входной проводимости) от частоты называют частотными характеристиками.
Реактивное сопротивление 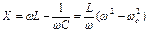 при трех характерных значениях частоты принимает предельные значения, равные нулю, либо бесконечности (рис. 18).
при трех характерных значениях частоты принимает предельные значения, равные нулю, либо бесконечности (рис. 18).
При 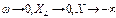 ; при
; при  , при
, при 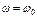 имеет место резонанс напряжений и X = 0. Аргумент функции, при котором она принимает бесконечное значение, называется полюсом функции, а аргумент, при котором она принимает нулевое значение, называется нулевым значением. Отметим, что в момент резонанса происходит изменение характера реактивного сопротивления: при
имеет место резонанс напряжений и X = 0. Аргумент функции, при котором она принимает бесконечное значение, называется полюсом функции, а аргумент, при котором она принимает нулевое значение, называется нулевым значением. Отметим, что в момент резонанса происходит изменение характера реактивного сопротивления: при 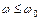 реактивное сопротивление имеет емкостный характер, а при
реактивное сопротивление имеет емкостный характер, а при 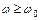 – индуктивный характер.
– индуктивный характер.
|
|
|

Рис. 18
Величина действующего тока в цепи и напряжения на индуктивности и емкости также зависят от изменения частоты:
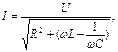
| 
| 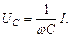
|
Зависимости действующих значений тока и напряжений на элементах цепи при изменении частоты называют резонансными кривыми. Резонансные характеристики 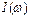 ,
,  ,
, 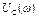 приведены на рис. 19.
приведены на рис. 19.
Напряжение на емкости 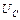 при
при  стремится к U, а при
стремится к U, а при 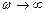 стремится к нулевому значению, напряжение на индуктивности
стремится к нулевому значению, напряжение на индуктивности 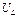 при
при 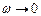 равно нулю, при
равно нулю, при 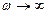 UL стремится к U. При резонансной частоте ω 0 UL = UС и взаимно компенсируются, ток цепи максимален, напряжение источника приложено к активному сопротивлению.
UL стремится к U. При резонансной частоте ω 0 UL = UС и взаимно компенсируются, ток цепи максимален, напряжение источника приложено к активному сопротивлению.

Рис. 19
На рис. 19 видно, что максимум напряжения на индуктивности UL и максимум напряжения на емкости UС имеют место при частотах не равных резонансной частоте. Максимум UL имеет место при частоте, меньшей ω 0, а максимум UС при частоте, большей ω 0.
В электроэнергетических устройствах влияние резонанса, как правило, нежелательное, так как при резонансе напряжения на индуктивных и емкостных элементах могут значительно превышать номинальные значения. Такие явления могут возникать при подключении к зажимам синхронного генератора или трансформатора длинной линии передачи или кабеля, не замкнутых на приемник нагрузки. Генератор и трансформатор имеют индуктивное сопротивление, а линия или кабель обладают емкостью и индуктивностью. При отсутствии нагрузки на конце линии затухание такой цепи очень мало и возникают перенапряжения, если частота близка к резонансной.
Явление резонанса напряжений широко используется в радиопередающих и радиоприемных устройствах.
Резонанс токов. На рис. 11 приведена цепь, включающая параллельно соединенные активное сопротивление, идеальную индуктивность и идеальную емкость. При построении векторных диаграмм этой цепи рассмотрен режим, когда реактивная проводимость цепи b = (bL – bC) = 0 (см. рис. 14). При этом индуктивный и емкостный токи, направленные в противоположные стороны, полностью компенсируют друг друга. Ток в неразветвленной части схемы совпадает по фазе с напряжением. В электрической цепи наступает режим резонанса токов.
|
|
|
Из условия возникновения резонанса тока получим формулу для резонансной частоты тока:
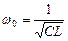 .
.
Полученное выражение для резонансной частоты совпадает с (40). Резонанса токов можно добиться изменением частоты, изменением индуктивности либо емкости.
В режиме резонанса тока полная (входная) проводимость цепи  – минимальна, а полное сопротивление
– минимальна, а полное сопротивление 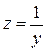 – максимально. Ток в неразветвленной части схемы
– максимально. Ток в неразветвленной части схемы 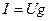 в резонансном режиме имеет минимальное значение, в отличие от резонанса напряжений, когда ток имеет максимальное значение.
в резонансном режиме имеет минимальное значение, в отличие от резонанса напряжений, когда ток имеет максимальное значение.
В идеализированном случае при R = 0 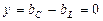 и
и 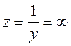 .
.
Ток в неразветвленной части цепи I = 0. Такая схема называется фильтр-пробкой.
При резонансе токов возможны режимы, когда токи через индуктивность и емкость значительно превосходят ток в неразветвленной части схемы. Превышение токов в реактивных элементах над током в неразветвленной части схемы имеет место при условии:
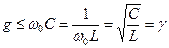 .
.
Величина 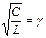 имеет размер проводимости и называется волновой проводимостью контура.
имеет размер проводимости и называется волновой проводимостью контура.
Добротность контура Q при резонансе токов определяет кратность превышения тока в индуктивности 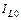 и емкости
и емкости 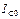 над током в неразветвленной части схемы
над током в неразветвленной части схемы 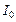 :
:
 .
.
Величина, обратная добротности  ,. является затуханием контура.
,. является затуханием контура.
Энергетические процессы при резонансе токов аналогичны энергетическим процессам при резонансе напряжений. Малые количества энергии, поступающие от источника и компенсирующие потери энергии в активном сопротивлении, достаточны для поддержания незатухающих колебаний относительно больших количеств энергии магнитного и электрического полей. Суммарная энергия магнитного и электрического полей при резонансе токов также в любой момент времени остается постоянной.
Частотные характеристики проводимостей ветвей с индуктивностью  , с емкостью
, с емкостью  и входной проводимости
и входной проводимости 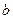 приведены на рис. 20.
приведены на рис. 20.
При ω → 0: bC → 0, bL → ∞, b = (bL – bC) → ∞; при ω → ∞: bL → 0, bC → –∞, b → –∞; при ω = ω 0 имеет место резонанс токов и b = 0. В момент резонанса происходит изменение характера входной проводимости: при ω < ω 0 входная проводимость имеет индуктивный характер, а при ω > ω 0 – емкостной характер.
|
|
|
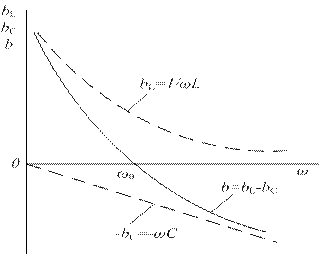
Рис. 20
Резонансные характеристики U(ω), IL(ω), IC(ω) при неизменном входном токе (I = const) и неизменных величинах активного сопротивления, индуктивности и емкости (R = const, L = const, C = const) определяются выражениями 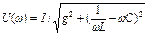 ,
, 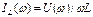 ,
,  и приведены на рис. 21.
и приведены на рис. 21.
При ω = 0 сопротивление индуктивности равно нулю и весь ток протекает через катушку U = 0, I = IL. При  сопротивление конденсатора стремится к нулю и ток проходит только через конденсатор U = 0, I = IL. При частоте резонанса ω = ω 0 I = IL, токи в индуктивности и конденсаторе взаимно компенсируются, входной ток равен току через активное сопротивление I = Ug. Максимумы токов через индуктивность и емкость не совпадают с максимумом напряжения при резонансной частоте ω = ω 0. Максимум IL имеет место при частоте, меньшей ω 0, а максимум IC – при частоте, большей ω 0.
сопротивление конденсатора стремится к нулю и ток проходит только через конденсатор U = 0, I = IL. При частоте резонанса ω = ω 0 I = IL, токи в индуктивности и конденсаторе взаимно компенсируются, входной ток равен току через активное сопротивление I = Ug. Максимумы токов через индуктивность и емкость не совпадают с максимумом напряжения при резонансной частоте ω = ω 0. Максимум IL имеет место при частоте, меньшей ω 0, а максимум IC – при частоте, большей ω 0.
| В энергетике процесс уменьшения угла сдвига фаз между напряжением на приемнике и током, потребляемым из сети, называют компенсацией угла сдвига фаз. Входное сопротивление большинства промышленных предприятий имеет индуктивный характер вследствие массового использования асинхронных двигателей. Для уменьшения вели- |  Рис. 21
Рис. 21
|
чины потребляемого тока за счет компенсации его реактивной составляющей и соответственно потерь электроэнергии в сети, параллельно приемнику энергии включают батареи конденсаторов. Экономически выгодно подключать конденсаторы на возможно более высокое напряжение, так как ток через конденсаторы пропорционален напряжению IC = UωС. Компенсация угла сдвига фаз обычно выполняется до значения коэффициента мощности cos φ = 0,9–0,95.
|
|
|


