Графические методы решения игр

 

Применение алгоритмов линейного программирования для решения стандартных задач далеко не всегда является рациональным. Помимо этого существуют иные методы, которые основываются на использовании специфики данных задач. В настоящем пункте мы остановимся на очень простом классическом способе поиска оптимальных смешанных стратегий в матричных играх, где один из участников имеет только две стратегии (это так называемые 2× п и т ×2 игры).

Для определенности положим, что игрок I имеет возможность выбирать между двумя стратегиями с вероятностями x ₁ и x ₂ = 1 - x ₁, тогда его ожидаемые выигрыши, соответствующие чистым стратегиям игрока II, примут вид

или

т. е. ожидаемые выигрыши могут быть представлены в виде графиков линейных функций, зависящих от переменной x ₁ ∊ [0; 1] На данном рисунке предполагается, что игрок II имеет три стратегии. Линии, изображенные на рисунке задают зависимости среднего выигрыша игрока I от значения вероятности x ₁, с которой он выбирает свою первую стратегию, для случаев, когда его противник выбирает первую, вторую или третью чистую стратегию. Тогда значениям минимального гарантированного дохода первого игрока соответствует нижняя огибающая всех трех прямых. Согласно принципу максимина, оптимальному выбору игрока I будет соответствовать наивысшая точка, лежащая на данной огибающей, отмеченная на рисунке как (x ₁*, z *). Зная ее, можно определить оптимальную смешанную стратегию первого игрока х * = (x ₁*, 1- x ₂*) и цену игры, равную z *.

Исходя из отношения двойственности по оптимальной стратегии первого участника х * однозначно определяется оптимальная стратегия его противника у*. Поскольку у* является результатом решения задачи линейного программирования, то он обладает всеми свойствами допустимого базисного плана, т. е. в случае 2× п игры имеет не более чем две ненулевых компоненты и не менее чем (п -2) нулевых. Номера ненулевых элементов у* определяются номерами линий, пересечение которых определило оптимальную стратегию первого игрока. Действительно, игрок II знает оптимальную стратегию соперника, и применение им стратегий, соответствующих прямым, проходящим выше точки (х ₁*, z *), только увеличило бы его проигрыш.

В рассматриваемом примере это линии z ₂ и z ₃, и, следовательно, в своей оптимальной стратегии второй игрок должен с ненулевыми вероятностями применять вторую и третью чистые стратегии (у ₂ >0, у ₃ >0). Учитывая условие нормировки , можем выразить: y ₃ = l – y ₂ тогда оптимальное значение y ₂* может быть найдено из условия

 или

В результате получаем оптимальную стратегию игрока II у*= (0, у ₂*, у ₃*).

Очевидно, что поиск решения в игре т ×2 осуществляется аналогичным образом с точностью до наоборот: строятся графики ожидаемого проигрыша игрока II, находится их верхняя огибающая и т. д.

Безусловно, графический способ в силу ограниченности круга задач, к которым он может быть применен, имеет скорее теоретическое, чем практическое значение. Однако он хорошо иллюстрирует содержательную сторону процесса поиска решения в игре.

Геометрическое решение игры 2×2

Решению игры 2×2 можно дать хорошо обозримую геометрическую интер­претацию. Пусть имеется игра 2×2 с платежной матрицей

Решение в чистых стратегиях отсутствует. Предположим, иг­рок А выбрал смешанную стратегию (х ₁ х ₂), а игрок В — свою чис­тую стратегию В _i. В этом случае средний выигрыш игрока А опреде­ляется по формуле математического ожидания

, i = 1,2,

поскольку x ₁ + x ₂ = 1. Каждому значению i, согласно v_{B i}, соответ­ствует прямая линия в прямоугольной системе координат. Изобра­зим эти прямые на плоскости.

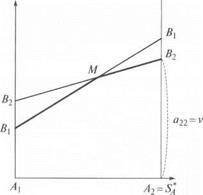
В системе координат на оси абсцисс отложим отрезок А ₁ А ₂единичной длины. Левый конец отрезка (точка с абсциссой х = 0) соответствует стратегии А ₁, а правый конец отрезка (х = 1) — стратегии А ₂. Все промежуточные точки S_A — смешанные стратегии игро­ка А, причем вероятность х ₁стратегии А ₁ находится как расстояние от точки S_A до правого конца отрезка (точки А ₂), а вероятность х ₂ стратегии А ₂ — как расстояние до левого конца (точки А ₁). Через точки А ₁ и А ₂ проведем два перпендикуляра к оси абсцисс: ось I и ось II. На оси I будем откладывать выигрыш при стратегии А ₁ а на оси II — выигрыш при стратегии А ₂.

Пусть противник применяет стратегию B ₁; тогда

v = a ₁₁ + (а ₂₁ – а ₁₁ ) х ₂.

При А ₁, выигрыш равен а ₁₁, а при А ₂ выигрыш равен а ₂₁. Отло­жим эти точки соответственно на осях I и II и обозначим их В ₁, что соответствует одноименной стратегии игрока В. Проведем через эти точки прямую В ₁ В ₁ и будем условно называть ее «стратегией В₁. Очевидно, средний выигрыш игрока А, соответствующий сме­шанной стратегии S_A = (х ₁; х ₂), определяется по формуле матема­тического ожидания  и равен ординате точки М, которая ле­жит на отрезке В ₁ В ₁ и соответствует точке S_A на оси абсцисс, делящей отрезок А ₁ А ₂ в соотношении х ₂ : х ₁.

Аналогичным способом строим стратегию В ₂. Геометрическая иллюстрация игры 2×2 представлена на рис. IV.1.

 

Рис.3.1

 

Необходимо найти оптимальную стратегию S*_A, то есть такую стратегию, при которой, согласно принципу максимина, мини­мальный выигрыш игрока А (при наихудшем для него поведении В) обращался бы в максимум. Поскольку цель игрока В — мини­мизировать выигрыш игрока А за счет выбора своих стратегий, по­строим нижнюю границу выигрыша при стратегиях В ₁, В ₂ (лома­ная В ₁ МВ ₂ отмечена на рисунке жирной линией). На этой границе будет лежать минимальный выигрыш игрока А при любой его сме­шанной стратегии. Поскольку цель игрока А — максимизировать свой выигрыш за счет выбора соотношения х ₂: х ₁, ищем верхнюю точку нижней границы выигрыша. Точка М, в которой этот выиг­рыш достигает своего максимального значения, определяет реше­ние и цену игры. Ордината точки М — цена игры v, ее абсцисса равна , а расстояние до правого конца участка — ,т. е. расстояния от точки 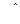 до концов отрезка равны вероятностям  и   стратегий А ₂ и А ₁ в оптимальной смешанной стратегии игрока А.

В рассмотренном примере решение игры определялось точкой пересечения стратегий В ₁, В ₂, но так бывает не всегда; решение определяется именно верхней точкой нижней границы, а эта точка не всегда совпадает с точкой пересечения стратегий.

Рассмотрим два примера. На рис. 3.2 представлен случай, когда оптимальной стратегией игрока А является чистая стратегия А ₂, т. е. . Здесь стратегия А ₂ явно выгоднее стратегии А ₁, независи­мо от поведения противника.

Рис. 3.2

На рис. 3.3 представлен случай, когда заведомо невыгодная стратегия имеется у противника. Для этого случая .

 

Рис. 3.3

Рассмотрим теперь, как определяется оптимальная смешанная стратегия  игрока В. Через верхнюю точку нижней гра­ницы (точка М на рис. 1.1) проведем прямую, параллельную оси аб­сцисс (прямая KL). Доля у ₁ стратегии В ₁ в оптимальной смешанной стратегии 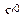  равна отношению длины отрезка K В ₂ к сумме длин отрезков K В ₂ и K В ₁ на оси I:  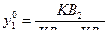  или, что то же самое:    на оси II.

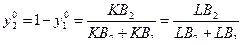
Оптимальную стратегию  можно найти также, если поменять местами игроков А и В, а вместо максимума нижней гра­ницы выигрыша рассматривать, согласно принципу минимакса, минимум верхней границы.

Геометрическое нахождение оптимальных стратегий игрока А, цены игры, нижней и верхней цен игры в чистых стратегиях, седловых точек матрицы игры и доминирующих стратегий игроков можно проводить по следующему алгоритму.

Алгоритм.

1. Берем горизонтальный отрезок [0;1]  (рис. 3.4), на котором для определенности положено a ₂₂ < a ₁₁ < a ₂₁ < a ₁₂.

2.

Рис. 3.4

3. В конце отрезка [0;1] проводим к нему два перпендикуляра: левый, соответствующий стратегии A ₁, и правый, соответствующий стратегии A ₂.

4. На левом перпендикуляре от точки 0 его пересечения с отрезком [0;1] откладываем (как на вертикальной числовой оси) элементы a ₁₁ и a ₁₂ первой строки матрицы А.

5. На правом перпендикуляре от точки 1 его пересечения с отрезком [0;1]  откладываем (как на вертикальной числовой оси) элементы a ₂₁ и a ₂₂  второй строки матрицы А.

Замечания к пунктам 1,3,4: масштабы на левом и правом перпендикулярах должны быть одинаковы, не обязательно совпадающие с масштабом горизонтального отрезка [0;1].

6.  Соединяем точки, изображающие элементы с одинаковыми вторыми индексами, т.е. элементы, стоящие в одном и том же столбце матрицы А: a ₁₁ с a ₂₁   и a ₁₂ с a ₂₂. В результате получаем отрезки: a ₁₁ a ₂₁    и a ₁₂ a ₂₂.

7. Если отрезки: a ₁₁ a ₂₁ и a ₁₂ a ₂₂ неубывающие: a ₁₁ a ₂₁↗ и a ₁₂ a ₂₂↗, то стратегия A ₂  доминирует стратегию A ₁.

Если отрезки a ₁₁ a ₂₁ и a ₁₂ a ₂₂возрастающие, то стратегия A ₂ строго доминирует стратегию A ₁.

8. Если отрезок a ₁₁ a ₂₁ лежит не ниже отрезка a ₁₂ a ₂₂, то стратегия B ₂ доминирует стратегию B ₁. Если отрезок a ₁₁ a ₂₁ лежит выше отрезка a ₁₂ a ₂₂ и не пересекается с ним, то стратегия B ₂  строго доминирует стратегию B ₁.

9. Находим нижнюю огибающую отрезков a ₁₁ a ₂₁ и a ₁₂ a ₂₂.

10. Находим наивысшие точки нижней огибающей.

11. Проектируем их ортогонально на горизонтальный отрезок [0;1].

12. Полученные проекции p ⁰ определяют оптимальные стратегии P ⁰ = (1 - p ⁰, p ⁰)  игрока А.

13. Ордината наивысшей точки огибающей равны цене игры V.

14. Верхний из двух концов нижней огибающей (лежащих на перпендикулярах) есть нижняя цена игры в чистых стратегиях α.

15. Нижний из двух верхних концов отрезков a ₁₁ a ₂₁ и a ₁₂ a ₂₂есть верхняя цена игры в чистых стратегиях β.

16. Если элемент является нижним на перпендикуляре, где он лежит, и верхним концом отрезка a ₁₁ a ₂₁ и a ₁₂ a ₂₂   на котором он лежит, то этот элемент является седловой точкой. В этом случае чистая стратегия игрока В, номер которой совпадает со вторым индексом седловой точки, является оптимальной.

Пункт 15 алгоритма «А» дает возможность достаточно просто геометрически выявить оптимальную чистую стратегию игрока В в случае, если матрица игры содержит седловую точку.

Оптимальные стратегии игрока В геометрически можно находить также и по следующему алгоритму «В».

Решение игры 2× n

Для решения матричных игровых задач, в которых число страте­гий хотя бы одного из игроков равно двум, эффективным является графический способ, аналогичный способу решения задач 2×2.

Рассмотрим сначала игру 2× n. Пусть имеем игру с матрицей

В этой игре игрок А обладает двумя чистыми стратегиями A ₁   и A ₂, а игрок В имеет п чистых стратегий В ₁, В ₂,…, В _n.

Оптимальные стратегии игрока А можно найти по геометрическо­му (графическому) алгоритму «А». Решение задачи находится согласно следующему алгоритму.

1. Определяем нижнюю границу выигрыша.

2. Находим верхнюю точку нижней границы — точку М. Орди­ната этой точки и будет ценой игры v, абсцисса точки М будет равна вероятности x₂ стратегии А ₂ в оптимальной смешанной стратегии игрока А — .

3. Определяем, в результате пересечения каких стратегий была получена верхняя точка нижней границы, — эти стратегии яв­ляются активными, остальные стратегии — пассивные (т. е. их вероятности равны нулю).

4. Далее решаем задачу 2×2 (со стратегиями В ₂ и В ₅) по ранее предложенной схеме, забыв про пассивные стратегии до тех пор, пока не записываем ответ.

Рассмотрим некоторые случаи, которые могут иметь место при определении оптимальной стратегии.

а) Верхняя точка нижней границы выигрыша имеет координаты (0, v)(рис. 3.5а).

 

a

б

в

Рис.3.5

 

В этом случае оптимальной стратегией игрока A является чистая стратегия A ₁, поскольку . Игроку B выгодно применять чистую стратегию, соответствующую прямой, проходящей через точку (0, v) и имеет наибольший отрицательный наклон. Цена игры - v.

б) Верхняя точка нижней границы выигрыша имеет координаты (1, v)(рис. 3.5а).

В этом случае оптимальной стратегией игрока A является чистая стратегия A ₂, поскольку . Игроку B выгодно применять чистую стратегию, соответствующую прямой, проходящей через точку (1, v) и имеет наименьший положительный наклон. Цена игры - v.

в)   Нижняя граница выигрыша имеет горизонтальный участок (рис. 3.5.б).

В этом случае максимум нижней границы будет не в одной точке, а на участке MM ', ордината которого равна v. Решение для игрока A при этом будет неоднозначным: он может применять любую из из своих смешанных стратегий, соответствующих точкам оси абсцисс от N до N '. Таким образом, у игрока A существует несчетное множество оптимальных стратегий

.

Решение для игрока В определяем с помощью граничных точек участка ММ' по тем же правилам, как и в играх 2x2. Так, в точке М'  пересекаются стратегии В ₁ и В ₂. Следовательно, учитывая, что точ­ки L и В ₂ совпадают, т. е. отрезок LВ ₂ равен нулю, имеем:

.

В точке М пересекаются стратегии В ₃ и В ₂. Следовательно, учи­тывая, что отрезок L В ₂ равен нулю, имеем:

.

Таким образом, мы доказали, что стратегия игрока В, которой соответствует горизонтальный участок, является его чистой опти­мальной стратегией.

Алгоритм.

1. Берем горизонтальный отрезок [0,1].

2. Через концы отрезка [0,1] проводим к нему два перпендикуляра: левый и правый.

3. На левом перпендикуляре от точки 0 его пересечения с отрезком [0, 1] откладываем (как на вертикальной числовой оси) все элементы   первой строки матрицы А.

4. На правом перпендикуляре от точки 1 его пересечения с отрез­ком [0, 1] откладываем (как на вертикальной числовой оси) все эле­менты второй строки матрицы А.

Замечания к пунктам 1, 3, 4: масштабы на левом и правом перпен­дикулярах должны быть одинаковы, не обязательно совпадающиес масштабом горизонтального отрезка [0,1].

5. Каждую дару точек, изображающих элементы  и , , стоящие в j-м столбце матрицы А, соединяем отрезком . Таким образом, будут построены п отрезков, представляющих собой графики n линейных функций , ,   j = 1,2,…, n,  где Р = (1 — р, р) — смешанная стратегия игрока А.

6. Если все отрезки 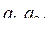,   j = 1,2,…, n,неубывающие (имеют неот­рицательный наклон): 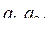↗, , j = 1,2,…, n, то стратегия A ₂ доминирует стратегию A. Если все отрезки 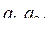, j = 1,2,…, n, возрастающие (имеют поло­жительный наклон):  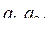то стратегия A ₂ строго доминирует стратегию A ₁.

 

7. Если все отрезки 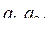, j = 1,2,…, n,   невозрастающие (имеют не­положительный наклон);  (, j = 1,2,…, n, то страте­гия A ₁   доминирует стратегию A ₂.

Если все отрезки 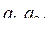, j = 1,2,…, n убывающие (имеют отрица­тельный наклон):  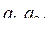↓, (a _{2 j} – a _{1 j} < 0,   j = 1,2,…, n, то стратегия A ₁   строго доминирует стратегию A ₂.

8. Если отрезок  лежит не ниже отрезка , j₁ ≠ j₂;  , то стратегия  доминирует стратегию

Если отрезок  лежит выше отрезка , j₁ ≠ j₂; , то стратегия  строго доминирует стратегию

9. Находим (выделяем) нижнюю огибающую семейства отрезков, которая в общем случае будет представлять собой выпуклую вверх ломаную, а, в частности, может быть и отрезком.

10. На нижней огибающей находим наивысшую точку (точки).

11. Абсцисса р° этой точки является вероятностью выбора игроком А чистой стратегии A₂ в оптимальной смешанной стратегии P ⁰ = (1 - p ⁰, p ⁰).

12.  Ордината наивысшей точки нижней огибающей является це­ной игры V.

13.  Верхний из двух концов нижней огибающей (лежащих на пер­пендикулярах) есть нижняя цена игры в чистых стратегиях a.

14.  Нижний из верхних концов отрезков , j = 1,2,…, n, есть верхняя цена игры в чистых стратегиях β.

15. Элемент матрицы А, изображающая точка которого является нижней на перпендикуляре, где она лежит, и верхним концом отрезка, на котором она лежит, будет седловой точкой игры.

В этом случае чистая стратегия игрока В, номер которой совпадает со вторым индексом седловой точки, является оптимальной.

На рисунке 3.6 из n отрезков , j = 1,2,…, n, указаны три, которые принимают участие в конструировании нижней огибающей, выделенной жирной линией;

N — наивысшая точка этой огибающей; р° — абсцисса точки N, следовательно,

Р° = (1 - р°, р°) — оптимальная смешанная стратегия игрока А; цена игры V равна ординате точки N; нижняя цена игры в чистых стратегия  ; верхняя цена игры в чистых стратегиях 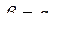; на рисунке видно, что α< V <β.

Рис. 3.6

Решение игры   m × 2

 

Пусть теперь в матричной игре игрок В имеет две стратегии, а иг­рок А - m стратегий. Платежная матрица такой игры выглядит следующим образом:

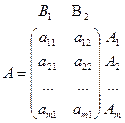
Анализ этой игры во многом напоминает рассуждения, описан­ные для игры . Изобразим m стратегий игрока А в виде m прямых, подобно тому как мы это делали в игре  для игрока В (рис. 3.7).

 

Рис. 3.7

 

Далее находим решение задачи согласно следующему алго­ритму.

1. Определяем верхнюю границу выигрыша.

2. Находим нижнюю точку верхней границы — точку М. Орди­ната этой точки и будет ценой игры v, абсцисса точки М будет равна вероятности  стратегии В ₂в оптимальной смешанной стратегии игрока В - .

3. Определяем, в результате пересечения каких стратегий была получена нижняя точка верхней границы — эти стратегии яв­ляются активными, остальные стратегии — пассивные (т. е. их вероятности равны нулю). На рис. 1.9 активными являются стратегии А ₁ и А ₃ (выделены).

4. Далее решаем задачу 2×2 (с активными стратегиями А ₁ и А ₃)забыв про пассивные стратегии до тех пор, пока не записыва­ем ответ.

В крайних случаях определение оптимальной стратегии игрока А производится аналогично тому, как в игре 2× n определяется опти­мальная стратегия игрока В.

⇐ Предыдущая9101112131415161718Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: