|
Этап 1 – Определение значимости критериев
|
|
|
|
Для этого строится матрица парных сравнений критериев. Пример такой матрицы представлен ниже:

Рис. 3. Матрица парных сравнений 1-ого эксперта
Для оценки значимости используется шкала относительной важности (см. табл.2). Если степень значимости критерия К1 значительно превосходит значимость критерия К3, то в ячейке с адресом G4 ставим 7. Если бы значимость критерия K3 значительно превышала значимость критерия K1, то в клетке G4 была бы поставлена обратная оценка (1/7).
В матрице парных сравнений заполняется только верхний правый треугольник. В нижнем левом треугольнике вводятся расчетные формулы (см. рис. 4)
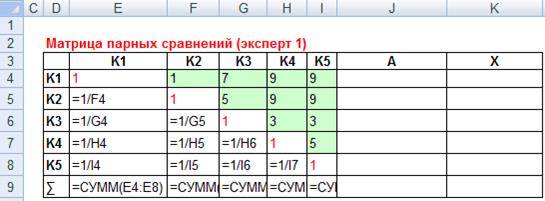
Рис. 4. Формирование матрицы парных сравнений (ввод формул)
Далее необходимо рассчитать собственный вектор матрицы (А) и вектор приоритетов (Х). Компоненты собственного вектора матрицы рассчитываются по формуле средней геометрической, соответственно, в ячейку с адресом J4 необходимо ввести формулу =СРГЕОМ(E4:I4), а затем растянуть ее на весь диапазон ячеек J5:J8.
В итоговой строке данного столбца используется функция =СУММ(J4:J8)
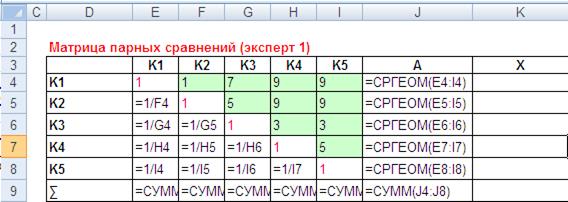
Рис. 5. Расчет собственного вектора матрицы
Далее необходимо определить вектор локальных приоритетов, который и будет показывать значимость сравниваемых критериев с точки зрения данного эксперта. Компонента вектора приоритетов определяется как отношение компоненты собственного вектора матрицы к сумме значений его компонент (см. формулу 5). Соответственно, в ячейку К4 необходимо ввести формулу: =J4/$J$9, а затем растянуть ее на весь блок ячеек.

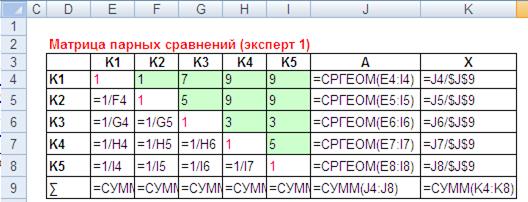
Рис. 6. Расчет вектора приоритетов
Результаты расчетов представлены на рисунке 7.
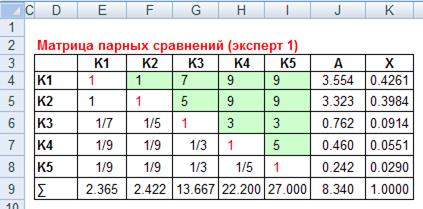
Рис. 7.Значения вектора приоритетов
|
|
|
Далее определяется согласованность проведенных оценок, путем определения отношения согласованности (формула 7). Для упрощения расчетов рекомендуется создать блок вспомогательных ячеек, в который ввести соответствующие расчетные формулы:
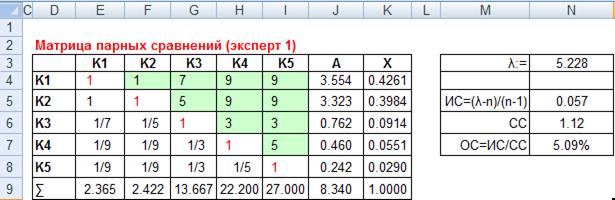
Рис.8. Оценка согласованности мнения эксперта
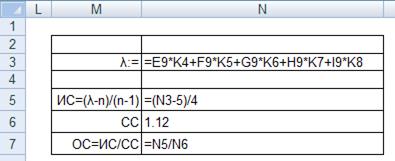
Рис. 9. Формирование блока оценки согласованности мнений экспертов
Поскольку ОС не превышает 20%, то результаты опроса эксперта 1 могут быть использованы в дальнейших расчетах. Аналогичным образом проводится опрос других экспертов и оценивается согласованность их мнений. Затем результаты опросов усредняются и формируется коллективное мнение членов экспертной группы (по формуле средней арифметической простой).

Рис. 10. Определение общего мнения членов экспертной группы
Этап 2 – Определение приоритетов компаний по критерию К1 (гибкость тарифной политики). Для определения приоритетов компаний по критерию «гибкость тарифной политики» необходимо провести их парное сравнение и расставить оценки, заполняя только правый верхний треугольник матрицы.
Перед экспертом ставится вопрос: «Как Вы считаете, у какой компании Х или Y более гибкая тарифная политика? В какой степени (превосходство слабое, значительное, очень сильное)?»
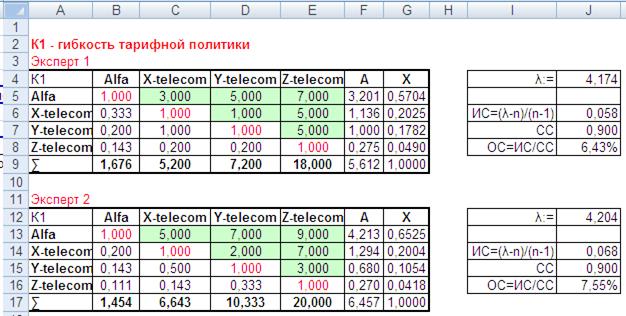
Рис. 11. Расчет локальных приоритетов
Аналогичным образом заполняются матрицы для остальных экспертов и определяетcя обобщенная оценка членов экспертной группы. На 3, 4, 5 и 6 этапах проводятся аналогичные опросы экспертов по остальным критериям. На 7-ом этапе определяется глобальный приоритет рассматриваемых компаний по всем критериям с учетом их значимости.

Рис. 12. Динамические связи

Рис. 13. Расчет глобального приоритета
Для упрощения интерпретации результатов анализа рекомендуется построить лепестковую диаграмму сравнительного анализа и итоговую столбиковую диаграмму компонент вектора глобального приоритета.
|
|
|
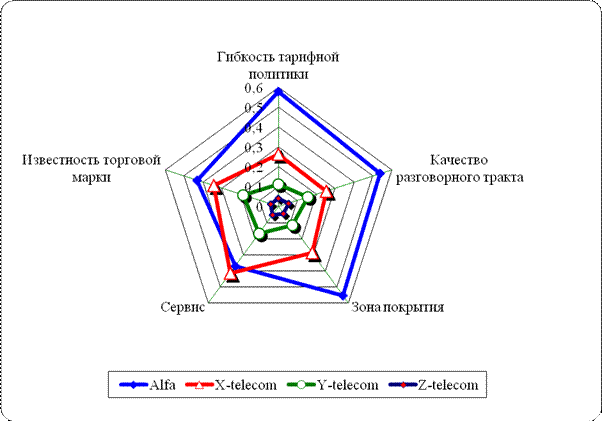
Рис.14. Результаты оценки конкурентных позиций
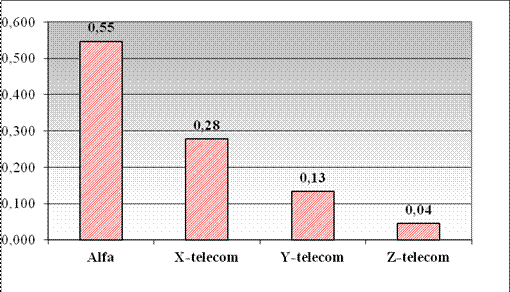
Рис. 15. Значения компонент вектора глобального приоритета
З.1.3. Нечеткие множества
Практика человеческого общения показывает, что не все высказывания сводятся к оценке «истина» или «ложь». Человеку присущи не до конца определенные высказывания, намеки и прочее для описания окружающей ситуации. Например, высказывания «прохладное помещение» или «серое здание» недостаточно четко определены как в смысле температуры, так и цвета. Разные люди эти понятия воспринимают по-разному. Очевидно, что «серый» цвет — это промежуточный оттенок между черным и белым цветами. Если присвоить черному цвету значение 0, а белому — 1, то значение серого цвета будет принадлежать интервалу [0,1]. Именно это обстоятельство побудило Л.А. Заде — известного американского математика — предложить в 1965 г. теорию нечетких множеств, которая получила применение и развитие, как в математике, так и в других науках, в том числе при создании интеллектуальных систем.
Пусть X есть некоторое множество и А — его подмножество, что записывается в форме А 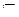 Х. Если элемент х множества X принадлежит подмножеству А, то это отражается в виде х
Х. Если элемент х множества X принадлежит подмножеству А, то это отражается в виде х 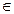 А. Для выражения такой принадлежности можно использовать также характеристическую функцию,
А. Для выражения такой принадлежности можно использовать также характеристическую функцию,  , если х
, если х 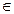 А; иначе
А; иначе 
Рассмотрим теперь множества X и А вида
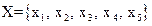 и
и 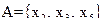 .
.
Запишем для каждого элемента множества X его принадлежность к А:
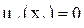 ;
; 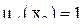 ;
;  ;
;  ;
;  .
.
Тогда множество А можно представить в виде
 .
.
Дополнение к множеству А относительно X будет иметь вид
 ,
,
откуда видно, что
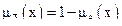
Пусть теперь заданы множества А и В:
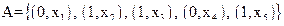
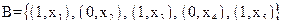 .
.
Тогда при использовании понятий суммы и произведения булевой алгебры, получим:
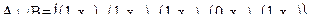 ;
;
 ,
,
т.е. 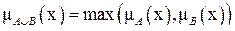 ,
, 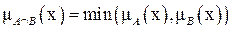 .
.
Пусть X есть универсальное множество и х 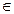 X, а характеристическая функция
X, а характеристическая функция 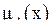 , называемая функцией принадлежности, принимает любое значение из интервала [0,1]. Сам элемент х
, называемая функцией принадлежности, принимает любое значение из интервала [0,1]. Сам элемент х 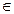 X в разной степени может принадлежать подмножеству А
X в разной степени может принадлежать подмножеству А 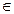 X. Тогда нечетким множеством
X. Тогда нечетким множеством  множества X называется множество упорядоченных пар
множества X называется множество упорядоченных пар 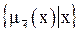 ,
, 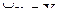 , где
, где  есть степень (или функция) принадлежности х к
есть степень (или функция) принадлежности х к  . Пусть вертикальная линия после
. Пусть вертикальная линия после  будет заменять знак «запятой», если рассматриваются нечеткие множества.
будет заменять знак «запятой», если рассматриваются нечеткие множества.
|
|
|
Сама функция принадлежности — это субъективное представление эксперта об особенностях проводимой операции, характере ограничений и целей исследования. Другими словами, это такой язык математики, который позволяет учитывать нечеткость исходной информации в математических моделях.
Если значение 
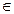 (0;1), то А — есть обычное подмножество множества X. Носителем нечеткого множества
(0;1), то А — есть обычное подмножество множества X. Носителем нечеткого множества 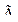 является множество точек
является множество точек 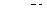 таких, что
таких, что  .
.
Операции над нечеткими множествами
1. Включение
Пусть А, В — нечеткие подмножества множества X. Говорят; что А включено в В (А  В), если
В), если
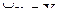 ,
, 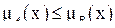 .
.
Пример 3.1.
 .
.
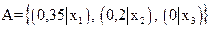 ;
;  .
.

 Или в графической форме (см. рис. 3.1).
Или в графической форме (см. рис. 3.1).
2. Равенство
Говорят, что множество А равно множеству В (А = В), если
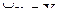 ,
, 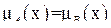 .
.
3. Дополнение
 Множества А и Е дополняют друг друга в двух случаях:
Множества А и Е дополняют друг друга в двух случаях:
если 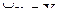
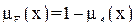 , то
, то 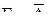 ,
,
если 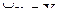
 , то,
, то,  ,
,
Или в графической форме, как показано на рис. 3.2.
4. Пересечение
Пересечение множеств А и В (А 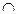 В) — это наибольшее нечеткое множество элементов, одновременно принадлежащих множествам А и В, т.е.
В) — это наибольшее нечеткое множество элементов, одновременно принадлежащих множествам А и В, т.е.
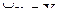
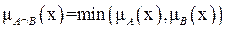
5. Объединение
 Объединение множеств А и В (А
Объединение множеств А и В (А 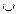 В) — это наименьшее нечеткое множество элементов, содержащее как множество А, так и В (читается «или/и»), т.е.
В) — это наименьшее нечеткое множество элементов, содержащее как множество А, так и В (читается «или/и»), т.е.
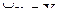
 .
.
Или в графической форме, как показано на рис. 3.3.
Пример 3.2.
 ;
;
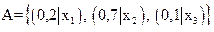 ;
; 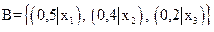 .
.
а)  ;
;
б) 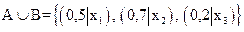 .
.
6. Разность
Разность множеств В и А определяется соотношением
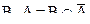
Пример 3.3. Рассмотрим множества, приведенные в примере 3.2. Тогда:
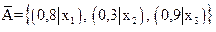 ;
;
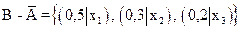 .
.
Однако  (кроме частных случаев:
(кроме частных случаев: 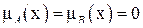 или
или 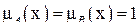 ,
, 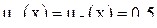 ), что легко проверяется самостоятельно.
), что легко проверяется самостоятельно.
7. Дизъюнктивная сумма («или»)
Дизъюнктивная сумма множеств А и Е определяется соотношением
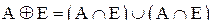 .
.
Следует отметить, что все свойства обычного множества всех подмножеств справедливы и для множества любых нечетких подмножеств, за исключением двух случаев, которые отметим особо.
8. Теоремы Моргана

а) для четких множеств: б) для нечетких множеств:

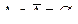

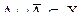
Последние формулы показывают, что в случае нечетких множеств мы уже не имеем дело с алгеброй в смысле обычных множеств.
|
|
|
9. Теорема о декомпозиции.
Всякое нечеткое подмножество 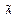 можно разложить на произведение обычных подмножеств по коэффициентам
можно разложить на произведение обычных подмножеств по коэффициентам 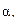 :
:
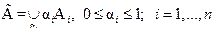 .
.
Здесь операция 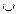 есть объединение множеств.
есть объединение множеств.
Пример 3.4.
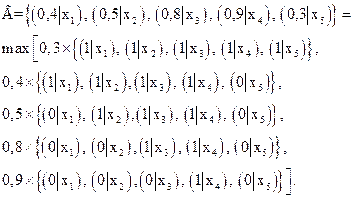 .
.
В состав операций над нечеткими подмножествами включают также операции алгебраических произведений и суммы.
Пусть X — множество и М = [0,1] – связанное с ним множество значений функций принадлежности, а А и В — нечеткие подмножества X.
10. Алгебраическое произведение А*В
Алгебраическое произведение множеств А и В определяется так:
если 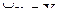 то
то  .
.
Отсюда
 или
или  .
.
11. Концентрирование и растяжение А*В
Операция  называется операцией концентрирования, а операция
называется операцией концентрирования, а операция 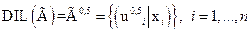 называется операцией растяжения. Применение операции концентрирования к заданному нечеткому множеству моделирует уменьшение нечеткости этого множества в результате поступления некоторой новой информации. В свою очередь, операция растяжения моделирует ситуацию с потерей информации.
называется операцией растяжения. Применение операции концентрирования к заданному нечеткому множеству моделирует уменьшение нечеткости этого множества в результате поступления некоторой новой информации. В свою очередь, операция растяжения моделирует ситуацию с потерей информации.
Эти два оператора используются в представлениях лингвистических неопределенностей в форме CON — «очень» и DIL — «более или менее».
12. Алгебраическая сумма
Алгебраическая сумма нечетких множеств А и В (А 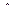 В) определяется следующим выражением:
В) определяется следующим выражением:
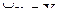 :
: 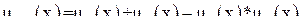
В случае четких множеств
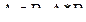 и
и 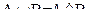
13. Выпуклая комбинация
Выпуклой комбинацией нечетких множеств 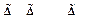 называется нечеткое множество
называется нечеткое множество 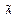 с функцией принадлежности
с функцией принадлежности
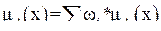 ,
,
где суммирование производится обычным способом по всем 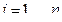 и соблюдается условие
и соблюдается условие  . Эго понятие используется в представлении лингвистических неопределенностей типа «существенно» или «типично».
. Эго понятие используется в представлении лингвистических неопределенностей типа «существенно» или «типично».
Для операций алгебраического суммирования и произведения нечетких множеств свойства 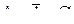 и
и  не выполняются.
не выполняются.
3.1.2. Нечеткие отношения
Рассмотрим два множества X и Y. Пусть х 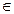 Х, a y
Х, a y 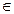 Y. Множество упорядоченных пар (х, у) определяют прямое произведение X
Y. Множество упорядоченных пар (х, у) определяют прямое произведение X 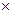 Y. Тогда нечеткое подмножество G, такое что
Y. Тогда нечеткое подмножество G, такое что 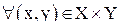 :
: 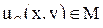 , где М — множество значений принадлежностей элементов множества X
, где М — множество значений принадлежностей элементов множества X 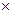 Y (обычно М
Y (обычно М 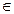 [0,1]) называется нечетким графом.
[0,1]) называется нечетким графом.
Пусть задано некоторое бинарное отношение 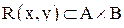 . При этом множество А
. При этом множество А  X можно трактовать как область определения этого отношения, а множество В
X можно трактовать как область определения этого отношения, а множество В  Y — как область значений R(x,y).
Y — как область значений R(x,y).
Пусть Р — прямое произведение п множеств 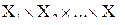 , и М — его множество принадлежностей (обычно М = [0,1]), тоща нечеткое n -арное отношение
, и М — его множество принадлежностей (обычно М = [0,1]), тоща нечеткое n -арное отношение  определяется как нечеткое подмножество Р, т.е.
определяется как нечеткое подмножество Р, т.е.  , принимающее свои значения в М.
, принимающее свои значения в М.
Пример
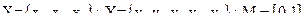
Для двухместного отношения используют табличное представление (или запись вида 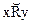 для х
для х 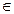 X и у
X и у 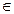 Y):
Y):
|
|
|

| 
| 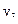
| 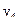
| ||
|
| 0,7 | 0 | 0,1 | 0,3 | 
|
| 0 | 0,6 | 0,4 | 1 | 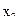
|
В теории нечетких множеств и логики используют символы:
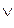 - для обозначения max относительно переменной или элемента x;
- для обозначения max относительно переменной или элемента x;
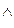 - для обозначения min относительно переменной или элемента x;
- для обозначения min относительно переменной или элемента x;
Объединение двух отношений  и
и  обозначается
обозначается  и определяется выражением
и определяется выражением
 .
.
Пересечение двух отношений  и
и  обозначается
обозначается  и определяется выражением
и определяется выражением
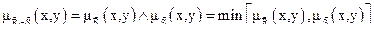 .
.
Для n отношений 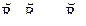
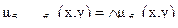 .
.
Рассматривают также:
а) алгебраическое произведение двух отношений:
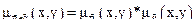 ;
;
б) алгебраическую сумму двух отношений:
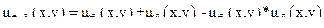 .
.
где знаки «+» и «*» означают соответственно алгебраическое сложение и умножение.
Принцип обобщения
Принцип обобщения для нечетких множеств есть основное равенство, позволяющее расширять область их определения X при отображении или отношении.
Пусть f:X 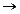 Yесть отображение и
Yесть отображение и  – нечеткое подмножества вида
– нечеткое подмножества вида
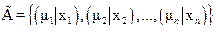 ,
,
тогда
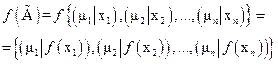
Здесь предполагается, что отображение f взаимно однозначно.
Пример
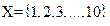 и
и 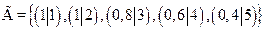 .
.
Тогда, если f есть функция возведения в квадрат, то
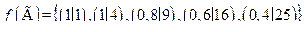 .
.
Необходимо учитывать, что  - это точки множества Y, а
- это точки множества Y, а  - степень принадлежности
- степень принадлежности  нечеткому подмножеству
нечеткому подмножеству 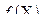 множества Y.
множества Y.
Принцип обобщения позволяет расширить область определения X отображения f, включив в нее наряду с точками также произвольные нечеткие подмножества множества X.
Композиция двух нечетких отношений
Пусть  и
и 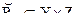 . Тогда «max-min» - композиция отношений
. Тогда «max-min» - композиция отношений 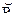 и
и 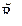 (обозначается
(обозначается  ) определяется выражением:
) определяется выражением:
 где
где 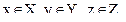
Пример

| 
| 
| 
| ||
|
| 0,3 | 0,5 | 0 | 0,2 | 
|
| 0,8 | 0 | 1 | 0,4 | 
|
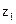
| 
| 
| ||
|
| 0,3 | 0,9 | 0,4 | 
|
| 0,8 | 0,2 | 0 | 
| |
| 0,1 | 0,8 | 1 | 
| |
| 0,5 | 0,4 | 0 | 
|
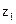
| 
| 
| ||
|
| 0,5 | 0,3 | 0,3 | 
|
| 0,4 | 0,8 | 1 | 
|
Пример определения элемента  отношения
отношения 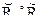 :
:
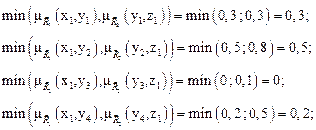
тогда 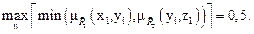
Для элемента 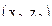 будем иметь:
будем иметь:
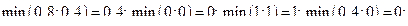

Так же вычисляются остальные элементы отношения 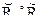 .
.
Операция «max-min» композиции ассоциативна, т.е.
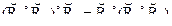
Теорема декомпозиции
Любое нечеткое отношение 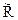 можно представить в виде
можно представить в виде
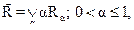
где
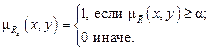
Здесь запись  обозначает, что все элементы обычного четкого отношения
обозначает, что все элементы обычного четкого отношения 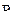 умножаются на
умножаются на  . При этом если
. При этом если 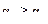 , то
, то  .
.
Нечеткие системы
ХХ век ознаменовался быстрым ростом объемов новых вычислительных технологий, которые позволили улучшить наши способности к познанию окружающего мира. Среди группы таких технологий следует выделить те, которые связаны с интеллектуальными методами решения различных задач в промышленности, экономике, медицине, строительстве и других областях деятельности на основе их обучения на доступных имеющихся данных.
В настоящее время значительно возрастает применение новых интеллектуальных технологий (нечетких систем, нейронных сетей, эволюционных алгоритмов и др.) в разных областях деятельности.
Ранее было показано, что нечеткий вывод осуществляется по правилу композиции двух нечетких отношений, первое из которых (слева направо) определяет нечеткое множество исходных параметров, например,  , второе же отношение устанавливает взаимосвязь этого множества с нечетким множеством
, второе же отношение устанавливает взаимосвязь этого множества с нечетким множеством
 выходных параметров и интерпретируется высказыванием «если
выходных параметров и интерпретируется высказыванием «если  , то
, то  ». Такую операцию называют композиционным правилом вывода. Если имеем набор подобных высказываний о разных ситуациях, то этот набор можем назвать нечеткой базой знаний, или нечеткой базой правил.
». Такую операцию называют композиционным правилом вывода. Если имеем набор подобных высказываний о разных ситуациях, то этот набор можем назвать нечеткой базой знаний, или нечеткой базой правил.
Нечеткие высказывания в базе правил удобно представлять так, чтобы внутри каждого из этих высказываний нечеткие переменные связывались логической операцией «и», а сами правила объединялись между собой операцией «или». Тогда некоторое k-е нечеткое правило или высказывание в базе правил можно представить в следующем виде:
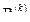 : «Если x1 это
: «Если x1 это 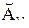 и x2 это
и x2 это 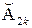 и... и x n это
и... и x n это 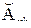 ,
,
то y1 это 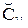 и y2 это
и y2 это 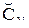 и... и y m это
и... и y m это 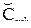 »,
»,
где  , (
, (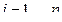 ) и
) и 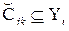 , (
, ( ) являются термами соответственно входных и выходных лингвистических переменных.
) являются термами соответственно входных и выходных лингвистических переменных.
Если y1, y2,…, y m взаимно независимы, то k-е нечеткое правило можно
представить следующим образом:
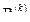 : «Если x1 это
: «Если x1 это 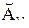 и... и x n это
и... и x n это 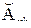 , то y это
, то y это  »,
»,
где 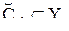 ,
,  и
и  ; m — число выходных переменных, а
; m — число выходных переменных, а
N — общее число правил.
Нечеткий логический вывод
Определение. Нечетким логическим выводом называется заключение в форме нечеткого множества, полученного на основе текущих значений входов с использованием нечеткой базы правил и нечетких операций.
Для проведения нечеткого логического вывода должны выполняться следующие условия.
1. Существование хотя бы одного правила для каждого лингвистического терма выходной переменной.
2. Для любого терма входной переменной имеется хотя бы одно правило, в котором этот терм используется в качестве предпосылки (левая часть правила).
3. Отсутствует противоречивость и корреляция между правилами.
Введем следующие обозначения:
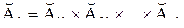 и
и 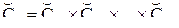 .
.
Тогда правила можно представить в виде:
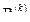 :
: 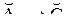 , k= 1, 2,…, N.
, k= 1, 2,…, N.
Такое выражение отражает нечеткое причинное отношение предпосылки и заключения. С другой стороны, 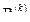 можно интерпретировать как нечеткое отношение, определенное на множестве X
можно интерпретировать как нечеткое отношение, определенное на множестве X 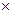 Y; т.е.
Y; т.е. 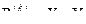 , с функцией принадлежности
, с функцией принадлежности
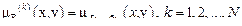
Тогда возможно применение к базе правил композиционного правила нечеткого логического вывода.
Рассматриваемые высказывания (правила) связаны между собой в базе правил связкой «или», которая соответствует операции объединения нечетких множеств. Осуществляя эти действия, на заданном множестве Y получим геометрическую фигуру, которая будет являться функцией принадлежности нечеткого множества, полученного в результате нечеткого логического вывода.
В блоке «нечеткий логический вывод» сначала на графических представлениях элементов левой части каждого правила определяют уровни их отсечения по величине  и находят среди них минимальное значение
и находят среди них минимальное значение
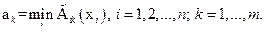
Затем по величине для правой части каждого k -го правила проводят отсечение верхней части соответствующих функций принадлежности. В результате получим в каждом правиле усеченную функцию принадлежности 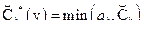 . Далее осуществляется объединение полученных усеченных функций принадлежности
. Далее осуществляется объединение полученных усеченных функций принадлежности 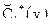 на множестве Y с использованием операции max. В итоге получаем результирующую функцию принадлежности нечеткого логического вывода
на множестве Y с использованием операции max. В итоге получаем результирующую функцию принадлежности нечеткого логического вывода
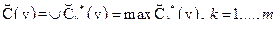 .
.
Для перехода от результата нечеткого вывода к «усредненному» четкому выводу применяют метод дефазификации. Существуют несколько таких методов, например, метод среднего центра, метод суммы центров, метод максимума итоговой функции принадлежности, метод центра тяжести (центро- идный метод) и др. Центроидный метод заключается в нахождении центра тяжести фигуры, образованной функцией принадлежности 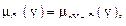 по формуле
по формуле
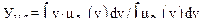 ,
,
где интегрирование производится по области определения функции принадлежности нечеткого множества  .
.
Эта координата и будет «усредненным» четким результатом нечеткого вывода для рассматриваемой ситуации.
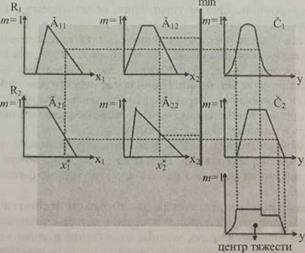
Нечеткий логический вывод по Э. Мамдани, является наиболее распространенным способом его реализации и опирается на нечеткую базу правил. Поэтому, далее на рис. 3.4 показана графическая интерпретация нечеткого логического вывода по Э. Мамдани.
|
|
Рис. 3.4. Изображение нечеткого логического вывода по Э. Мамдани
Системы с нечеткой логикой целесообразно применять тогда, когда для сложных процессов отсутствуют простые математические модели или экспертные знания можно сформулировать только в словесной форме. Далее также приведен конкретный пример использования нечеткого логического вывода в сфере строительной деятельности.
В заключение приведенного изложения по нечеткой логике приведем слова Л. Заде: «Основной принцип нечеткой логики — это использовать неточность и неполную достоверность для достижения удобства, робастности, низкой цены решения и хорошего соответствия реальности».
Следует также отметить, что аппарат нечетких множеств и нечеткой логики с успехом применяется для решения слабо формализованных задач или задач с ненадежными исходными данными. Этому обстоятельству способствует, во-первых, доказательство американским ученым Б. Коско в 1992 г. теоремы о том, что «любая математическая система может быть аппроксимирована системой, основанной на нечеткой логике». Во-вторых, хотя набор нечетких правил в базе знаний, используемые вид и параметры функций принадлежности могут не вполне отражать реальную действительность, эти недостатки можно откорректировать с использованием нечетких адаптивных систем, например, нечетких нейронных сетей.
3.1.3. Применение аппарата нечетких множеств
Нечеткое управление движением
подъемного крана на объекте строительства
Применение нечетких систем обеспечивает принципиально новый подход к проектированию систем управления, используемых в строительных организациях.
В процессе возведения строительного объекта, при перемещении грузов с помощью крана часто возникают его колебания, амплитуды которых зависят от веса и формы груза, направления и способа подъема, длины груза и развиваемых при этом ускорений. Применение регуляторов допустимо тогда, когда имеется возможность перестраивать их параметры непрерывно в процессе функционирования. Но активные алгоритмы управления долго отлаживаются, да и достаточно дорогие сами по себе.
Точная математическая модель реального строительного объекта часто оказывается чрезмерно сложной. Да и изменения окружающей среды также приводят к действиям на объект различных возмущений: физических, структурных и др.
Применение нечеткого регулятора для этих целей требует лишь использования необходимого числа локальных правил, которые связывали бы требуемую скорость движения крана, угловое отклонение и угловую скорость колебания груза. Это реализуется на основе способности нечеткого регулятора «экстраполировать» свое поведение с учетом изменения окружающей среды (ветер, снег и т.п.) и своевременно проводить корректировку своих действий. При этом затраты на проектирование оказываются значительно меньше, чем в традиционных методах, а точность регулирования сохраняется.
Применение нечеткой логики обеспечивает принципиально новый подход к проектированию систем управления, в которых раньше данные, цели и ограничения являлись чрезмерно сложными или плохо определенными.
Такие проблемы можно решить, если использовать подход Э. Мамдани с помощью реализации (построения) классической структурной схемы нечеткого управления. Эта схема основана на эмпирически приобретенных знаниях о функционировании объекта (процесса) и представленной в лингвистической форме некоторой совокупности правил.
Так, например, нечеткий регулятор фирмы OMRON — Electronic имеет всего три входные переменные для управления, например, строительным краном: V желаемое — задающее воздействие («уставка») для скорости движения крана;
Q — угол отклонения груза;
dQ/dt — угловая скорость колеблющего груза.
Управляющее воздействие на выходе нечеткого регулирования осуществляет сигнал скорости V, подаваемый на привод крана
Нечеткий регулятор реализует следующие функции:
• ввод (с помощью аналого-цифровых преобразователей) значений угла Q отклонений груза и команд управления от крановщика на изменение скорости и направление движения крана V желаемое;
• фазификация указанных значений с использованием лингвистически
|
|
|