Арбитражная схема Нэша. Равновесие Нэша

Более общим критерием оптимального решения игры является равновесие Нэша (Nash equilibrium), названное в честь Дж. Нэша, кото­рый предложил этот критерий. Равновесие Нэша предполагает такую ситуацию в игре (такой профиль стратегий), при которой ни одному из игроков невыгодно сепаратно (в одностороннем порядке, когда другие участники не меняют решения) отходить от выбранной страте­гии. Это ситуация, в которой ни один из игроков не может увеличить свой платеж за счет только собственных действий. Равновесие Нэша и его модификации признаются наиболее подходящими концепциями решения бескоалиционных игр.

Равновесие Нэша — это профиль стратегий (один и тот же для всех игроков), при котором стратегия каждого игрока обеспечивает ему наи­лучший отклик (best response) на стратегии других игроков, т.е. обеспе­чивает максимальный платеж при стратегиях всех остальных игроков. Таким образом, при равновесии по Нэшу ни у одного из игроков нет стимула в одностороннем порядке изменять свою стратегию. Эта кон­цепция основана на предположении максимизации выигрыша, к ко­торой стремится каждый игрок, и на рациональном ожидании (пред­ставлении) каждого игрока относительно поведения других игроков.

Логические основания этой концепции решения игры можно объ­яснить следующим образом. В силу гипотезы рационального поведе­ния каждый игрок стремится выбрать наилучшие для него действия при заданной обстановке, а обстановку эту определяют в том числе и другие игроки, рассуждающие подобным образом. Очевидно, что для реализации такого равновесия требуется не только инфор­мированность каждого игрока о допустимых стратегиях и платежных функциях всех игроков, но и информированность всех игроков о вза­имной информированности. То есть для того, чтобы предположения о рациональном поведении оправдывались, необходимо выполнение принципа общего знания.

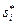Принцип рационального нахождения решения игры означает, что каждый игрок i формирует предположение о действиях остальных игроков  и выбирает в качестве своей стратегии  наилучший ответ на эти предполагаемые действия. Принцип рациональности и общего знания делает возможным (по крайней мере гипотетически) совпаде­ние  с действительным выбором другими игроками своих страте­гий. Таким образом, игрок i выбирает 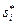 потому, что это наилучший отклик на стратегии  других игроков, которые являются наилучшим откликом на стратегию .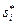

Математически равновесие Нэша можно определить следующим образом. Ситуация s ^* в игре называется равновесием Нэша, если для любого игрока i и любой его стратегии  выполняется нера­венство , т.е. . Стратегия   яв­ляется наилучшим откликом на  для игрока i  в такой ситуации у игроков нет причин сепаратно отклоняться от своих оптимальных стратегий.

Дж. фон Нейман и О. Моргенштерн предложили потребовать от множества дележей, которое принимается в качестве решения кооперативной игры следующие два свойства: внутреннюю устойчивость, состоящую в том, чтобы дележи из решений нельзя было противопоставить друг другу, и внешнюю устойчивость, состоящую в возможности каждому отклонению от решения противопоставлять некоторый делёж, принадлежащий решению. В результате мы приходим к следующему определению.

Решением по Нейману-Моргенштерну (Н-М-решением)кооперативной игры называется множество R дележей в нём, обладающее следующими свойствами:

1) внутренняя устойчивость: никакие два дележа из R не доминируют друг друга;

2) внешняя устойчивость: каков бы ни был делёж S, не принадлежащий R, найдётся делёж r, принадлежащий R, который доминировал бы S.

Содержательная интерпретация Н-М-решения состоит в том, что любые две нормы поведения, соответствующие Н-М-решению, не могут быть противопоставлены друг другу; каково бы ни было отклонение от допустимых поведений, найдётся такая коалиция, которая будет стремиться к восстановлению нормы.