Применение теории игр в процедурах принятия решений

 Одной из наук, предоставляющей возможность математического описания постановок различных задач по принятию решений и математическое обоснование подходов к их анализу, является теория игр, представляющая собой теоретические основы математических моде­лей принятия оптимальных решений в конфликтных рыночных отно­шениях, носящих характер конкурентной борьбы.

Теория игр представляет собой теоретические основы построения и анализа на основе математического и компьютерного моделирования для принятия оптимальных решений в конфликтных рыночных отношениях, носящих характер конкурентной борьбы. Использование теории игр позволяет более обоснованно принять решение и провести критический анализ ситуации с учетом реальных факторов. Теория игр представляет собой комплекс математических моделей и логико-математический аппарат для анализа и разработки стратегий и принятия оптимальных решений в условиях конфликта интересов и неопределенности поведения. На сегодняшний день теория игр предлагает пути и методы решения сложных стратегических задач в самых различных областях.

Антагонистические игры

 

Рассмотрим  антагонистические игры и их основные свойства. А нтагонистической игрой называется игра с ненулевой суммой, в которой участвуют два игрока. Выигрыш одного игрока осуществляется за счет проигрыша другого, т.е. их платежи прямо противоположны. Формально антагонистическая игра мо­жет быть представлена как   G (X, У, U), где X и Y — множества стра­тегий игроков 1 и 2 соответственно; U — платежная функция игро­ка 1, ставящая в соответствие каждой ситуации (т.е. паре стратегий (х, у)) действительное число, соответствующее полезности игрока 1 при реализации данной ситуации. Так как интересы игроков прямо противоположны, функция U одновременно представляет и прои­грыш игрока 2.

Если у игроков конечное число чистых стратегий, то такие анта­гонистические игры называют матричными, так как платежи игроков обычно представляются платежной матрицей игрока 1. Этого доста­точно для описания игры, поскольку платежная матрица игрока 2 со­стоит из тех же элементов, но со знаком «—».

Антагонистические игры являются сравнительно простыми и до­вольно приближенными моделями реальных ситуаций, характеризу­ющихся взаимосвязанностью действий участников и противополож­ностью интересов, но их применение связано с рядом существенных ограничений.

Во-первых, антагонистические игры не могут моделировать кон­фликты с числом участников больше чем два (по определению). Вме­сте с тем такие многосторонние конфликты не только встречаются в действительности, но являются принципиально более сложными, чем конфликты с двумя участниками.

Во-вторых, «чистый» антагонизм интересов присутствует в игровых отношениях нечасто (например, в боевых действиях, спортивных со­стязаниях). Даже в конфликтах с двумя участниками интересы сторон необязательно противоположны; часто случается так, что одна из си­туаций оказывается предпочтительнее другой для обоих участников.

В-третьих, антагонистические игры не рассматривают возможность соглашений, компромиссов и коопераций.

Тем не менее, несмотря на значительные ограничения, матрич­ные игры могут использоваться для моделирования многих конфлик­тов, поэтому считаем полезным рассмотреть эту игровую модель, так как на ее примере можно хорошо проиллюстрировать основы исполь­зования математического аппарата теории игр. Кроме того, теория антагонистических игр очень хорошо развита, существуют различные методы поиска их решения, классические антагонистические игры до­вольно просты, и к ним могут быть сведены некоторые более сложные игры. В антагонистических играх принципиальные основы поведения игроков отчетливо ясны. Поэтому анализ более общих игр становит­ся проще и понятнее, если уже освоены принципы анализа и решения антагонистических игр.

Исторически антагонистические игры являются первым классом математических моделей теории игр, и этот класс игр имел большое значение для становления современной теории игр. В настоящее вре­мя антагонистические игры рассматриваются как часть более широко­го класса некооперативных игр. Антагонистические игры до сих пор изучаются и применяются специалистами, на их основе разрабатыва­ются новые методы изучения и понимания конфликтов.

Матричная игра может рассматриваться как следующая абстракт­ная игра двух игроков. Игрок 1 имеет т чистых стратегий i = 1,2, …, m; игрок 2 имеет п чистых стратегий j = 1,2,..., п. Число чистых стратегий игроков определяет множество ситуаций в игре (всего таких ситуа­ций m×n. Для каждой ситуации должен быть определен платеж. Так как игра антагонистическая, достаточно определить платеж одного из игроков. Пусть каждой паре стратегий (i, j)поставлено в соответ­ствие число а_ij, выражающее выигрыш игрока 1 за счет игрока 2, если игрок 1 выберет свою i -ю стратегию, а 2 — свою j-ю стратегию.

Платежи игроков связаны соотношением , так как выи­грыш игрока 1 равен проигрышу игрока 2 при избрании ими любых стратегий. Следовательно, в платежной матрице такой игры в каждой паре числа равны по модулю и противоположны по знаку. Чтобы упро­стить записи, для представления матричной игры используются толь­ко платежи игрока 1 а_ij;а платеж игрока 2: b_ij = - а_ij.

Игрок I выбирает свою i-ю стратегию , 2 — свою j-ю стратегию 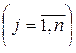, после чего игрок 1 получает выигрыш а_ij за счет игрока (если а_ij <0, это значит, что игрок 1 передает игроку 2 сумму \ а_ij\). На этом игра заканчивается. Платежи игрока 1 представляются в виде матрицы, строки которой соответствуют стратегиям игрока 1, а столб­цы — стратегиям игрока 2.

Таким образом, матричная игра полностью задается платежной матрицей игрока 1 (для игрока 2 матрица выигрышей будет — А):

.

Такой же моделью может быть представлена и игра с постоянной суммой a_ij + b_ij = const, так как любая игра с постоянной суммой может быть приведена к игре с нулевой суммой.

При анализе антагонистических игр, как и при анализе любой игры, предполагается, что каждый игрок действует наилучшим для себя обра­зом, т.е. пытается получить максимально возможный платеж при лю­бых стратегиях противника, считая, что противник также действует наилучшим для себя образом.

Решение матричных игр базируется на пессимистическом крите­рии оптимальности, основанном на том, что игроки будут стремить­ся максимально уменьшить платежи друг друга (тем самым увеличить собственные платежи), т.е. стремиться «сделать друг другу как можно хуже». Этот критерий оптимальности реализуется в поиске равновесия в осторожных (prudent) стратегиях. Согласно такому подходу, стратегия игрока является оптимальной, если применение этой стратегии обе­спечивает ему наилучший гарантированный результат (security level) при всевозможных стратегиях другого игрока. Следовательно, игрок 1 считает, что при выборе им любой стратегии (любой строки платежной матрицы) противник выберет столбец, дающий ему максимальный выигрыш, т.е. минимальный для игрока 1. Тогда оптимальная страте­гия игрока 1 — выбрать самый большой из минимальных платежей.

Исходя из этих позиций, игрок 1 для каждого значения i (i = 1,m) должен определить минимальное значение платежа в зависимости от применяемых стратегий игрока 2: 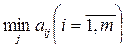, т.е. определяется минимальный выигрыш для игрока 1 при условии, что он примет свою i -ю чистую стратегию, затем из этих минимальных платежей отыски­вается такая стратегия i = i ⁰, при которой этот минимальный платеж будет максимальным, т.е. находится .

Эта стратегия гарантирует наибольший (неуменьшаемый) платеж независимо от стратегии противника. Такая стратегия также называет­ся максиминной стратегией (стратегия максимизации минимального выигрыша).

Число v ₁  называется нижней чистой ценой игры (или максимином) и показывает, какой выигрыш может гарантировать себе игрок 1 при всевозможных действиях игрока 2.

Аналогично рациональный игрок 2 должен стремиться за счет своих стратегий максимально уменьшить выигрыш игрока 1. Поэтому для игрока 2 отыскивается , т.е. определяется максимальный платеж игрока 1, при условии, что игрок 2 применит свою j -ю чистую стра­тегию, затем игрок 2 отыскивает такую стратегию j = j⁰,при которой игрок 1 получит минимальный платеж, т.е. находит .

Эта стратегия гарантирует игроку 2 наименьший (неувеличиваемый) проигрыш. Такая стратегия называется минимаксной стратегией (стратегия минимизации максимального проигрыша).

Число v₂называется чистой верхней ценой игры (или минимаксом) и показывает, какой максимальный выигрыш игрок 2 может позволить получить игроку 1.

Другими словами, применяя свои чистые стратегии, игрок 1 может обеспечить себе выигрыш не меньше v₁ а игрок 2 за счет применения своих чистых стратегий может не допустить выигрыш игрока 1 больше, чем v₂.

Если в игре с матрицей A v₁ = v₂,то говорят, что эта игра имеет седловую точку и чистую цену игры.

v = v₁ = v₂.

Седловая точка — это пара чистых стратегий (i⁰, j⁰) соответствен­но игроков 1 и 2, при которых достигается равенство v₁ = v₂. В это понятие вложен следующий смысл: если один из игроков придер­живается стратегии, соответствующей седловой точке, то другой игрок не сможет поступить лучше, чем придерживаться стратегии, также соответствующей седловой точке. Математически это можно записать как

, где i, j — любые чистые стратегии соответственно игроков 1 и 2; (i⁰, j⁰) - стратегии, образующие седловую точку.

Таким образом, седловой элемент  является минимальным в i ⁰-й строке и максимальным j ⁰-м столбце в матрице А. Отыскание седло­вой точки матрицы А происходит следующим образом: в матрице А по­следовательно в каждой строке находят минимальный элемент. Если этот элемент является максимальным в своем столбце, то он и есть седловой элемент, а пара стратегий, ему соответствующая, образует седловую точку. Пара чистых стратегий игроков 1 и 2, образую­щая седловую точку и седловой элемент , называется решением игры. При этом i ⁰ и j ⁰ называются оптимальными чистыми стратегиями соответственно игроков 1 и 2.

Решение матричной игры может быть не единственным. Возмож­ны ситуации, когда в игре есть несколько седловых точек, но все они обеспечивают одну цену игры. Например, в игре с матрицей

Существует две ситуации равновесия (1, 1)и(1, 3).

Поиск решения матричной игры начинается с поиска доминиру­ющих стратегий и нахождения седловой точки. Если матричная игра имеет седловую точку в чистых стратегиях, то ее нахождением закан­чивается решение игры. Если же в игре нет седловой точки, то мож­но найти нижнюю и верхнюю чистые цены игры, которые указывают, что игрок 1 не должен надеяться на выигрыш больший, чем верхняя цена игры, и может быть уверен в получении выигрыша не меньше нижней цены игры.

Платеж меньше v₁ игрок 1 получит, если будет вести себя «нера­ционально» (глупо или азартно). Если у него есть какая-то дополни­тельная информация о решениях игрока 2, он может увеличить свой платеж до v₂.Однако игрок 2, действуя «рационально», не позволит игроку 1 получить больше v₂. Больший платеж может быть получен в случае «нерациональных» действий игрока 2 (намеренная помощь рассматривается как «нерациональное» поведение).

В примере конкуренции предприятий игрок 1 считает, что независимо от его стратегии выбора про­дукции для производства (т.е. независимо от выбора им строки пла­тежной матрицы) игрок 2 выберет стратегию (столбец платежной ма­трицы), максимизирующую его платеж, т.е. минимизирующую платеж игрока 1. Поэтому игроку 1 нужно найти минимальный платеж в каж­дой строке платежной матрицы и рассматривать только его. Этот пла­теж ему гарантирован. Игрок 2 также рассматривает наихудшие варианты и стремится обе­спечить себе максимальный выигрыш (минимальный выигрыш своему противнику).

Исход игры, имеющей седловую точку, объективно обусловлен и предопределен. В случае «рациональности» игроков результат игры не зависит от искусности или опыта игроков, а зависит лишь от усло­вий игры (платежной матрицы). Поэтому такие игры называют вполне (полностью) определенными. Седловая точка соответствует равновесию в игре. Если один из игроков выбирает стратегию, соответствующую положению равновесия, то другому также выгоднее всего избрать стратегию, отвечающую седловой точке. Тогда каждый игрок получает свой гарантированный платеж (выигрыш или проигрыш). Выбор дру­гой стратегии уменьшает прибыль или увеличивает потери.

Выбор каждого из игроков своей оптимальной стратегии нет смыс­ла скрывать от противника, так как он не сможет ухудшить результат. Это свойство может быть использовано, например, для определения исходных позиций сторон при переговорах.

Равновесие в матричных играх минимизирует риск, поскольку основано на принципе: каждый игрок должен выбирать не ту стра­тегию, которая приносит ему наибольший выигрыш при неразумном выборе стратегии соперником, а ту стратегию, которая в наибольшей степени предохраняет от потерь в игре с «разумным» соперником.

 

Теорема. Пусть V - цена игры, 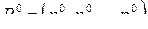 и   – оптимальные смешанные стратегии соответственно игроков А и В. Тогда справедливы следующие утверждения.

1. Для любой смеси активных стратегий  игрока А справедливо равенство H (P, Q ⁰) = V.

2. Для любой смеси активных стратегий  игрока В справедливо равенство H (P ⁰, Q) = V.

Пусть имеем [ т х п ] - игру с матрицей выигрышей А игрока А

.

Ситуация (А _k,B _l), сложившаяся в результате выбора игроками А и В соответственно стратегий А _k и B _l , , называ­ется удовлетворительной (приемлемой, допустимой) для игрока А, если

, i = 1,2,..., m,

и удовлетворительной для игрока В,если

,   j = 1,2,..., n.

Ситуация (А _k,B _l) называется равновесной (ситуацией равновесия, устойчивой), или седловой точкой выигрыш-функции игрока А,если она удовлетворительна для каждого из игроков А и В,т.е.

i = 1,2,..., m, j = 1,2,..., n.

или эквивалентным образом

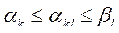
Выигрыш а _kl, соответствующий ситуации равновесия (А _k,B _l), т.е. значение выигрыш-функции игрока A на аргументе (А _k,B _l), называ­ется седловой точкой матрицы игры. Таким образом, элемент а _kl, яв­ляющийся седловой точкой матрицы игры, является минимальным в k -й строке и максимальным в l- м столбце. Игра, матрица которой содержит хотя бы один такой элемент, называется игрой с седловой точкой.

Стратегии A_k и В _l соответственно игроков А и В, создающие равно­весную ситуацию (A_k, В _l), или, другими словами, соответствующие седловой точке а _kl, называются оптимальными. Обозначим через  и  множества чистых оптимальных стратегий соответственно игроков А и В.

Если нижняя цена игры а равна верхней цене игры β, то их общее значение γ = α = β называется ценой игры в чистых стратегиях. Сово­купность  множеств 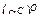 и 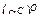 чистых оптимальных стратегий соответственно игроков А и В и цены игры в чистых стратегиях γ называется полным (или общим) решением игры в чистых стратегиях, а совокупность { A_k, В _l, γ} какой-либо пары чистых опти­мальных стратегий A_k, и В _l  и цены игры в чистых стратегиях γ называет­ся частным решением игры в чистых стратегиях.

Теорема. (Критерий существования цены игры в чи­стых стратегиях). Для существования цены игры в чистых стратегиях необходимо и достаточно существование у матрицы этой игры седловой точки.

Теорема. В игре с седловой точкой множество чистых оптимальных стратегий игрока А совпадает с множеством его максиминных стратегий:  , а множество чистых оптимальных стратегий игрока В совпадает с множеством его минимаксных стратегий . В игре без седловой точки ни у одного из игроков нет оптимальных стратегий: , хотя максиминные стратегии игрока А и минимаксные стратегии игрока В всегда существуют .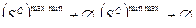

 

Исходя из изложенного, можно сформулировать следующий алго­ритм отыскания седловых точек матрицы игры, оптимальных страте­гий игроков, цены игры и решения игры в чистых стратегиях.

Алгоритм отыскания седловых точек:

1. Находим наименьшие элементы в 1-й строке матрицы игры.

Если ни один из найденных элементов не является наибольшим в столбце, в котором он стоит, то в 1-й строке седловых точек нет.

2. Переходим ко 2-й строке.

Если ни один из наименьших элементов в каждой i- й строке, i = 2,..., т, не является наибольшим в столбце, в котором он стоит, то в i -й строке, i = 2,..., т, седловых точек нет.

Таким образом, матрица игры не имеет седловых точек и, следо­вательно (см. определение оптимальных стратегий и теорему (Критерий существования цены игры в чи­стых стратегиях.) Для существования цены игры в чистых стратегиях необходимо и достаточно существование у матрицы этой игры седловой точки.), у игроков нет оптимальных чистых стратегий, нет цены и решения игры в чистых стратегиях.

3. Если при рассмотрении по строкам первый встречный элемент a _kl наименьший в k -й строке, , оказался наибольшим в l -м столбце, то a _{kl -} седловая точка.

4. Далее, в каждой i -й строке, i = k, k + 1,..., т, начиная с k -й, ищем элементы, числовое значение которых равно числовому зна­чению седловой точки а _kl.   Если     и  ( (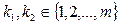; ) — седловые точки,  то  = ). Для каждого найден­ного такого элемента проверяем, является ли он седловой точкой (т.е. наименьшим в строке и наибольшим в столбце, на пересечении которых он стоит).

Таким образом, будут найдены все седловые точки.

5. Стратегии, в соответствующих строках матрицы игры которых стоят седловые точки, являются оптимальными для игрока А. Таким образом, найдено множество .

Стратегии, в соответствующих столбцах матрицы игры которых стоят седловые точки, являются оптимальными для игрока В. Таким образом, найдено множество 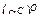. Числовое значение седловой точки есть цена игры в чистых стра­тегиях γ. Общее решение игры имеет вид .

Предложенный метод относится к фундаментальным результатам теории оптимального управления и, как уже это упоминалось выше, имеет важное значение для решения многих более сложных задач, которые, так или иначе, сводятся к простейшей. В то же время очевидны и пределы его эффективного использования, которые целиком зависят от возможности решения задачи.

Метод, основанный на понятии равновесия по Нэшу

 

Определение. Равновесие по Нэшу есть точка 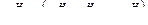 такая, что для всех i = 1,2, …, nдостигается оптимум.

.

Точка m^H     определяется из решения системы уравнений

,   i = 1,2, …, n

Рассмотрим игру 2×2 не имеющий седловой точки

Пусть игрок А использует стратегию А₁  с вероятностью х, а стра­тегию А₂ -  с вероятностью 1 - х.

Пусть игрок B использует стратегию B₁  с вероятностью y, а стра­тегию B₂ -  с вероятностью 1 - y.

Тогда математическое ожидание выигрыша игрока А будет определяться следующим образом:

Заметим, что h_B (x, y)  = - h_A (x, y). Точка Нэша определяется из уравнений

Зная точку Нэша (x^H, y^H), легко можно определить оптимальные стратегии ;  и цену игры v.

Аналитическое решение игры 2×2

Решение матричной игры в чистых стратегиях возможно далеко не всегда. Более типичной является отсутствие седловой точки. Для матричной игры, не имеющей седловой точки, всегда выполняется неравенство v ₁ < v ₂.

Такие игры еще называются неполностью (не вполне) определенными.

Простейшая матричная игра 2×2 определяется матрицей

Если в игре есть седловая точка, то игра имеет решение в чистых стратегиях, иначе она решается в смешанных стратегиях (x ⁰, y ⁰),где ,    причем ; .

По определению оптимальные смешанные стратегии для случая 2×2 могут быть определены из условия .

Если игрок 1 придерживается своей оптимальной стратегии x ⁰, он не получит меньше v при любых стратегиях y игрока 2:

.

Это справедливо, в том числе, если игрок 2 выбирает свои чистые стратегии y = (1,0) и y = (0,1). Для этих двух случаев  имеем:

Выполнение данной системы неравенств возможно в случае

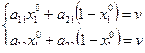
Решая данную систему уравнений, находим

Аналогичные рассуждения приводят к выводу о том, что оптимальная стратегия игрока 2  удовлетворяет системе уравнений

откуда

Таким образом, решение простейшей матричной игры (x ⁰, y ⁰, v)  найдено аналитически.

 

Рассмотрим случай, когда матрица 2×2 - игры не имеет седловой точки.

 

Теорема. Пусть матрица Аразмером 2×2 не имеет седловой точки. Тогда каждый из игроков А и В обладает единственно оптимально смешанной стратегией соответственно  и , где

а цена игры (в смешанных стратегиях) V определяется формулой

 

формулы (т.е. в левых частях этих формул р заменить на q, а в правых частях а заменить на b):

 

теоремы   условие отсутствия у матрицы седловой точки нельзя заменить более слабым условием .

 

Следствие. Если матрица игры Аразмером 2×2  симметрическая, т.е. a ₁₂ = a ₂₁, и не имеет седловой точки, то чистые стратегии A ₁, B ₁  и A ₂, B ₂ входят в соответствующие оптимальные смешанные стратегии  и  соответственно с равными вероятностями: , .

Смешанные оптимальные стратегии   и , фигурирующие в формулировке следствия 3 и 4.

Замечание. Двоякосимметрическая квадратная матрица 2-го порядка не имеет седловых точек, за исключением случая, когда все элементы равны, и в этом случае каждый элемент является седловой точкой.

 

 

Методы решение игр размерности п×п

 

Метод Лагранжа

 

Рассмотрим, каким образом можно определить оптимальные стратегии в игровых задачах размерности п×п методом Лагранжа.

Пусть игра, не имеющая седловой точки и заведомо невыгодных стратегий, описывается квадратной матрицей А размерности п×п:

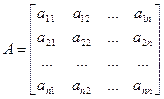
Игрок А использует свои стратегии с вероятностями х₁,..., х _n, а игрок В — с вероятностями у₁,..., у_п, причем , .

Математическое ожидание выигрыша игрока А равно

v = x ^{0 T} A y ⁰

 

где x ^{0 T} = (x ₁,..., х _n), y ^{0 T}  = (y ₁, …, у_п) — оптимальные стратегии игро­ков А и В соответственно.

Следовательно, выигрыш игрока В будет равен (- v). Используем элементы вариационного исчисления и решим за­дачу каждого из игроков методом Лагранжа, составив вспомога­тельные функции       

где λа, λb, — неопределенные множители Лагранжа.

Системы уравнений, дли определения точки Нэша, имеют вид

        

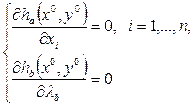
Если подставить значения оптимальных стратегий, полученных из этих соотношений, в выражение для цены игры, получим зна­чение платежа, который игрок А должен получить от игрока В.

Таким образом, цена игры и оптимальные стратегии игроков A и B рассчитывается по выведенным формулам. Предварительно нужно убедится, что нет седловых точек.

⇐ Предыдущая891011121314151617Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: