 |
26. Сколько раз?. 27. Исправить ошибку. 28. Хитроумная головоломка. 30. Сложить метр. 31. Превратить дробь. 32. Волшебный числовой треугольник.
|
|
|
|
26. Сколько раз?
Сколько раз можно прочитать слово «ОРХИДЕЯ» в представленной фигуре?

27. Исправить ошибку.
Берем 12 спичек (палочек) и выкладываем из них «равенство», как показано на рисунке.
Как видите, «равенство» 6—4 не может равняться 9.
Как переложить одну спичку так, чтобы получилось правильное равенство? Задача решается несколькими способами.

28. Хитроумная головоломка.
Из 6 спичек выложите дробь, как показано на рис. Не касаясь других спичек, нужно передвинуть только одну так, чтобы получилась арифметическая дробь равная 1. Спичку, изображающую горизонтальную черту дроби, двигать нельзя.
29. Жук.
На рисунке изображен «жук» из 10 спичек (счетных палочек). Необходимо изменить направление движения жука, переложив всего три спички (счетные палочки).

30. Сложить метр.
Каждая из имеющихся 13 спичек имеет длину 4, 5 см. Как из них сложить метр?
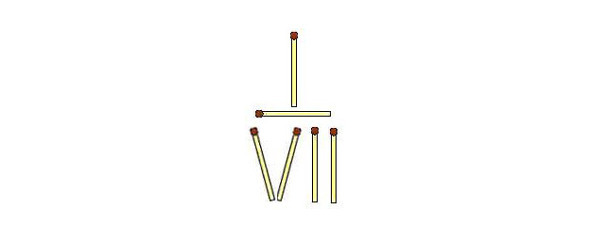
31. Превратить дробь.
На рисунке из семи спичек выложено число 1/7. Переложив всего одну спичку нужно превратить эту дробь в число 1/3. Попробуйте!

32. Волшебный числовой треугольник.
В вершинах треугольника помещены числа 1, 2 и 3. Разместите числа 4, 5, 6, 7, 8 и 9 по сторонам треугольника (по две цифры на каждой стороне) так, чтобы сумма всех чисел вдоль каждой стороны треугольника равнялась 17. Это нетрудно, так как известны числа в вершинах треугольника.
А сейчас попробуйте разместить числа 1, 2, 3, 4, 5, 6, 7, 8 и 9 вдоль сторон треугольника (по четыре цифры на стороне) так, чтобы сумма чисел на каждой стороне треугольника равнялась 20.
Числа в вершинах треугольника будут другие. В первом и втором случаях числа не повторяются и должны размещаться только по одному разу. Расположение чисел по сторонам треугольника может быть разнообразным.
|
|
|

33. Сколько стоит книга?
За книгу заплатили 1 рубль и еще половину стоимости книги. Сколько стоит книга?
34. Шутка.
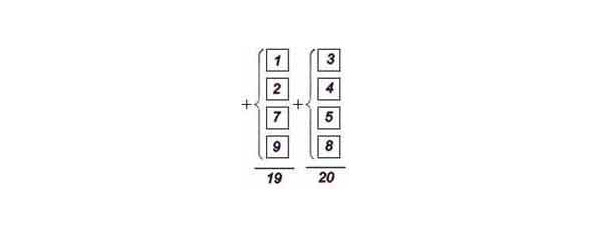
Приготовьте 8 квадратов с числами 1, 2, 3, 4, 5, 6, 7, 8 и 9 и расположите их в два столбца, как показано на рисунке. Необходимо переместить всего два квадрата и добиться того, чтобы сумма чисел в обоих столбцах была одинаковой.
35. Три в ряд.
Расположите на столе 9 шашек в форме квадрата по 3 шашки на каждой стороне и одну в центре. Если вдоль какой-нибудь прямой линии располагаются две шашки или более, то такое расположение мы будем называть «рядом». Так, АВ и СD ряды, в каждом из которых по 3 шашки в каждом, а ЕF – ряд содержащий две шашки.

Необходимо определить, сколько на рисунке всего рядов по 3 шашки в каждом и сколько таких рядов, в каждом из которых только по 2 шашки.
А теперь необходимо убрать 3 любые шашки, а оставшиеся 6 расположить в 3 ряда так, чтобы в каждом ряду было по 3 шашки.
36. Десять рядов.
Нетрудно догадаться, как расположить 16 шашек в 10 рядов по 4 шашки в каждом ряду. Гораздо труднее расположить 9 шашек в 10 рядов так, чтобы в каждом ряду было по три шашки.
Попробуйте решить обе задачи.
37. Из «кувшина» – квадрат.
Перерисуйте на лист бумаги фигуру, имеющую форму кувшина, и разрежьте ее двумя прямолинейными разрезами на такие 3 части, из которых можно было бы сложить квадрат.

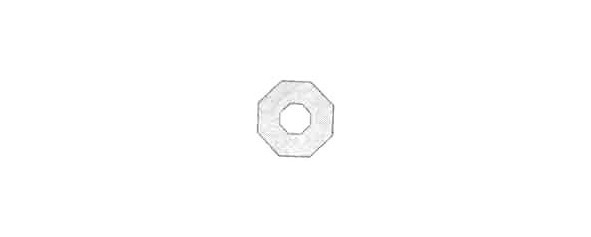
38. Красивое превращение.
Перерисуйте на тонкий картон или плотную бумагу изображенный на рисунке правильный восьмиугольник и в центре вырежьте отверстие тоже в форме правильного восьмиугольника. Образовавшуюся фигуру требуется разрезать на 8 равных частей и, перекладывая их составить восьмиконечную звезду, которая бы также имела восьмиугольное отверстие.
|
|
|
|
|
|


