 |
П.5. Итерационный метод (метод Брауна – Робинсона)
|
|
|
|
Предмет теории игр
Практически в любой отрасли человеческой деятельности возникают конфликты, то есть ситуации, при которых сталкиваются стороны с несовпадающими интересами. Естественно, что каждой из конфликтующих сторон интересно выработать стратегию поведения, приносящую максимальную выгоду. Решение такой задачи, как правило, осложняется тем, что конфликтующая сторона не имеет полной информации о конфликте в целом. Это может быть связано с сознательным стремлением противника скрыть свои планы или с тем, что в качестве противника выступает случайный фактор и т.д. Зачастую говорят, что в конфликтной ситуации требуется выбрать оптимальное решение в условиях неопределенности.
Подобные задачи можно решать, используя аппарат математического моделирования. Математическая модель конфликтной ситуации называется игрой.
Теория игр – раздел исследования операций, предметом которого является выработка оптимальных решений в условиях неопределенности.
Первые попытки составить математические модели конфликтных ситуаций предпринимались еще в XVII в. Систематическое изложение математических основ теории игр было дано в работе Дж. Неймана и О. Моргенштерна «Теория игр и экономическое поведение» (1944 г).
К настоящему времени теория игр превратилась в развитую теорию, которая находит многочисленные приложения в задачах управления, планирования, прогнозирования и т.д. Особое значение теория игр приобретает в конкурентной рыночной экономике.
Надо заметить, что хотя теория игр и занимается выработкой целесообразных решений в конфликтной ситуации, но она не рассматривает конструктивного аспекта конфликта и не прогнозирует последствия конфликта.
|
|
|
Часть своей терминологии теория игр позаимствовала у так называемых салонных игр (шахматы, шашки, карточные игры и т.д.).
Стороны конфликта будем в дальнейшем называть игроками, действие игрока – ходом, совокупность ходов – стратегией, результат игры – выигрышем и т.д.
В теории игр считается обязательным до начала игры оговорить ее правила. В правила игры обычно входят совокупность требований и ограничений на действия игроков, обмен информацией игроков о действиях противников, функции выигрышей игроков, описание начальной и финальной позиций и т.д. Правила должны быть четкие, иначе игра не состоится.
Поскольку теория игр является разделом исследования операций, то математическая модель конфликтной ситуации должна состоять из двух частей.
Первая часть – целевые функции, которые надо оптимизировать, вторая часть – система ограничений. В данном случае система ограничений оговаривается правилами игры. Целевые функции могут быть самыми разнообразными. Они определяются самими игроками и могут меняться от игры к игре.
К настоящему времени существует несколько способов классификации игр. В данной работе основное внимание уделяется бескоалиционным конечным парным играм с выигрышами, а именно: матричным играм, позиционным играм, биматричным играм и коалиционным играм.
Матричные игры
П.1. Основные понятия теории матричных игр
Пусть в игре участвуют два игрока А и В. Назовем одного из них (например игрока А) «нападающим», другого – «защитником». Игроки одновременно делают по одному ходу. Заметим, что в этом случае понятие хода совпадает с понятием стратегии. Пусть игрок А может выбрать одну из стратегий А1, А2, …, Аm, игрок В – одну из стратегий В1, В2, …, Вn.
Будем полагать, что интересы игроков противоположны, т.е. при выборе нападающим стратегии i, а защитником – стратегии j выигрыш нападающего и проигрыш защитника составит одну и ту же величину аij.
|
|
|
Все взаимные выигрыши нападающего и проигрыши защитника можно задать с помощью одной матрицы
 . (6.1)
. (6.1)
Такую матрицу часто называют платежной матрицей. Данная матрица и дала название описанному типу игр – матричные игры. Матричные игры называют играми с нулевой суммой, поскольку, суммарный выигрыш игроков всегда будет равен нулю. Будем полагать, что нападающий может выбрать независимо от защитника любую из m строк платежной матрицы, защитник – один из n столбцов. Выбор строки или столбца игроком составит стратегию игрока.
Проиллюстрируем на несложном примере принципы построения платежной матрицы.
П р и м е р 2.1. Руководитель торговой фирмы решает вопрос о том, какое количество саженцев ему следует закупить к сезону. К покупке товара он может прибегнуть лишь один раз. Каждый саженец стоит 2 ден.ед. и может быть продан за 4 ден.ед. Саженцы, оставшиеся нераспроданными к концу сезона, полностью обесцениваются и никакой стоимости не представляют. Известно, что количество саженцев, которое может быть продано, колеблется от 1 до 4. Составить матрицу денежных сумм, полученных в зависимости от решения руководителя фирмы и от результатов продажи. Номеру строки соответствует решение руководителя фирмы о количестве закупаемых саженцев, а номеру столбца – количество проданных саженцев.
Решение. Элементы матрицы денежных сумм, полученных в результате продажи, определим по формулам
aij = 4j – 2i, если j £ i,
aij = 2i, если j > i, где i = 1, 2, 3, 4, j = 1, 2, 3, 4.
Например, а31 соответствует решению руководителя о покупке 3-х саженцев по 2 ден.ед. при спросе рынка всего на один саженец. а31 = 4 × 1 – 2 × 3 = – 2, т.е. предложение выше спроса, и в этом случае фирма несет убыток 2 ден.ед. а24 соответствует решению о покупке 2-х саженцев, когда спрос будет на четыре: а24 = 2 × 2 = 4 (нельзя продать больше, чем имеешь). В этом случае фирма получит прибыль. Диагональные элементы матрицы денежных сумм соответствуют равенству спроса и предложения: а44 – четыре саженца куплено и 4 продано, а44 = 4 × 4 – 2 × 4 = 8. Таким образом,
 .5
.5
П.2. Игры с природой
Рассмотрим матричную игру, в которой в качестве одного из игроков выступает неопределенный фактор. Такую игру называют игрой с природой.
|
|
|
Как уже говорилось, теорию игр можно охарактеризовать как теорию принятия оптимальных решений в условиях неопределенности. В играх с природой неопределенность будет обусловлена действием случайного фактора.
Обычно принято полагать, что природа является защитником, следовательно, может выбирать любой из столбцов платежной матрицы. Все рекомендации данного пункта будут, естественно, относиться к нападающему.
На практике платежные матрицы достигают значительных размеров. Перед началом игры целесообразно отбросить некоторые стратегии.
Нападающий, имеющий цель выиграть как можно больше, может отбросить те стратегии, которые дают заведомо меньший выигрыш. Это означает, что из платежной матрицы можно вычеркнуть ту строку (i), элементы которой не больше соответствующих элементов какой-либо другой строки (k). При этом говорят, что строка k доминирует строку i.
Поскольку природа не желает обыграть нападающего, то сократить количество стратегий-столбцов нельзя.
Поясним процесс уменьшения числа стратегий на примере.
П р и м е р 2.2. Провести сужение стратегий в игре с природой, заданной матрицей
А =  . (6.2)
. (6.2)
Решение. Поскольку все элементы стратегии А4 не превосходят соответствующих элементов стратегии А3, то четвертую строку матрицы можно вычеркнуть. Получим
А =  .5 (6.3)
.5 (6.3)
Существует ряд критериев для выбора наилучшей в определенном смысле стратегии для нападающего.
1. Критерий Лапласа. Основная идея критерия Лапласа состоит в том, что надо выбрать ту стратегию, для которой математическое ожидание будет больше.
П р и м е р 2.2 (продолжение). Предположим, что нападающему известно поведение природы, заданное распределением вероятностей
Таблица 2.1.
| Bj | В1 | В2 | В3 | В4 | ||
| qj | 1/8 | 1/3 | 3/8 | 1/6 |
Необходимо выбрать оптимальную стратегию для нападающего.
Решение. Рассчитаем математическое ожидание выигрышей относительно каждой стратегии по строкам.
 ;
;
 ;
;
 .
.
Поскольку математическое ожидание выигрыша при стратегии А3 наибольшее, то следует отдать ей предпочтение. 5
|
|
|
Очевидно, что для того, чтобы получить закон распределения вероятностей в реальных условиях необходимо собрать достаточный объем статистических данных. Зачастую именно сбор статистических данных становится трудновыполнимой задачей. Это связано с тем, что экономические эксперименты на предприятиях достаточно дороги. Большинство предприятий (особенно сельскохозяйственных) обладает яркой индивидуальностью из-за климатических условий, менталитета населения и т.д., поэтому не всегда можно безоглядно пользоваться опытом других предприятий.
В случае, когда распределение вероятностей неизвестно, можно воспользоваться критерием Лапласа, считая все состояния природы равновероятными.
П р и м е р 2.2 (продолжение). Найти с помощью критерия Лапласа оптимальную стратегию в случае, когда распределение вероятностей неизвестно.
Решение. Считаем все состояния природы равновероятными, т.е.
Таблица 2.2.
| Bj | В1 | В2 | В3 | В4 | ||
| qj | 1/4 | 1/4 | 1/4 | 1/4 |
Рассчитаем математические ожидания выигрышей.
 ;
;
 ;
;
 .
.
Наиболее выгодной является первая стратегия. 5
2. Критерий Вальда. Иногда возникают ситуации, когда невозможно даже приблизительно оценить вероятности состояний природы. Плюс к этому проигрыш влечет за собой достаточно тяжкие последствия. В таких случаях принято искать не лучшее решение, а лучшее из худших. Такая позиция отличается осторожностью и разумным пессимизмом. Одно и другое совсем не лишнее в экономике.
Основное предположение, которого будем придерживаться, – природа враждебна для нападающего, т.е. в любой ситуации она попытается нанести максимальный вред.
Критерии, основанные на данном предположении, называются пессимистическими критериями. Одним из таких критериев называется максиминный критерий Вальда.
Согласно этому критерию оптимальной стратегией считается та, при которой гарантированный выигрыш в любом случае будет не меньше, чем «нижняя цена игры с природой».
 . (6.4)
. (6.4)
Поясним критерий Вальда на примере.
П р и м е р 2.2 (продолжение). Используя критерий Вальда, определить оптимальную стратегию в игре с природой.
Решение. Определим минимальные выигрыши по строкам и выберем ту стратегию, при которой минимум строки максимален.
 .
.
В данном случае это первая стратегия (А1), для которой  . 5
. 5
3. Критерий Севиджа. В критерии Вальда при выборе оптимальной стратегии использовалась только платежная матрица А. В этом случае достоинства любого решения будут описываться несколько однобоко. В критерии Вальда нападающий пытается подстроиться под природу, практически не думая о собственных действиях. Поясним данное высказывание. Предположим, что выигрыш aij больше выигрыша akm. Однако, однозначно заявить, что стратегия Аi лучше, чем стратегия Аk нельзя, поскольку многое зависит от состояния природы. Вполне можно считать, что состояние природы Bj больше нас устраивает, чем состояние Bm. Не секрет, что при благоприятных погодных условиях даже средний фермер способен собрать приличный урожай, в случае же засухи или проливных дождей «битву за урожай» может проиграть самый опытный специалист. Поэтому размер выигрыша еще не повод славить первого и ругать второго. Быть может, последний сделал все, что было возможно в неблагоприятных для него условиях, а первый мог упустить свой более счастливый шанс.
|
|
|
Для того чтобы оценить удачность или неудачность выбора стратегии в определенных условиях, вводится матрица рисков.
Пусть природа находится в состоянии Bj, т.е. она «выбрала» j-й столбец платежной матрицы. Для нападающего наиболее удачной будет стратегия Аi, при которой выигрыш окажется максимальным. Пусть  . При других стратегиях игрок будет терять какую-то часть выигрыша именно из-за своих неудачных действий. Величину такой потери назовем риском. Чтобы получить риск rij, нужно из bj вычесть фактический выигрыш аij:
. При других стратегиях игрок будет терять какую-то часть выигрыша именно из-за своих неудачных действий. Величину такой потери назовем риском. Чтобы получить риск rij, нужно из bj вычесть фактический выигрыш аij:
rij = bj – аij. (6.5)
П р и м е р 2.2 (продолжение). Составить по данной платежной матрице матрицу рисков.
Решение.

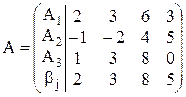 .
.
 .
.
Матрица рисков дает нам дополнительную информацию о данной игре с природой. В платежной матрице А в первой строке второй и четвертый элементы равны между собой а12 = а14 = 3, однако с точки зрения удачности выбора стратегии эти выигрыши неравноценны. При состоянии природы В2 стратегия А1 была оптимальной, а вот при состоянии природы В4 стратегия А1 хуже стратегии А2 на целых две единицы, т.е. выбор стратегии А1 нельзя назвать удачным (r12 = 0, r14 = 2). 5
Говорят, что риск – это плата за отсутствие информации. Естественно, следует выбрать такую стратегию, которая свела бы риск к минимуму. Один из методов избежать чрезмерного риска дает минимаксный критерий Севиджа. Этот критерий относится к пессимистическим критериям, но в отличие от критерия Вальда предполагает работу не с платежной матрицей, а с матрицей рисков.
Оптимальной в данном случае выбирается та стратегия, при которой величина максимального риска минимальна:
 . (6.6)
. (6.6)
П р и м е р 2.2 (продолжение). Используя минимаксный критерий Севиджа определить оптимальную стратегию для нападающего.
Решение. В каждой строке рисков найдем максимальное значение. Из них выбираем минимальное.
 .
.
Из чисел правого столбца значение  , что соответствует стратегии А1. Значит она является оптимальной, согласно критерию Севиджа. 5
, что соответствует стратегии А1. Значит она является оптимальной, согласно критерию Севиджа. 5
Надо отметить, что стратегия, оптимальная по критерию Вальда, не обязательно оптимальна по критерию Севиджа.
Заметим также, что понятия риска можно использовать при оценке целесообразности эксперимента. Можно показать [3], что эксперимент имеет смысл проводить только в том случае, когда его стоимость меньше минимального среднего риска.
4. Критерий Гурвица. Этот критерий учитывает как пессимистический, так и оптимистический подходы.
Согласно критерию Гурвица, оптимальная стратегия выбирается из условия
 . (6.7)
. (6.7)
Здесь l - «коэффициент пессимизма», причем 0 £ l £ 1. При l = 1 критерий Гурвица переходит в критерий Вальда. При l = 0 – в критерий «крайнего оптимизма», при котором выбирается стратегия-строка с максимальным выигрышем.
Значение l выбирается из субъективных соображений для каждой конкретной задачи. Вообще говоря, выбор l является отдельной и далеко непростой задачей.
П р и м е р 2.2 (продолжение). Используя критерий Гурвица (l = 0,4) определить оптимальную стратегию в игре с природой.
Решение. В каждой строке платежной матрицы выберем наибольшее и наименьшее значения и проведем расчеты согласно уравнениям (6.7).
Н1 = 2 × 0,4 + 6 × 0,6 = 4,4;
Н2 = -2 × 0,4 + 5 × 0,6 = 2,2;
Н3 = 0 × 0,4 + 8 × 0,6 = 4,8.
Максимальное значение Hj (j = 1, 2, 3) соответствует третьей стратегии. Она и является оптимальной, согласно критерию Гурвица, при данном значении l.5
Как видно из проведенных исследований для игры с природой, заданной платежной матрицей (6.2), в случае осторожного поведения предпочтительна стратегия А1. В случае же, если есть основания надеяться на благоприятное поведение природы, можно предпочесть стратегию А3.
Можно применить критерий Гурвица для игры с природой, используя матрицу рисков.
П.3. Стратегические игры
В данном пункте разберем случай, когда оба участника матричной игры обладают интеллектом и имеют желание обеспечить себе наилучший исход игры. Здесь уже нельзя применять рассуждения, основанные на том, что противник тебя «помилует». Такие игры, в отличие от игр с природой, могут дать более конкретные рекомендации, т.е. игра является более определенной.
Как и раньше, будем одного из игроков именовать «нападающим» и предоставим ему выбирать строки платежной матрицы, другого игрока назовем «защитником» и отдадим ему власть над столбцами. Однако защитник теперь действует целенаправленно и готов дать «бой» нападающему.
Название вида матричной игры зависит от вида неопределенности, заложенной в ее основу. В данном случае игроки сознательно не информируют друг друга о своей стратегии. Поэтому такой вид игры называется стратегической игрой.
Введем понятие нижней и верхней границы игры. Для этого рассмотрим точку зрения нападающего. В стратегической игре у игрока А нет оснований рассчитывать на доброе отношение защитника. Следовательно, он должен придерживаться осторожной тактики поведения. С этим мы уже встречались при изучении критерия Вальда. То есть, нападающий должен выбрать в каждой стратегии наихудший вариант, а из них – наилучший. Полученное значение называется нижней границей игры или максимальным гарантированным выигрышем нападающего. Традиционно нижняя граница обозначается через a.
 . (6.8)
. (6.8)
Теперь поставим себя на место защитника. Его задача свести свой проигрыш к минимуму в условиях, когда его противник стремится нанести ему максимальный вред. Следовательно, ему надо придерживаться осторожной минимаксной стратегии, т.е. в каждом столбце платежной матрицы следует определить максимальный элемент, а из них следует выбрать минимальный. Полученное значение принято называть верхней границей игры или гарантированным наименьшим проигрышем (b).
 . (6.9)
. (6.9)
В случае если a = b, считается, что игра имеет седловую точку. Такая игра определена в том смысле, что ни одному игроку не выгодно отклоняться от своей осторожной стратегии. Нападающий, выбрав максиминную стратегию, получит выигрыш v = a = b, защитник – такой же по величине проигрыш.
Рассмотрим следующий пример.
П р и м е р 2.3. Определить верхнюю и нижнюю цену игры, заданной платежной матрицей
 .
.
Решение. Составим таблицу
| В1 | В2 | В3 | минимум по строкам | |||
| А1 | ||||||
| А2 | ||||||
| А3 | ||||||
| максимум по столбцам |
1) Выбираем в каждой строке наименьший элемент, из них выбираем наибольший: a = 5.
2) Выбираем в каждом столбце наибольший элемент, из них возьмем наименьший: b = 5.
Получим a = b = 5.
Рекомендуется игроку А придерживаться стратегии А3, игроку В – стратегии В2. Такое поведение устроит обоих противников, и в игре будет достигнуто равновесие. 5
В данном случае стратегии игроков определены однозначно, а игра называется игрой в чистых стратегиях.
Действительно, пусть игрок А, прельщенный возможным максимальным выигрышем а13 = 10, выбирает первую стратегию. В этом случае защитник, оставаясь верным своей осторожной стратегии В2, уменьшит свой проигрыш на единицу (а12 = 4). Аналогичный анализ можно провести относительно действий защитника.
Таким образом, в случае наличия седловой точки, матричная игра перестает быть игрой, как таковой, поскольку исчезает неопределенность в действиях противников.
Пусть b > a. Выигрыш (v) будет удовлетворять условию: a < v < b.
В этом случае имеется возможность каждому из игроков побороться за лучший исход, чем тот, который гарантирует ему осторожная (максиминная или минимаксная) стратегия.
Введем понятие смешанной стратегии. Предположим, что каждый из игроков применяет какую-то выбранную им стратегию с определенной вероятностью. Например, игрок А выбирает свои стратегии А1, А2, …, Аm с вероятностями р1, р2, …, рm ( ), игрок В выбирает свои стратегии В1, В2, …, Вn с вероятностями q1, q2, …, qn (
), игрок В выбирает свои стратегии В1, В2, …, Вn с вероятностями q1, q2, …, qn ( ) соответственно. В этом случае говорят, что в игре применяются смешанные стратегии.
) соответственно. В этом случае говорят, что в игре применяются смешанные стратегии.
Заметим, что применять смешанные стратегии имеет смысл в том случае, когда матричная игра проводится несколько раз.
В смешанных стратегиях игроки, в принципе, продолжают придерживаться осторожных стратегий, однако смысл их немного меняется.
Нападающий стремится так подобрать смешанные стратегии, т.е. составить закон распределения вероятностей  ,
,  , …,
, …,  , чтобы обеспечить себе максимальное из минимальных математическое ожидание выигрыша (v*), т.е.
, чтобы обеспечить себе максимальное из минимальных математическое ожидание выигрыша (v*), т.е.
 . (6.10)
. (6.10)
Защитник придерживается стратегии минимакса. Максимально возможное математическое ожидание его проигрыша (v*) определяется соотношением
 . (6.11)
. (6.11)
Если оптимальные стратегии для обоих игроков найдены, то оптимальный ожидаемый выигрыш в матричной игре определяется соотношением
 . (6.12)
. (6.12)
Как и в случае чистых стратегий, справедливо соотношение
v* £ v*.
Сформулируем основную теорему матричных игр.
Теорема 2.1 (теорема фон Неймана). Каждая конечная игра с нулевой суммой имеет, по крайней мере, одно оптимальное решение среди смешанных стратегий.
Для упрощения поиска решения стратегической игры полезно предварительно уменьшить количество стратегий, пользуясь методом доминирования.
П р и м е р 2.4. Используя принцип доминирующих стратегий, сузить размер игры, заданной матрицей
 .
.
Определить нижнюю и верхнюю границу игры.
Решение. Начнем с нападающего. В данной матрице все элементы первой строки не меньше, чем элементы третьей. Следовательно, нападающему не следует выбирать стратегию А3, которую отбрасываем. Получим
 .
.
В свою очередь защитнику следует избегать четвертой стратегии, поскольку его проигрыш будет большим, чем при стратегии В3 или В2.
Получим
 .
.
Больше ни одну стратегию убрать нельзя.
Определим нижнюю и верхнюю границы игры.
a = max (0; 1) = 1;
b = min (3; 3; 2) = 2.
Значит, 1 £ v £ 2, т.е. данная игра неопределенная. 5
На данный момент существует несколько методов решения матричных игр в смешанных стратегиях.
П.4. Сведение матричной игры к задаче линейного
программирования
Данный метод был предложен Дж. фон Нейманом (1947 г.).
В п. 3 упоминалось, что цель нападающего подобрать так распределение вероятностей р1, р2, …, рm, чтобы обеспечить себе математическое ожидание выигрыша не менее определенной величины v, т.е.
 . (6.13)
. (6.13)
Условия (6.13) можно переписать следующим образом
 (6.14)
(6.14)
Добавим к условиям (6.14) условия нормировки и неотрицательности вероятностей (р1 + р2 + … + рm = 1, pj ³ 0 (j = 1, …, m)). Получим систему для определения оптимальной смешанной стратегии для нападающего.
Сформулируем задачу.
Требуется подобрать вероятности р1, р2, …, рm так, чтобы обеспечить максимальное значение математического ожидания выигрыша (v ® max) при ограничениях:
р1 + р2 + … + рm = 1.
 (6.15)
(6.15)
Аналогично получим оптимизационную задачу для защитника. Требуется найти распределение вероятностей q1, q2, …, qn так, чтобы минимизировать математическое ожидание проигрыша (v ® min), при ограничениях:
q1 + q2 + … + qn = 1.
 (6.16)
(6.16)
Можно заметить, что условия (6.15) и (6.16) схожи с условиями задачи линейного программирования. Чтобы свести их к задаче линейного программирования, поступим следующим образом.
Предположим, что v > 0. Если это не так, можно воспользоваться следующим утверждением.
Теорема 2.2 (об аффинности матричных игр). Если к каждому элементу платежной матрицы прибавить или отнять какое-либо число, то и математическое ожидание выигрыша изменится на такое же число.
Итак, считаем, что v > 0. Разделим обе части системы (6.15) на v и введем новые переменные  . Получим
. Получим
t1 + t2 + … + tm =  .
.

Учитывая, что задача нападающего максимизировать свой выигрыш, т.е.
v ® max, получим:
Z =  = t1 + t2 + … + tm ® min.
= t1 + t2 + … + tm ® min.
Таким образом, матричная игра для нападающего сведена к стандартной задаче линейного программирования на минимум.
Аналогично для защитника можно получить
f =  = t1 + t2 + … + tn ® max,
= t1 + t2 + … + tn ® max,
 (6.18)
(6.18)
Здесь  .
.
Заметим, что задачи (6.17) и (6.18) являются двойственными задачами линейного программирования.
П р и м е р 2.4 (продолжение). Свести матричную игру к задаче линейного программирования.
Решение. После отбрасывания заведомо проигрышных стратегий платежная матрица приняла вид:
 .
.
Встанем на позицию защитника.
Пусть q1, q2, q3 – вероятности, с которыми защитник выбирает стратегии В1, В2, В3 соответственно. Для данного примера система (6.16) примет вид:
q1 + q2 + q3 = 1,
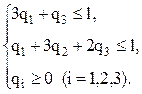
Введем новые переменные
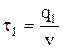 ,
,  ,
, 
Получим задачу линейного программирования:
f = t1 + t2 + t3 ® max,
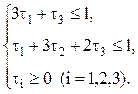
Решим задачу симплексным методом.
Таблица 2.3.
| Базис | Сбазиса | А0 | С1 = 1 | С2 = 1 | С3 = 0 | С4 = 0 | С5 = 0 | |
| А1 | А2 | А3 | А4 | А5 | ||||
| А4 | ||||||||
| А5 | ||||||||
| Zj – Cj | – 1 | – 1 | – 1 | |||||
| А4 | 1/2 | 5/2 | – 3/2 | – 1/2 | ||||
| А3 | 1/2 | 1/2 | 3/2 | 1/2 | ||||
| Zj – Cj | 1/2 | – 1/2 | 1/2 | 1/2 | ||||
| А1 | 1/5 | – 3/5 | 2/5 | – 1/5 | ||||
| А3 | 2/5 | 21/10 | – 1/5 | 3/5 | ||||
| Zj – Cj | 3/5 | 1/2 | 1/5 | 2/5 | ||||
Таким образом, решение исходной задачи линейного программирования:
fmax = 3/5, t1 = 1/5, t2 = 0, t3 = 2/5.
Решение двойственной задачи:
Zmin = fmax = 3/5, t1 = 1/5, t2 = 2/5,
получим из решения задачи линейного программирования
Решение матричной игры:
 .
.
Заметим, что 1 £  £ 2.
£ 2.
q1 = t1 × v =  .
.
q2 = t2 × v = 0.
q3 = 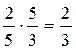 .
.
Значит, для того, чтобы математическое ожидание проигрыша для защитника не превышало  у.е., ему нужно с вероятностью 1/3 выбрать первую стратегию, с вероятностью 2/3 – вторую стратегию и третью не выбирать.
у.е., ему нужно с вероятностью 1/3 выбрать первую стратегию, с вероятностью 2/3 – вторую стратегию и третью не выбирать.
Для нападающего оптимальное распределение вероятностей имеет вид:
р1 = 1/3, р2 = 2/3. 5
П.5. Итерационный метод (метод Брауна – Робинсона)
Данный метод отличается достаточной простотой. Суть его в том, что матричная игра проводится несколько раз, при этом, естественно, накапливаются статистические данные об игре. По ним и вырабатываются рекомендации для игроков.
Продемонстрируем работу итерационного метода на примере.
П р и м е р 2.4 (продолжение). Определить математическое ожидание выигрыша и оптимальные смешанные стратегии игроков в игре, заданной платежной матрицей
 .
.
Решение. Первый тур. Предоставим право первого хода нападающему, т.е. игроку А. В его распоряжении две стратегии А1 – (3, 0, 1) и А2 – (1, 3, 2). Зная, что за его ходом последует ответный «удар» игрока В, нападающий выберет стратегию А2, где находится максимальный из минимальных выигрышей (выделенный элемент).
Наступает время для ответного хода игрока В. Тот, желая отбиться от нападающего, выбирает первую стратегию В1. В результате своей атаки игрок А получил максимальный гарантированный выигрыш v* = 1. Теперь вновь его ход. Поскольку игрок В выбрал первую стратегию, то перед игроком А следующая картина возможных выигрышей – 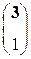 . Естественно, игрок А выбирает первую стратегию, получая выигрыш v* = 3. При этом средний выигрыш за первый тур игры можно определить следующим образом:
. Естественно, игрок А выбирает первую стратегию, получая выигрыш v* = 3. При этом средний выигрыш за первый тур игры можно определить следующим образом:
 .
.
Начинается второй тур игры. Накопленный опыт игроков в данном случае будет проявляться в накопленных выигрышах в результате той или иной стратегии. Игрок А выбрал стратегию А1 и его накопленные выигрыши за два хода составят – (1, 3, 2) + (3, 0, 1) = (4, 3, 3). Минимизируя свой проигрыш, игрок В может на свое усмотрение выбрать либо стратегию В2, либо В3. Пусть ему приглянулась стратегия В2. В этом случае его накопленный проигрыш за два хода составит 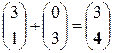 . Максимизируя свой выигрыш, игрок А выберет стратегию А2.
. Максимизируя свой выигрыш, игрок А выберет стратегию А2.
Средний выигрыш за два хода определим следующим образом:
 ;
; 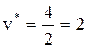 ;
;  .
.
И т.д.
Результаты игры удобно заносить в таблицу (см. 2.4). Поясним кратко ее устройство.
1-й столбец – номер итерации;
2-й столбец – номер стратегии, выбранной игроком А;
3-й столбец – накопленный в результате n ходов проигрыш игрока В, придерживающегося стратегии В1;
4-й столбец – накопленный в результате n ходов проигрыш игрока В, придерживающегося стратегии В2;
5-й столбец – накопленный в результате n ходов проигрыш игрока В, придерживающегося стратегии В3;
6-й столбец – номер стратегии, выбранной игроком В;
7-й столбец – накопленный игроком А выигрыш при стратегии А1;
8-й столбец – накопленный игроком А выигрыш при стратегии А2;
9-й столбец – нижняя граница игры, равная минимальному накопленному проигрышу по стратегиям В1, В2, В3, деленная на число ходов;
10-й столбец – верхняя граница игры, равная максимальному накопленному выигрышу по стратегиям А1, А2, деленная на число ходов;
11-й столбец – средний выигрыш  .
.
| n | i | B1 | B2 | B3 | j | A1 | A2 | v* | v* | v |
| 1,5 | 1,75 | |||||||||
| 1,5 | ||||||||||
| 1,5 | 1,75 | |||||||||
| 1,6 | 1,8 | |||||||||
| 1,67 | 1,83 | 1,75 | ||||||||
| 1,57 | 1,71 | 1,64 | ||||||||
| 1,625 | 1,75 | 1,69 | ||||||||
| 1,67 | 1,78 | 1,72 | ||||||||
| 1,6 | 1,7 | 1,65 |
Заметим, что иногда (см., например, 2-ю итерацию) появляется несколько одинаково хороших стратегий (В2, В3), в этом случае стратегия выбирается произвольно.
Запишем результат, полученный после десяти итераций:
v = 1, 65
(сравните с точным результатом  ).
).
Игрок А воспользовался стратегией А1 3 раза, А2 – 7 раз, т.е. р1 = 0,3; р2 = 0,7 (точные значения р1 = 1/3» 0,33, р2 = 2/3» 0,67).
Аналогично, для игрока В. q1 = 0,4; q2 = 0,1; q3 = 0,5 (точные значения q1 = 1/3» 0,33, q2 = 0, q3 = 2/3» 0,67). 5
Как видно, после всего десяти итераций можно уже судить об основных тенденциях игры.
Вообще, итерационный метод сходится достаточно медленно, поэтому существуют методы «ускоряющие его».
Главное достоинство метода итераций в том, что его сложность, в отличие от симплексного метода, мало возрастает при увеличении платежной матрицы.
|
|
|


