П.2. Нечеткая игровая модель с проведением изучающего эксперимента

 

Нечеткая игровая модель с единичным экспериментом. В данном случае основные предпосылки и формальная постановка задачи практически идентичны рассмотренным в разделе 2.1.1, за тем исключением, что степени уверенности γ_j о выборе игроком 2 того или иного варианта действий задаются не в результате определенной экспертной процедуры, а на основании изучающего эксперимента, в процессе которого фиксируется набор признаков {x_k}, среди которых могут быть как количественные (непрерывные), так и качественные (дискретные);

Поскольку общие этапы нахождения решения нечеткой матричной игры (в случае нескольких критериев) были рассмотрены выше, здесь основной задачей является нахождение набора функций принадлежности g_jk(x_k), отражающих степени уверенности, что при фактически наблюдаемом признаке 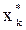игроком 2 будет избран вариант поведения B_j.

Постановка задачи. Пусть b_jk – некоторый терм, отображаемый совокупностью пар (т. е. как нечеткое множество):

 

, (6.25)

 

где – универсальное множество, на котором задается нечеткое множество b_jk; 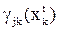– степень принадлежности элемента нечеткому множеству b_jk.

Задача состоит в том, чтобы определить 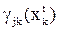для всех . Совокупность этих значений и будет составлять неизвестную функцию принадлежности.

Основные определения и соотношения. Метод, который предлагается для решения поставленной задачи, базируется на идее распределения степеней принадлежности элементов универсального множества согласно с их рангами. В данном случае под рангом элемента будем понимать число , которое характеризует значимость этого элемента в формировании свойства, которое описывается нечетким термом b_jk.Предполагается, что чем больше ранг элемента, тем больше степень принадлежности.

Отметим, что с учетом этого предположения и при введении обозначений (индексы k и jдля упрощения записей опускаем):

 

,

 

правило распределения степеней принадлежности можно задать в виде соотношения:

, (6.26)

 

к которому (для получения затем однозначного решения) добавим условие нормировки

. (6.27)

 

Используя (6.26), легко определить степени принадлежности всех элементов универсального множества через степень принадлежности опорного элемента.

Если опорным является элемент x_k¹ÎW _k с принадлежностью g₁, то

 

. (6.28)

 

Для опорного элемента с принадлежностью получаем:

 

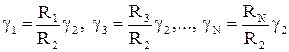. (6.29)

 

И, наконец, для опорного элемента с принадлежностью имеем:

 

. (6.30)

 

Учитывая условия нормировки (6.27), из соотношений (6.28)-(6.30) находим:

 

(6.31)

 

Полученные формулы (6.31) дают возможность вычислить степени принадлежности 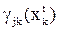элементов к нечеткому терму b_jk двумя независимыми путями:

1) по абсолютным оценкам уровней , которые определяются согласно методикам, предложенных в монографии [15]. Для экспертных оценок рангов, как и ранее, можно использовать 9-бальную шкалу (1 – наименьший ранг, 9 – наибольший ранг).

2) по относительным оценкам рангов

которые образуют матрицу:

 

. (6.32)

 

Эта матрица обладает свойствами, аналогичными свойствам матрицы (6.3), т.е.:

а) элементы ее главной диагонали равны единице: ;

б) элементы, которые симметричны относительно главной диагонали, связаны зависимостью: ;

в) она транзитивна, т. е , поскольку .

Напомним, что наличие этих свойств приводит к тому, что при известных элементах одной строки матрицы W легко определить элементы всех других строк: если известна k-ая строка, т. е. элементы , то произвольный элемент w_ij определяется соотношением:

 

.

 

Поскольку матрица W может быть интерпретирована как матрица парных сравнений рангов, то для экспертных оценок элементов этой матрицы можно использовать 9-бальную шкалу Саати [6а]: . В нашем случае эта шкала формируется так:

1 – при отсутствии преимущества R_i над R_j;

3 – при слабом преимуществе R_i над R_j;

5 – при существенном преимуществе R_i над R_j.;

7 – при явном преимуществе R_i над R_j;

9 – при абсолютном преимуществе R_i над R_j;

2, 4, 6, 8 – промежуточные сравнительные оценки.

Таким образом, с помощью полученных формул (6.31) экспертные знания о рангах элементов или их парные сравнения преобразуются в функции принадлежности нечеткого терма. Порядок использования полученных соотношений может быть представлен с помощью следующего алгоритма.

Алгоритм построения функции принадлежности.

Для реализации предложенного метода необходимо:

1. Задать лингвистическую переменную x_k набором ее возможных значений (числовых – если x_k выражается в количественной форме, или номинальных, если x_k имеет качественный, дискретный характер) ; по сути, этим определяется универсальное множество:

 

,

 

на котором задается переменная x_k.

2. Задать совокупность нечетких термов b_jk. Заметим, что для каждой k-ой переменной число таких термов совпадает с числом возможных вариантов B_j второго игрока. По-видимому, и имена этих термов могут совпадать с именами данных вариантов.

3. Для каждого терма b_jk сформировать матрицу (6.32).

4. Используя формулы (6.31), вычислить значения функций принадлежности для каждого терма. Нормирование найденных значений осуществляется путем деления на наибольшие степени принадлежности.

Возвращаемый результат – набор степеней принадлежности

 

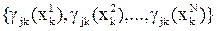, , (6.33)

 

позволяющих определить степень уверенности, что при наблюдаемом векторе признаков Х ^* игроком 2 выбран j-й план игры B_j .

Это делается следующим образом: пусть признак x_k принимает какое-то конкретное значение x_k* = x_k^t. Тогда, на основании (6.33) находим, например, для стратегии B₁ значение γ_1k* = γ_1k^t. Аналогичные значения находим для всех других признаков. Искомая степень уверенности γ₁ находится как

. (6.34)

Отметим, что изложенный метод, как и метод Саати [6а], использует матрицу парных сравнений элементов универсального множества. Но в отличие от метода Саати, он не требует нахождения собственного вектора матрицы, т. е. освобождает исследователя от трудоемких процедур решения характеристических уравнений.

Укажем далее, что для переменных х, имеющих количественную природу, метод допускает дальнейшее расширение, именно, переходом от найденного набора числовых значений γ_jk (х^t_k), t = к некоторой функции γ_jk(х). Такой переход можно осуществить с использованием ряда типовых кривых функций принадлежности (см. Приложение А).

Дальнейшее решение для рассматриваемой модели совпадает с изложенным в предыдущем параграфе.

П р и м е р 6.4. Пусть переменная x определена на 5 уровнях, при этом матрица парных сравнений (6.32) имеет вид

 

W = .

Используя формулы (6.31), получаем:

γ¹ = 1/15,

γ² = 3/15,

γ³ = 5/15,

γ⁴ = 4/15,

γ⁴ = 2/15.

Графически данные значения отображены на рис. 6.2.

Степени принадлежности, γ^t

Уровни, t

Рис. 6.2. Графическое отображение значений γ^t к примеру 6.4

 

П.3. М етодика конструирования и использования нечетких

Игровых моделей

В свете изложенного, методика построения и использования нечетких игровых моделей (для выработки оптимальных в определенном смысле решений) включает в себя следующие процедуры (методика соответствует игре с разнотипными критериями, при отсутствии коалиции и при возможном проведении однократного изучающего эксперимента):

1) определение и подготовка начальных условий;

2) предварительная обработка данных;

3) нахождение решения игры.

Первая процедура предполагает реализацию следующих этапов.

1. С использованием знаний экспертов – специалистов в предметной области принятия решения – определение возможных вариантов {B_j}, , действий игрока 2 ("противника").

2. С использованием знаний лиц, принимающих решения (ЛПР) и экспертов задание допустимых стратегий {A_i}, , игрока 1.

3. Задание набора критериев {J_q}, , определенных в количественной или в качественной форме, определяющих цель принятия решения (задается ЛПР).

4. Выяснение возможностей проведения изучающего эксперимента. При его возможности – переход к этапу 7.

5. Формирование экспертным путем значений {γ_j} – степеней уверенности, что игрок 2 выберет ту или иную стратегию.

6. Формирование списка признаков {x_k}, отражающих результаты эксперимента; задание их значений и определение наборов степеней принадлежности , .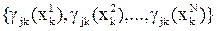

7. Окончание первой процедуры.

Вторая процедура включает в себя следующие этапы.

1. При отсутствии эксперимента – формирование модифицированной матрицы выигрышей вида табл. 6.1. Переход к этапу 3 процедуры.

2. При возможности проведении однократного эксперимента – его проведение, фиксация вектора значений признаков X* и нахождение степеней уверенности {γ_j(X *)}. Формирование модифицированной матрицы выигрышей вида табл. 6.1.

3. Окончание процедуры.

Третья процедура состоит из следующих этапов.

1. Нахождение, в соответствии с вышеприведенными соотношениями, наилучшей альтернативы. Если такая альтернатива – одна, то переход к этапу 3.

2. В случае нескольких наилучших равнозначных альтернатива – выбор одной по ранее приведенным правилам.

3. Окончание процедуры. Выдача ЛПР рекомендаций по оптимальной стратегии.

Отметим, что, вообще говоря, возможны и другие варианты методики (например, в случае чисто количественных критериев и т.п.).

 

Проверочные вопросы

1. Основные понятия теории игр.

2. Какие основные критерии для выбора наилучшей стратегии применяются в матричных играх с природой?

3. Как определяется верхняя и нижняя границы матричной игры?

4. теорема Неймана для матричных игр.

5. Как свести матричную игру к задаче линейного программирования?

6. Итерационный метод решения матричных игр.

7. Основные понятия позиционных игр.

8. Как нормализовать позиционную игру?

9. Позиционные игры со случайным фактором.

10. Понятие равновесной ситуации в биматричных играх.

11. Множество Парето и его приложение к решению биматричных игр.

12. Приведите примеры биматричных игр 2´2.

13. Какая функция называется характеристической?

14. Понятие дележа в кооперативных играх.

15. Как осуществляется дележ с использованием принципа недоминируемых дележей?

16. Арбитражная схема кооперативной игры.

17. Вектор Шепли и его свойства.

18. Кооперативные игры с угрозами.

19. Дайте математическую формулировку многокритериальной модели с разнотипичными критериями.

20. Многокритериальная модель с количественными критериями.

21. Нечеткая игровая модель с единичным экспериментом.

22. Изложите методику конструирования и использования нечетких игровых моделей.

⇐ Предыдущая12345678

Поделиться:

Воспользуйтесь поиском по сайту: