П.3. Позиционные игры со случайным фактором

На практике исход позиционной игры довольно часто зависит не только от действий игроков, но и от случайного фактора (природы). Вмешательство его в игру может быть самым разнообразным. Рассмотрим несколько типичных случаев.

1. Пусть договоренности между игроками об очередности ходов нет. Кто из игроков сделает первый ход, решает случай. В этой ситуации вводится дополнительный игрок О (природа). В парной игре игрок О имеет две стратегии:

О₁ – первым делает ход игрок А;

О₂ – первым делает ход игрок В.

При этом дерево игры разбивается на две части. При решении необходимо нормализовать каждую из частей отдельно. Элементы же общей матрицы будут представлять собой математическое ожидание соответствующих элементов двух матриц.

П р и м е р 3.3. Игрок А и игрок В делают каждый по ходу, выбирая одно из чисел 1 или 2. Очередность ходов не установлена.

Если первый ход делает игрок А, то функция выплат имеет вид:

v_А(1, 1) = 1; v_А(1, 2) = 2;

v_А(2, 1) = 2; v_А(2, 2) = 1.

Если первый ход делает игрок В, то функция выплат следующая:

v_В(1, 1) = - 1; v_В(1, 2) = 0;

v_В(2, 1) = 1; v_В(2, 2) = - 1.

Игрок, делающий ход вторым, не знает, какую стратегию выбрал его противник. Известно, что игроку А удается сделать ход первому с вероятностью р = 0,6.

Необходимо нормализовать данную игру.

Решение. Составим дерево данной игры, вводя дополнительного игрока О (см. рис. 3.3).

1 2 2 1 -1 1 0 -1   1 2 1 2 1 2 1 2   В В А А 2 1 1 2 А В 0,6 0,4 О

Рис. 3.3.

Нормализуем каждую из ветвей дерева отдельно, получим

А = 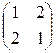, В = .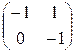

Общую матрицу М найдем следующим образом:

М = 0,6 × А + 0,4 × В = 0,6 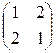+ 0,4 = .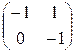

Далее решение данной позиционной игры можно провести симплексным или итерационным методом. 5

2. Пусть теперь природа в позиционной игре выступает в качестве одного из противников. В данном случае для выбора оптимальной стратегии лицу, принимающему решение, желательно иметь следующую информацию:

1) множество вариантов решений для лица, принимающего решения;

2) множество возможных состояний природы и их вероятности;

3) функцию выигрышей при различных вариантах решений и состояний природы.

Рассмотрим конкретный пример.

П р и м е р 3.4. Компания планирует принять участие в тендере на получение некоторого госзаказа. Тендер проводится закрытым способом. По оценкам компании участие в тендере обойдется в 5000 у.е., а выполнение заказа в 45000 у.е. Из опыта предыдущих тендеров известно, что с вероятностью 0,2 конкуренции вообще не будет. Кроме того, известно, что цена подобного товара имеет следующие условные вероятности.

Таблица 3.1.

Цена тендера (у.е.)	Условная вероятность
Менее 65000	0,2
От 65000 до 70000	0,4
От 70000 до 75000	0,3
Более 75000	0,1

 

Необходимо принять решение, участвовать ли в аукционе, и если участвовать, то с какой ценой. Необходимо выбрать стратегию, максимизирующую ожидаемую прибыль.

Решение. Компания должна принять последовательно два решения:

1) участвовать или не участвовать в аукционе;

2) с какой ценой участвовать в аукционе (65000 у.е., 70000 у.е., 75000 у.е.).

После принятия этих решений компании предстоит ждать, как разрешатся неопределенности, т.е. предоставить действовать природе.

Поскольку известно распределение вероятностей, с которыми природа принимает то или иное состояние, логично в качестве критерия оптимальности использовать математическое ожидание выигрыша. Причем, если компания участвует в тендере с ценой М и проходит по цене, то ее ожидаемая прибыль составит (М – 50000) у.е. (50000 = 45000 (стоимость заказа) + 5000 (цена участия в тендере)).

Соответствующее дерево игры приведено на рисунке 3.4.

15000 - 5000 2000 - 5000 25000 - 5000 0,64 0,16 0,48 0,32 0,08 0,72 выигран ли выигран ли выигран ли 0,8 тренд? 0,2 0,4 тренд? тренд? 0,9 0,6 0,1 нет да нет да нет да 15000 20000 25000 0,2 О 0,2 О 0,2 О есть ли есть ли конку- 0,8 есть ли кон- 0,2 конку- 0,8 0,2 ренты? да нет куренты? да ренты? нет 0,2 нет да 0,8 О О О 65000 70000 75000 какую назначить цену? компания 0 участвовать да в тендере? нет   компания

Рис. 3.4.

Дадим пояснение к рисунку 3.4. В данном случае каждой конечной вершине (треугольнику) приписывается два значения. Первое – значение выигрыша, соответствующее данному сценарию развития, второе – это вероятность прихода в данную вершину. Поскольку вероятности, соответствующие ветвям, исходящим из вершин вероятностей, образуют полную группу, то сумма вероятностей по всем ветвям, исходящим из одной вершины, равна 1.

Процедура принятия оптимального решения производится методом обратного хода следующим образом.

1. Для каждой вероятностной вершины (круга) вычисляем математическое ожидание выигрыша по всем альтернативам, исходящим из данной вершины.

а) Для цены тендера 65000 у.е.

Рассчитаем математическое ожидание выигрыша для последней вершины ветви:

v₁ = 0,8 × 15000 + 0,2 × (-5000) = 11000 у.е.

Рассчитаем математическое ожидание для следующей вершины.

= 11000 × 0,8 + 15000 × 0,2 = 11800 у.е.

б) Для цены тендера 70000 у.е.

v₂ = 0,4 × 20000 + 0,6 × (-5000) = 5000 у.е.

= 5000 × 0,8 + 20000 × 0,2 = 9400 у.е.

в) Для цены тендера 75000 у.е.

v₃ = 0,1 × 25000 + 0,9 × (-5000) = - 2000 у.е.

= (-2000) × 0,8 + 25000 × 0,2 = 3400 у.е.

2. Из полученных математических ожиданий выигрыша выбирается максимальное.

max{11800; 9400; 3400} = 11800 у.е.

Отметим, что неучастие в тендере не принесет никакой прибыли (v =0).

Следовательно, компании можно посоветовать принять участие в тендере с ценой 65000 у.е. 5

Заметим, что в более сложных ситуациях принятие решений чередуется с разрешением неопределенностей, причем решения, принятые на очередном шаге, порождают свое множество неопределенностей. При этом деревья игры оказываются достаточно большими и не поддаются обработке вручную. Существует специальное программное средство – Precision Tree, которое является расширением MS Excel, предназначенное для работы с деревьями позиционных игр.

 

⇐ Предыдущая12345678Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: