 |
П.1. Характеристическая функция
|
|
|
|
В реальных ситуациях нередки случаи, когда в конфликтной ситуации участвует более двух игроков. Пусть N = {1, 2, …, n} множество игроков. Обозначим xi – стратегию i-го игрока, Xi – множество стратегий i-го игрока, vi(x1, x2, …, xn) – функцию выигрыша i-го игрока в зависимости от выбранных стратегий x1, x2, …, xn.
Предположим, что часть игроков объединяются в условиях игры в коалиции для борьбы в общих интересах. Обозначим коалицию через К (К Ì N). Объединение игроков в коалицию означает, что они начинают действовать как один игрок. Назовем его игроком А. Множество стратегий игрока А – всевозможные комбинации стратегий игроков из коалиции К. Общность интересов игроков из К означает, что выигрыш игрока А будет складываться из выигрышей игроков из К:
 . (5.1)
. (5.1)
Один из основных вопросов теории кооперативных игр, какой наибольший гарантированный выигрыш может получить игрок А. Очевидно, что ответ на этот вопрос будет зависеть не только от поведения игроков внутри коалиции, но и от того, что предпримут игроки, не вошедшие в коалицию. Обозначим множество таких игроков через J (J = N\K). В худшем для коалиции К случае игроки из множества J могут объединиться в некоторого коллективного игрока В с интересами диаметрально противоположными игроку А. Тогда игра переходит в парную антагонистическую игру, множество ситуаций в которой формально совпадает с множеством ситуаций в исходной игре n лиц.
Заметим, что полученная антагонистическая игра является не более чем «плодом воображения» игроков, входящих в коалицию К. Функции выигрыша, а значит интересы игроков, не вошедших в коалицию, не участвуют в описанной антагонистической игре. Единственное, что интересует игроков К – это в какой мере игроки множества J могут ей навредить, если они того пожелают.
|
|
|
Теперь вернемся к вопросу о том, какую максимально возможную гарантированную прибыль может получить коалиция К. Поскольку игра n лиц была сведена к антагонистической парной игре, напрашивается вывод о том, что можно для ответа на поставленный вопрос воспользоваться принципом максимина. Используя этот принцип, коалиция может прогнозировать игру, не учитывая действия оставшихся игроков. Можно приписать каждой коалиции ее максиминный выигрыш, который, в свою очередь, будет зависеть от состава коалиции, то есть, будет являться функцией от коалиции К. Эта функция называется характеристической функцией.
Определение 5.1. Функцию Ф(К) называют характеристической функцией для игры n лиц, если для любого подмножества К множества всех игроков N (K Ì N) Ф(К) – максимальный суммарный гарантированный выигрыш игроков К при условии их оптимальных совместных действий, т.е.
 . (5.2)
. (5.2)
Характеристическая функция обладает следующими свойствами.
1. Персональность. Для любой игры Ф(Æ) = 0.
Данное свойство означает, что выигрыш принадлежит только игрокам.
2. Супераддитивность. Пусть в игре n лиц образовано две коалиции К и L, причем K Ç L = Æ, тогда
Ф(К È L) ³ Ф(К) + Ф(L).
Свойство супераддитивности означает, что, если игроки из коалиций К и L будут сотрудничать, то коалиция К получит выигрыш не меньше, чем в случае вражды. То же самое можно сказать и о выигрыше коалиции L.
Рассмотрим простой пример.
П р и м е р 5.1. Землевладелец (назовем его игроком А) хочет продать участок, который он оценивает в 100000 у.е. Ему предлагают услуги два дилера (игроки В и С). Игрок В может, разбив данный участок на более мелкие участки, довести стоимость до 200000 у.е. Игрок С может также провести разбиение участка, плюс обустроить его. Тогда стоимость участка возрастет до 300000 у.е. Найти характеристическую функцию игры.
|
|
|
Решение. Для того, чтобы определить характеристическую функцию игры нужно перебрать все возможные коалиции трех игроков и определить их максимальные гарантированные выигрыши.
Ф(А) = 100000,
Ф(В) = Ф(С) = 0,
Ф(А È В) = 200000,
Ф(А È С) = 300000,
Ф(А È В È С) = 300000. 5
П.2. Дележ
Прежде, чем сформировать коалицию, игроки должны:
1) разработать общую стратегию, которая позволила бы получить максимальную прибыль;
2) договориться о дележе прибыли.
Очевидно, что коалиция будет устойчива, если каждый игрок в ней будет знать, что совместные действия принесут ему выигрыш, по крайней мере не меньший, чем тот, который он сможет получить, действуя самостоятельно.
Пусть V = V(v1, v2, …, vn) – вектор выигрышей, где vi – выигрыш i-го игрока в коалиции.
Определение 5.2. Если вектор V удовлетворяет условиям:
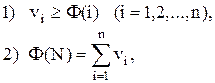 (5.2)
(5.2)
то он называется дележом.
Первое условие (5.2) означает, что выигрыш каждого игрока vi
(i = 1, 2, …, n) должен быть не меньше того количества, которое он может обеспечить себе самостоятельно (индивидуальная рациональность).
Второе условие (5.2) гарантирует, что сумма индивидуальных выигрышей не должна быть меньше того, что может обеспечить себе коалиция в целом.
Очевидно, что для одной и той же игры может существовать достаточно много дележей. Выбрать из дележей лучший с той или иной точки зрения – одна из основных задач теории кооперативных игр. Существует достаточно много критериев выбора дележа. Приведем некоторые из них.
|
|
|


