|
П.3. Оптимальность по Парето
|
|
|
|
Оптимальность по Парето больше, чем равновесные ситуации, уделяет внимания выгодности той или иной ситуации.
Введем понятие множества Парето, причем ограничимся только двумерным случаем. Известно, что все точки некоторого множества W можно разбить на два класса.
1) Точка множества называется внутренней, если все сколь угодно близкие к ней точки принадлежат множеству W (см. рис. 4.1 точка М0).
2) Точка множества называется граничной, если в любой сколь угодно малой ее окрестности есть точки как принадлежащие множеству W, так и не принадлежащие (см. рис. 4.1 точка М1).
 Y
D Y
D
     M1
W M1
W
 C C
   M3
M0 M3
M0
  B B
  M2 M2
 A
O X A
O X
|
Рис. 4.1.
Пусть М произвольная точка множества W. Поставим задачу переместить точку М таким образом, чтобы увеличить обе ее координаты. При этом точка М должна оставаться в области W.
Если точка М является внутренней, то такая задача безусловно выполнима. Если точка М граничная, то ситуация становится сложнее. Здесь возможны три случая:
1) можно увеличить одновременно обе координаты (см. точку М2 на участке границы АВ);
2) можно увеличить только одну, при этом другая остается неизменной (см. точку М3 на участке границы ВС);
3) при увеличении одной координаты другая координата уменьшается или при перемещении точки уменьшаются обе координаты (см. точку М1 на участке границы CD).
Множество граничных точек, для которых справедлив третий случай, называется множеством Парето или границей Парето.
Рассмотрим на плоскости хОу множество w (см. рис. 4.2), которое является областью определения функций:
Ф = Ф(х, у) и Y = Y(х, у).
 Y Y
 w
w
 O X
O X
|
Рис. 4.2.
Перейдем на множестве w точки (хФ, уФ) и (хY, уY), в которых функции Ф(х, у) и Y(х, у) достигают максимума соответственно. Рассмотрим двумерную область W, образованную множеством значений функций Ф(х, у) и
Y(х, у) (см. рис. 4.3).
|
|
|
 Ф
Фmax точка утопии Ф
Фmax точка утопии
   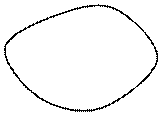
W
O Ymax Y
|
Рис. 4.3.
Возможен случай, когда точка с координатами (Ymax, Фmax) не принадлежит множеству W. Обычно точка (Ymax, Фmax) называется точкой утопии.
Возвращаясь к биматричным играм, заметим, что множество W можно интерпретировать как множество возможных средних выигрышей игроков А и В. В случае, когда точка утопии принадлежит указанному множеству, конфликт исчерпан. Оба игрока к взаимному удовольствию получают максимальные выигрыши. Если точка утопии не принадлежит множеству W, то компромиссное решение можно найти, используя множество Парето.
Общий алгоритм такого поиска таков:
1) строится множество возможных выигрышей W;
2) находится точка утопии (vA max, vB max);
3) определяется множество Парето;
4) находится точка множества Парето, ближайшая к точке утопии.
Надо сказать, что для достаточно больших платежных матриц биматричной игры поиск оптимальных стратегий с точки зрения равновесных ситуаций и с точки зрения оптимальности по Парето является сложной задачей. Поэтому в дальнейшем ограничимся случаем, который не только достаточно прост для исследования, но и допускает наглядную геометрическую интерпретацию. Будем рассматривать биматричные игры 2 ´ 2.
П.4. Биматричные игры 2 ´ 2
Вначале рассмотрим два классических примера биматричных игр
(см. [5]).
П р и м е р 4.1 (борьба за рынки). Пусть небольшая фирма (игрок А) намерена сбыть партию товара на одном из двух рынков, которые контролируются более крупной фирмой (игрок В). Для этого фирма А готова предпринять на одном из рынков соответствующие приготовления (например, развернуть рекламную компанию). Фирма В может воспрепятствовать этому (разумеется, в рамках закона). Не встречая противодействия на рынке, фирма А захватывает его; при наличии препятствия – терпит поражение.
|
|
|
Будем считать, что проникновение фирмы А на первый рынок более выгодно, чем на второй, но зато поражение при попытке освоиться на первом рынке может полностью разорить фирму А и избавить фирму В от конкурента.
Победа на втором рынке фирме А принесет меньший выигрыш, но зато при поражении потери будут не столь значительны.
Таким образом, у игрока А две стратегии:
А1 – выбор первого рынка;
А2 – выбор второго рынка.
Такие же стратегии и у игрока В:
В1 – выбор первого рынка;
В2 – выбор второго рынка.
Для того чтобы составить платежные матрицы игроков, нужны количественные показатели, которые мы приводим в условных единицах:
 ,
,  .5
.5
П р и м е р 4.2 (заключение договора). Два партнера договариваются о совместном проведении одного или двух действий (1) и (2), каждое из которых требует их совместного участия. В случае осуществления первого из этих двух действий выигрыш первого партнера (игрока А) будет вдвое выше выигрыша второго партнера (игрока В). Напротив, в случае осуществления второго действия выигрыш игрока А будет вдвое меньше выигрыша игрока В. Если партнеры выполняют различные действия, то выигрыш каждого из них будет равен нулю. 5
Читатель, видимо, уже почувствовал, что, несмотря на то, что оба примера относятся к биматричным играм, смысл их разный. Если в «борьбе за рынки» слышится такое же «бряцанье оружием», как и в антагонистических играх, то при «заключении договора» сложно представить игроков как противников.
Игры, аналогичные борьбе за рынки, относятся к почти антагонистическим играм.
Определение 4.2. Почти антагонистическими играми называются биматричные игры с матрицами выигрыша  ,
,  , для которых из условия aij < akm следует соответственно bij ³ bkm.
, для которых из условия aij < akm следует соответственно bij ³ bkm.
Почти антагонистические игры поддаются простому и содержательному анализу.
Так как в примере 4.1 a11 < a12 и b11 > b12, a11 < a21 и b11 > b21 и т.д., то биматричная игра «борьба за рынки» относится к почти антагонистическим играм.
Исследуем данную игру методом равновесных ситуаций. Для этого воспользуемся одним конструктивным утверждением для биматричной игры 2 ´ 2. Предварительно введем следующие обозначения. Пусть р – вероятность, с которой игрок А выбирает стратегию А1, q – вероятность, с которой игрок В выбирает стратегию В1.
|
|
|
Теорема 4.2. Выполнение неравенств
vА(p, q*) £ vА(p*, q*),
vB(p*, q) £ vB(p*, q*)
равносильно выполнению неравенств
vА(0, q*) £ vА(p*, q*), vB(p*, 0) £ vB(p*, q*), (4.1)
vА(1, q*) £ vА(p*, q*), vB(p*, 1) £ vB(p*, q*).
Неравенства (4.1) позволяют провести поиск равновесной ситуации.
Пусть
 ,
,  .
.
Запишем математические ожидания выигрыша игроков А и В.
vA(p, q) = a11 p q + а21 (1 – p) q + а12 p (1 – q) + а22 (1 – p) (1 – q) =
= (a11 – а12 – а21 + а22) p q + (a12 – а22) p + (a21 – а22) q + a22, (4.2)
vВ(p, q) = b11 p q + b21 (1 – p) q + b12 p (1 – q) + b22 (1 – p) (1 – q) =
= (b11 – b12 – b21 + b22) p q + (b12 – b22) p + (b21 – b22) q + b22. (4.3)
Рассмотрим формулу (4.2), если р = 1. Получим:
vA(1, p) = (a11 – а12 – а21 + а22) q + a12 + (a21 – а22) q,
Для р = 0 получим:
vА(0, q) = (а21 – а22) q + а22.
Если р и q определяют равновесные ситуации, то
vA(p,q) – vA(1,q) ³ 0,
vA(p,q) – vA(0,q) ³ 0.
или
(a11 – а12 – а21 + а22) p q + (a12 – а22) p – (a11 – а12 – а21 + а22) q + a22 – a12 ³ 0,
(a11 – а12 – а21 + а22) p q + (a12 – а22) p ³ 0.
Если обозначить
С = a11 – а12 – а21 + а22, a = a22 – a12,
то неравенства примут вид
(р – 1) (Сq – a) ³ 0,
р (Сq – a) ³ 0. (4.4)
Проведя аналогичные преобразования для выражения (4.3), получим неравенства:
(q – 1) (D p – b) ³ 0,
q (D p – b) ³ 0, (4.5)
где D = b11 – b12 – b21 + b22, b = b22 – b21.
Таким образом, если пара (p, q)удовлетворяет неравенствам (4.4), (4.5), то она определяет равновесную ситуацию.
П р и м е р 4.1 (продолжение). Найти равновесную ситуацию в биматричной игре «борьба за рынки».
Решение. По платежным матрицам
 ,
, 
найдем необходимые константы.
С = –10 – 2 – 1 – 1 = – 14, a = – 1 – 2 = – 3,
D = 5 + 2 + 1 + 1 = 9, b = 1 + 1 = 2.
Получим неравенства:
 (*)
(*)
 (**)
(**)
Рассмотрим неравенства (*).
Возможны три случая: две чистые стратегии р = 1, р = 0 и смешанная стратегия 0 < p < 1.
1) Пусть р = 1, получим
– 14 q + 3 ³ 0,
 .
.
Изобразим полученный результат графически, используя единичный квадрат. Система  определяет отрезок АВ (см. рис. 4.4).
определяет отрезок АВ (см. рис. 4.4).
2) Пусть р = 0, тогда
– 14 q + 3 £ 0,
 .
.
Система  определяет отрезок CD на рисунке 4.4.
определяет отрезок CD на рисунке 4.4.
2) Пусть 0 <р < 1, тогда

Полученная система совместна в том и только том случае, если  .
.
|
|
|
Система  определяет открытый интервал ВC (рис. 4.4).
определяет открытый интервал ВC (рис. 4.4).
 q q
       1 1
 D D

O 1 A p
|
Рис. 4.4.
Проведем аналогичные рассуждения для системы (**). Получим три множества точек, определяемых системами
1) 
2) 
3) 
На рисунке 4.5 изображены множества точек, удовлетворяющие системам 1, 2, 3 (отрезки А*В*, С*О, В*С* соответственно).
 q В* А* q В* А*
 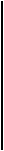       1 1


O 2/9 1 p
|
Рис. 4.5.
Поскольку равновесная ситуация должна устраивать обоих игроков, то точками равновесия будут точки пересечения ломаных ABCD и А*В*С*О. Рисунок 4.6 – объединение рисунков 4.4 и 4.5. В данном случае получена единственная равновесная точка М( ;
;  ).
).
 q q
         1 1


O 2/9 1 p
|
Рис. 4.6.
Получаем:
р =  , q =
, q =  ,
,
vA =  .
.
vВ =  .
.
Таким образом, маленькая фирма, нападая на большую, должна знать, что, скорее всего, окажется в проигрыше (vA < 0). Причем большее внимание следует уделять второму рынку, пусть даже он менее выгоден (р1 = р =  , р2 = 1 – р =
, р2 = 1 – р =  ).
).
Крупная фирма, скорее всего, победит (vB > 0). Однако ей следует также приглядывать за вторым рынком (q1 = q =  , q2 = 1 – q =
, q2 = 1 – q =  ).5
).5
Кстати, вспоминая историю войн, можно заметить, что крупной стране – агрессору труднее всего справиться не с регулярными войсками более слабого противника, а с партизанским движением. Случалось, что более слабый противник выигрывал войну, избегая крупных сражений и сосредотачиваясь на партизанских атаках второстепенных объектов противника.
Заканчивая анализ почти антагонистических игр, заметим, что решение таких биматричных игр можно провести с использованием теории матричных игр. Для этого надо решить две матричные игры по матрицам А и В. При этом по матрице А можно определить оптимальную стратегию игрока В и наоборот, т.е. каждый из игроков по своей матрице может определить оптимальную стратегию противника, но не свою собственную.
Перейдем теперь к примеру «заключение договора». Данная игра не является почти антагонистической, поэтому ее решение даже в такой простейшей постановке оказывается весьма непростой задачей. Попробуем использовать метод равновесных ситуаций.
П р и м е р 4.2 (продолжение). Найти равновесные ситуации в биматричной игре, заданной матрицами
 ,
,  .
.
Решение. Проведем необходимые вычисления:
С = 2 – 0 – 0 + 1 = 3, a = 1 – 0 = 1.
D = 1 – 0 – 0 + 2 = 3, b = 2 – 0 = 2.
Получим неравенства:
 (*)
(*)
 (**)
(**)
Рассмотрим, как и в примере 4.1, следующие ситуации
р = 1, р = 0, 0 £ р £ 1 и q = 1, q = 0, 0 < q < 1.
Получим
1. р = 1,  , и 1. q = 1,
, и 1. q = 1,  ,
,
2. р = 0,  , 2. q = 0,
, 2. q = 0,  ,
,
3. 0 < p < 1, 0 < q < 1, 3. 0 < q < 1, 0 < p < 1.
Геометрически полученный результат представлен на рисунке 4.7.
 q q
          1 1


O 2/3 1 p |
Рис. 4.7.
Таким образом, в данной игре имеется три равновесных ситуации. Две ситуации соответствуют чистым стратегиям игроков, одна – смешанным.
1. р = 0, q = 0.
vA(0, 0) = 1, vВ(0, 0) = 2.
2. р = 1, q = 1.
vA(1, 1) = 2, vВ(1, 1) = 1.
3.  ,
,  .
.
vA =  , vВ =
, vВ =  .
.
Решение данной биматричной игры не является однозначным. Первых две равновесных ситуации призывают одного из игроков уступить и позволить получить другому максимальный выигрыш. Третья стратегия советует «лобовое столкновение». При этом средние выигрыши сторон оказываются равными, что, в принципе, справедливо. Однако, в последнем случае выигрыш vA = vВ = 2/3 меньше того, что мог бы получить уступивший игрок, если дело решилось бы миром. Что выбрать? 5
Попробуем использовать метод оптимальности по Парето.
П р и м е р 4.2 (продолжение). Найти оптимальные стратегии игроков, используя метод оптимальности по Парето.
Решение. Математические ожидания выигрышей игроков А и В представляют собой функции от переменных р и q.
vA = 2 × p × q + 1 (1 – p) (1 – q),
vB = 1 × p × q + 2 (1 – p) (1 – q),
Область определения функций vA(р, q) и vВ(р, q) представляет собой единичный квадрат АВСО (рис. 4.8). Область значений функций vA и vВ в общем случае образует фигуру, изображенную на рисунке 4.9.
 q q
      1 1
 А В А В

O 1 p
|
Рис. 4.8.
 y
O* y
O*
     2 точка утопии 2 точка утопии
  1 M B* 1 M B*
   ¾ ¾
O ¾ 1 2 x |
рис. 4.9.
Точка М(2, 2) является точкой утопии. Множество Парето представляет собой две точки О*(1, 2) и В*(2, 1). Расстояние от точки утопии до точек О* и В* одинаковые.
Заметим, что ситуация, когда игроки использовали смешанные стратегии, в данном методе не рассматривалась. Следовательно, оптимальными по Парето будут стратегии А1, В1 или А2, В2, выбранные игроками одновременно.
Таким образом, результат, полученный методом оптимальности по Парето, позволяет утверждать, что решить конфликтную ситуацию «заключение договора» можно только объединяя свои усилия. При этом один из игроков получит выигрыш 2 у.е., другой – 1 у.е.
Остается вопрос, кто из игроков уступит? Договориться об этом без определенных допущений будет сложно, т.к. ситуация совершенно симметричная. Один из вариантов такой. Пусть игрок А подыгрывает игроку В, выбирая первую чистую стратегию. После игры общий выигрыш
vA+B = vA + vB = 1 + 2 = 3 у.е. делится поровну. В этом случае каждый игрок получает выигрыш больший, чем, действуя в одиночку. 5
Картина, нарисованная в предыдущем абзаце, достаточно радужна. Смущает одно, как договорятся игроки, если игры, которые мы рассматриваем, бескоалиционные. Напрашивается вывод: бескоалиционные игры исчерпали себя, пора переходить к конфликтным ситуациям, в которых возможно создание коалиций.
|
|
|







 C
C
 3/14 B
3/14 B