Определение энтропии неравновесной системы через статистический вес состояния. III начало термодинамики.

Все тепловые явления являются необрат. По этому необратимость тепловых явлений противоречит обратимости тепловых движений атомов и молекул. Необратимость тепловых явлений носит статистический вероятностный характер. Сост макроскопической сис-мы можно характ-ть двояко

1) сост. Сис-мы заданное набором термодинам-х параметров p,V, T, n- это макросостояние

2) сост. Сис-мы при задании всех координат и всех импульсов составл. сис-му наз микросостоянием

Статистическим весом или термодинамической вероятностью наз. число микросост. соответств. Данному макрососоянию.

Переход сис-мы из неравновесного сост. В равновесное представл. собой переход, кот. Осуществл-ся несравнимо большим числом микросостояний чем обратный переход. По этому необратимость тепловых процессов носит вероятностный характер. Вероятность того, что молекула будет находится в первой части сосуда = ½, 2 молекулы =1/4, 3 – 1/8

Число W характ. данное макросост предтавл собой степень беспорядочности макросост. При равновероятн микросост чаще будут осущ те макросост кот соотв большее число микросост, т.е. кот будут иметь больший статист-ий вес W, что соотв большей неупорядочности сис-мы. Больцман устан связь S и W: . Пусть сис-ма разбита на 2 слабовзоимод подсис-мы , тогда число допуст состояний всей сис-мы равно . Больцман предположил, что энтропия S – есть универс функция сис-мы, т.е. 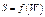, тогда для подсис-м .

В силу аддетивности энтропии имеем .

Решением последнего функционального ур-я явл выражение

;

Покажем, что k – постоянная Больцмана, k= 1,38·10²³ Дж/К, действительно: пусть 1 моль газа расшир в вакууме. Число возможн микросост для одной молекулы прямопропорционально объёму сис-мы. Т.к 1 моль газа содержит -молекул, то число возможн. микросост W пропорционально , тогда S сис-мы будет равна .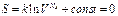

Пусть газ очень медленно расшир в вакуум от объёма до , тогда увелич S будет равно .

С другой стороны изм S одного моля газа при изотерм-м процессе:

.

Славнивая последние выраж, приходим, что k –постоянная Больцмана.

;

16) (ф-ла Больцмана) -Энтропия сис-мы прямопропорциональна логарифму натуралному термодинам-кой вероятности состояний. Процесс явл необратимым, если обратный ему процесс крайне маловероятен. Например: расшир газа в вакуум необрат. По-скольку энтропия имеет вероятностный характер, то такой характер преобр IIНТ. Наиболее вероятным изм-м энтропии явл её увеличение(уточн. 6-ой фор-ки IIНТ).

6) В замкнутой сис-ме наиболее вероятны такие процессы, когда энтропия возростает. Впринципе возожны такие прцессы, при кот энтропия замкнутой сис-мы убывает, но вероятность таких процессов очень мала. Процессы уменьш S в замкнут сис-мах возможны в флуктуациях ( -это случайные отклон наблюд-х физич-х величин от их равновесных статист. Средних) Флуктуации возник за счёт хаотического характера движ молекул. Можно показать, что относ-я флуктуаци обратнопропорц-на корню кв-му из числа молекул N: ∆V/V~1/√N

17) Хаотическому сост сис-мы соотв-т наибольший статист-ий вес W, по этому S= kln W – есть мера хаотичности сис-мы. IIНТ не носит обсолютный характер, в отличии от I и для IIНТ возможны отклонения. Расм. III НТ: «Пусть абсол. , тогда сис-ма как првило будет нах-ся в осн квантово-мех-ом сост-ии, при кот достиг-ся полная упорядоченность сис-мы (квантовый кристалл). Это сост-е осущ-ся в отсутсвие вырождения единственным образом». W=1, тогда , тогда приходим к IIIНТ или тепловой теореме Нернста: « энтропия сис-мы при обсалютном нуле обращается в ноль». Покажем теперь недостижимсть абсол-го нуля температуры.Действительно: пусть абсол-ый ноль темпер-ры достижим, тогда КПД машины и если Т₂=0, то , что противоречит IIНТ( <1).