 |
Смачивание и капиллярные явления
|
|
|
|
Рассм. явления происход. на границе раздела жидк-ти и тв. тела. Опыт показыв., что свободн. пов-ть жидк-ти вблизи стенок сосуда искривл-ся. Искривлённая свободн. пов-ть жидк-ти назыв. мениск. Краевой угол θ это угол отсчит. внутри жидк-ти между касательными к пов-ти жидк-ти и тв. тела.Если θ<90°, то жидк-ть смачив. стенки сосуда.Если θ>0, то жидк-ть не смачив. стенки сосуда.Если жидк-ть смачив. тв. тело, то силы взаимод. между молекулами жидк-ти меньше, чем силы взаимод. между молек. тв. тела(и наоборот).Вода смачив. стекло, а ртуть нет. Найдём давл. над изогнутой пов-тью жидк-ти. Если плёнка огранич. плос-ким контуром, то она стрем-ся сохран. его форму, тогда выпукл. плёнка давит на нижележащ. слои. Рассм. жидк-ть:
Избыточн. давл. равно:
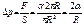(формула Лапласса);
Если форма более сложная:
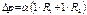
Рассмотрим капиллярн. явлен.Пусть жидк-ть смачив. стенки капилляра. Капилляр – узкая трубка. Добавочное отрицательн. давление приводит к поднятию жидк-ти в капилляре на h. Возникает равновесие, если вес столба жидк-ти уравновешив. добавочн. давление, т.е. ρgh= 
; r=R∙cosθ; h=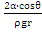 
(высота поднятия жидк-ти в капилляре).Капиллярн. явлен.использ-ся в деревьях, пахотном деле, строит-ве.
Принцип динамич. отопления
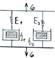Эта идея была предложена Томсоном. При обычн. способе отопления, тепло получаемое в топке от сгор. топлива прямо поступает в отапливаем. помещение. При этом значительн. часть тепла уносится со сгораемыми газами и бесполезно расходуется для нагрева окруж. атмосферы. При динамич. отоплении только часть тепла. получ. от топки затрачив-ся на работу, производим. тепл. машиной. Нагревателем в тепл. машине служит топка, а холодильником– отаплив. помещение. Рабочая тепл. машина использ. для приведения в действие холодильн. машины, включ. между окружающей средой и помещением. Холодильн. машина отбир-т тепло от окруж. среды и передаёт его помещению(работает как обычн. холодильник).Таким образ. помещение получ. тепло и от горячей топки и от холодной окруж. среды.Общее кол-во тепла для помещения может превзойти тепло, получ. только от топки при обычн. способе отопл. Схема динамич. отопления:
|
|
|
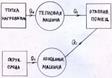Тепло в помещении:Q=Q1+Q2 
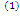. Qн –тепло, получ. от топки. Покажем, что Q>Qн : η тепл.машины равно η= 
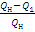=1- 
; =1-η; Q1=(1-η)∙Qн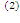 
; ε= 
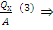A=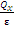 
⇒ Qx=ε∙A 
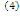. Тепло Q2=Qx+А=εА+А=(ε+1)А 
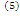;η=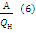 
; А=ηQн 
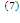. Подставл. (7) в (5): Q2=(1+ε)ηQн ; Q=(1+ε)ηQн+ Q1= (Q1 из (2))=(1+ε)ηQн+(1-η) Qн=(1+εη)Qн > Qн Но по технич. причинам проект не реализован.
Элементы физики полимеров
Полим широко использ. в строит-ве. Полим–высокомолек. соед. в виде пространств., слоистых и линейных структур. Молекулярн. масса полим. может меняться от 5000 до неск. миллионов. Полиэтилен – цепочка молекул этилена (СН2) –СН2–СН2–СН2– Возможно 4 вида конденс. полимеров:кристаллич., жидкие, стеклообразн., высокоэластичн.(каучук).Для реальных полимеров харак-но сочет. св-в упругости и вязкости. В одном случае полим. ведёт себя как упругие тела, а в других как вязкие жидк-ти. Для полим. рассм. механич. модели, представл. собой набор пружин и демферов.Демфера(амортизатор)–жёсткое тело правильной формы, погруж. в вязкую ньютоновскую жидк-ть. Амортизатор подчин-ся з-ну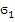 
=η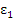 
Пружина подчин-ся з-нк Гука 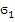=Е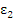 
При последоват. соедин. любых элементов модели действующая сила одинакова во всех элементах, а общ. деформация равна сумме деформ. каждого из элементов. При параллельн. соед. элементов общая деформ. одинакова, а напряжение равно 
напряжений в каждом из элементов.
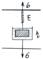Текучесть – величина обратная η. Упруговязкой назыв. полимерн. жидк-ть, кот. проявл. наряду с текучестью и упругость формы(простейшая модель–Максвелла). В этой модели объедин-ся з-н Гука и з-н вязкости. Модель состоит из упругой пружины и вязкого амортизатора, соед. параллельно. Её вид:
|
|
|
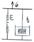Вязкоупругим назыв. упругое тв. тело, имеющее внутрен. трение. Такое тело описывает модель Кельвина-Фойгта. Она состоит из амортизатора и пружины, соедин. параллельно.
Двойная модель Максвелла–2 одинарн. модели, соед. параллельно.Такая модель включает в себя как частн. случай предыдущ. модель.
Если Е2=0,то получ. обычная модель Максвелла. Если η1=∞ и Е2=∞, то получ. модель Кельв.-Фойг. Если η2=∞, то получим модель Зингера.
|
|
|
