 |
Метод термодинамических потенциалов (характеристических функций).
|
|
|
|
Термодинамическим потенциалом наз функция сост из термодинам-х параметров (p,V,S,T). Каждому набору таких параметров соотв. свой потенциал. Изменение потенциала в ходе прцесса опред либо работу в сис-ме либо тепло получ-мое сис-мой. Приращение любого из потенциалов = полному дифф-лу функции, которой он выраж. Полный дифф-л функции f(x,y),будет равен
.
Рассм термод-ий потенциал:
1) Внутр энергия 
. Осн. Термод-е тождество:
,
.
IНТ: 
. Работа сис-мы в адиобатном процессе равна убыли внутр энергии сис-мы.
2) Свободная энергия или энергия Гельмгольца: F=F(T,V)
IНТ: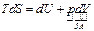 
; 
, если процесс изотерм-ий 
, то 
; 
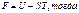при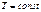 
, 
т.е. работа в изотерм-ом прцессе игрант такую же роль, что и внутр-я энергия в адиобатном.
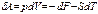
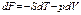
3) Тепловая функция (Н) или энтальпия:
Н=Н(S,p) - Энтальпия
Если процесс изобарный т.е. р=const, тогда IНТ: 
4) Потенциал Гиббса
. Можно показать, что минимум потенц. Гиббса соотв-т равновесию сис-мы при р=const.
Явления переноса. Средняя длина свободного пробега молекул.
ТД система находится в неравновесном состоянии, если его ТД-параметры не имеют определенного значения. Время перехода системы из неравновесного состояния в равновесное – время релаксации. Время релаксации может быть различно, но различны параметры, тогда за время перехода берется наибольшее из времен релаксации системы. Вычисляя среднее число столкновения и среднюю длину свободного пробега молекул. Молекулы, находящиеся в тепловом движении непрерывно сталкиваются между собой. Пусть Li проходимость i молекулы между двумя последующими столкновениями наз. длину свободного пробега.
Средняя длина свободного пробега молекул
Эффективный диаметр молекулы (d) – минимальное расстояние, на которое сближаются при столкновении центры молекул. За 1с молекула проходит в среднем путь равный средней арифметической скорости молекулы. Пусть <z> -- среднее арифметическое число столкновений, испытываемой одной молекулой за 1 секунду, тогда средняя длина свободного пробега молекулы:
|
|
|
Найдем среднее число столкновений z за 1с:
Пусть молекула – шарик с диаметром d и это молекула движется среди неподвижных молекул со скоростью <V>, тогда эта молекула сталкивается со всеми молекулами, центры которых находятся от центра молекул на расстоянии равном или меньшем d, т.е. лежат внутри ломаного центра R=d.
Среднее число столкновений за 1с -- число молекул в объеме ломаного цилиндра, т.е.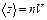 
Объем цилиндра после его выравнивания равно 
Учет движения молекул приводит к увеличению числа столкновений в 
раз.
Средняя длина свободного пробега молекул:
; 
Для воздуха при t=0, p0=1 атм. средняя длина свободного пробега 
, эффективный диаметр 
, среднее число столкновений 
, средняя скорость 
Коэффициент диффузии.
Рассмотрим смесь из двух газов и концентраций.
Диффузия в газе есть направленный перенос молекул при наличии градиента концентрации, перенос происходит из мест большей концентрации в места с меньшей за счет хаотического числа молекул до полного выравнивания газов.
Рассмотрим одномерный случай
Найдем поток молекул 
за время 
через площадку с площадью 
, перпендикулярно оси х и имеет координату х.
В силу хаотичного движения молекул вдоль оси х будет двигаться 1/3 молекул от их общего числа, тогда вдоль положительно направленной оси х будет двигаться 1/6.
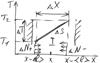
Через площадку слева на право пройдет 1/6 часть всех молекул заключается в цилиндре с длиной <v>t и площадью основания
Концентрация молекул в точке слева от площади , т.к. концентрация молекул меняются только за счет их столкновения.
Диффузионный поток молекул за единицу времени через единицу площади равно 
|
|
|
Преобразуем последнее выражение
З. диффузии Фика: 
Диффузный поток молекул примеси проходит через единицу площади за единицу времени прямопропорционально градиенту концентрации. Знак «минус» указывает, что перенос молекул примеси направлен в сторону убывания концентрации. Коэффициент диффузии (Д) – поток молекул через единицу площади за единицу времени при градиенте концентрации равном (-1).
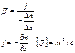
Для воздуха Д=10-5 м2*с
Нелинейные элементы диффузии
Получено уравнение диффузии, т.е. диффузионные уравнения в частных производных описывается процессом концентрации диффузии. Изменение числа молекул в слое х. х+dх, с объемом Sdx будет равно – чило молекул входящих в слой за единицу времени через поверхность S «минус» число молекул примеси, вдящих из слоя через поверхность S за единицу времни. 
В трехмерном случае
|
|
|
