A1.8. Дифракция и гауссовский пучок лучей

 

Дифракция является фундаментальным явлением, связанным с волновой природой распространения света и показывающим ограничение геометрической лучевой оптики. Невозможно изолировать один луч в оптической волне. При выборе маленького отверстия фильтрации света можно отметить его угловое расхождение со "средним" углом θ _D, который увеличивается с уменьшением размера отверстия a_h (Рисунок A1.20):

 

(А1.109)

 

Дифракция может быть объяснена тем, что в соответствии с принципом Гюйгенса каждой точке отверстия испускаются сферические волны, и эти сферические волны совместно интерферируют. Амплитуда дифрагируемой волны в данный момент представляет сумму амплитуд всех этих интерферируемых волн.

Ввод лучей

Маска

Дифракция

Рисунок A1.20.Дифракция волны

Дифракция на ограниченном расстоянии, известная как дифракция Френеля, сложна математически, но дифракция на бесконечном расстоянии (или в фокальной плоскости объектива, создающего «имидж бесконечности»), известная как дифракция Фраунгофера, имеет более простое решение. В данном направлении θ волны интерферируют с соответствующей разностью хода (Рисунок A1.21):

(A1.110)

 

Затем общая амплитуда дифракции A_d в направлении θ

 

(Al.111)

Сферический фазовый фронт

Аd

Маска

Рисунок A1.21. Расчет дифракции Фраунгофера

где A_f – амплитуды пространственно отфильтрованных волн. Следовательно, амплитуда дифракции является преобразованием Фурье пространственно отфильтрованных амплитуд . Отношение соответствует тому факту, что произведение ширины пары преобразований Фурье постоянно.

Этот интерферометрический анализ дифракции можно объяснить простыми аргументами: в направлении угла такого, как , каждая сферическая волна, излучаемая в отверстии фильтрации, имеет соответствующую разность хода λ/2, а затем обе волны интерферируют, взаимно уничтожаясь. Обратите внимание, что дифракция – это явление, неразрывно связанное с длинами волн; таким образом, в среде возникает тот же эффект, но в зависимости от фактических длин волн λ _m =λ/ n.

Поскольку многополевая дифракционная модель является пространственным преобразованием Фурье отфильтрованных амплитуд распределения, особый интерес представляет распределение Гаусса, потому что гауссовскя функция инвариантна к преобразованию Фурье. Особенно такие гауссовские лучи создаются в газовых лазерах. Гауссовские лучи, распространяемые вдоль оси 0 z, имеют узкие части (горловины) с распределением радиальных амплитуд (Рисунок A1.22):

 

(А1.112)

Дальнее поле

W(z)

z

Рисунок A1.22. Гауссовский пучок света

и распределением интенсивности в соответствии с распределением площади амплитуд:

(A1.113)

 

Член w ₀, называемый горловиной, это радиус 1/ e по амплитуде и 1/ e ² по интенсивности (и 2 w ₀ – диаметр у 1/ e ²), следовательно

 

(A1.114)

 

От горловины лучей свет дифрагирует, но сохраняет гауссовское распределение амплитуды:

 

(A1.115)

с

(A1.116)

Эта формула может быть упрощена в двух случаях:

1. примерно постоянна: ;

2. пропорциональна z:

 

(A1.117)

Гауссовские лучи расходятся с полным углом θ _D с интенсивностью 1/e²:

(A1.118)

(A1.119)

и он определяется

(A1.120)

 

как указывалось выше, если учесть, что, около "ширины" апертуры.

В этом последнем случае свет дифрагирует с постоянным углом расхождения, и когда условие выполняется, вполне возможно, что результатом дифракции может быть приближение дифракции Фраунгофера, даже если расстояние остается конечным. Это условие может быть обобщено для любого фильтрующего отверстия и когда , вполне возможно, что наблюдается дифракция Фраунгофера. Эту дифракционную модель часто называют дальним полем (far field).

 

A 1.9. Когеренция

В случае идеальной плоской монохроматической волны, фаза волны дается точкой, которая может быть выведена из фазы любой другой точки:

• фаза это несколько одинаковых точек на одном и том же фронте переноса поперечно к направлению распространения. Это идеальное "поперечное соотношение" называется пространственной когерентностью;

• разность фаз между двумя различными фазовыми фронтами может быть выведена из расстояния d между обоими фазовыми фронтами с . Это идеальное "продольное соотношение" называется временной когерентностью.

На практике этот идеальный случай невозможен, и волна имеет ограниченную когерентность. Полная теории когерентности сложна и предполагает математический аппарат стохастических процессов. Тем не менее, мы будем анализировать проблемы временной когерентности, которые очень важны для интерферометрического волоконно-оптического гироскопа. С другой стороны, волоконный гироскоп использует одномодовый волновод, и пространственная когерентность обеспечивается автоматически, поскольку все точки моды идеально коррелированны по фазе в поперечном направлении.

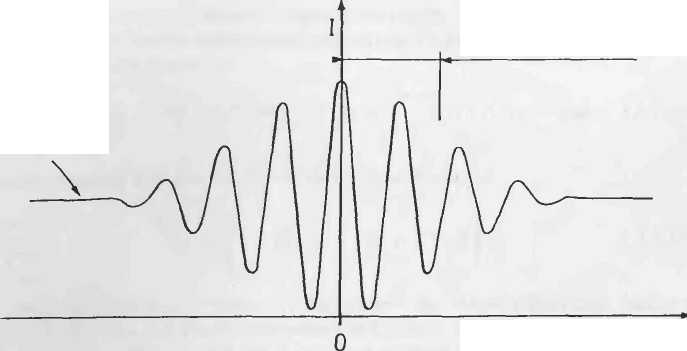
Когда источник посылает в интерферометр широкий спектр излучения, наблюдается хороший интерференционный контраст около нулевой разности хода, и так как эта разность увеличивается (в абсолютном значении), наблюдаемость интерференционных полос уменьшается и, наконец, полностью исчезает (Рисунок A1.23). Когда разность хода длиннее, чем данная длина корреляции, называемая длиной когерентности L_c от источника в оптике, обе интерферируемые волны больше не коррелируют, и разность их хода зависит от времени, которое осредняется по члену в формуле интерференции.

 

Длина когерентности

Потеря контрастности

Разность хода

Рисунок A1.23. Интерференционный сигнал с источником широкого спектра

Другим способом понять феномен является разложение широкого спектра на отдельные длины волн. Каждая длина волны λ _i создает свой собственный интерференционный шаблон с периодом λ _i. Около нулевой разности хода все интерференционные шаблоны совпадают; но как только разность хода увеличивается, их совпадение теряется, потому, что они имеют слегка разные периоды (Рисунок A1.24). Поскольку некоторые длины волн на ярких полосах, а другие из них находятся на темных полосах, в среднем, общая интенсивность становится постоянной и контраст исчезает. Длина когерентности L_c обратно пропорциональна ширине спектра Δλ.

Точный результат может быть получены строго с преобразованием Фурье. Рассмотрим волну с амплитудой A (t), которая изменяется как функция времени t в заданном пространстве. Как мы уже видели, компоненты частот a (f) этих амплитуд A (t) могут быть определены преобразованием Фурье:

(A1.121)

 

и, наоборот, амплитуды волн A (t) является интегральными суммами всех компонентов их частот:

(A1.122)

 

Яркий край

Темный край

Разность хода

Рисунок A1.24. Сигналы интерференции в зависимости от разности хода

 

В целом, частоты компонентов a (f) являются сложными и могут быть написаны с положительными реальными модулями и составляющими фазы :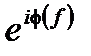

(A1.123)

 

Когда эта волна посылается в интерферометр двумя 50-50 (по интенсивности) пучками, имеется интерференция между волной A (t) с ее самой, но сдвинутой при временной задержке τ, A (t– τ). С учетом того, что свет распространяет в вакууме вдоль обоих путей, временная задержка τ связана с геометрической разностью хода Δ L:

(A1.124)

 

Следуя сохранению энергии, каждый пучок разделителя 50-50 уменьшает интенсивность в 1/2 и амплитуду в . Поэтому после прохождения двух разделителей наблюдается интерференция между и . Интенсивность I интерференционной волны

 

(A1.125)

(A 1.126)

(A1.127)

 

где скобки 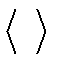обозначают временное усреднение. Член 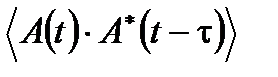пропорционален автокорреляционной функции Г(τ) от функции A (t), определенной в теории обработки сигнала как

 

(A1.128)

 

Затем интенсивность I интерференции пропорциональна

 

(А1.129)

 

Основная автокорреляционная теорема, также называется теоремой Винера-Хинхина, гласит: «если A (t) имеет преобразование Фурье a (f), то его автокорреляционная функция имеет реальное и позитивное преобразование Фурье, равное спектральной плотности мощности ». Поэтому

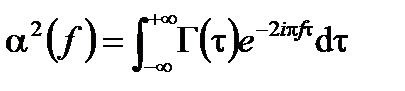(A1.130)

и обратно

(A1.131)

На практике спектральная плотность мощности центрируется около средней частоты , и может быть определена "по центру" спектра (Рисунок A 1.25)

(A 1.132)

Затем

(А1.133)

и

(А1.134)

 

Рисунок A1.25. Интенсивность спектра в зависимости от временной частоты f: (a) фактический спектр α2(f); (b) по центру спектра

 

где – обратное преобразование Фурье по центру интенсивности спектра .

Если спектр симметричен относительно средней частоты , центрирование спектра является даже реальной функцией и ее обратное преобразование Фурье Г _с (τ) также является реальной функцией (т.е. и 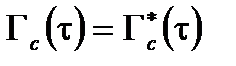). Начиная с

 

(A1.135)

 

где I _in – интенсивности волны на входе. Интенсивность I интерференционной волны

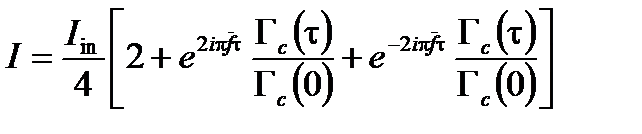(A1.136)

 

И, наконец, возможно определить нормализованную по центру функцию автокорреляции:

(A1.137)

где и . И, наконец

 

(A1.138)

 

С точки зрения пространственных координат существует

 

(A1.139)

 

где разность хода Δ L = c τ и средняя длина волны .

Затем эффект широкого спектра дает наблюдаемость с уменьшением косинусоидальной модуляции интерференционных полос, с уменьшением при возрастании 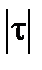(или уменьшением 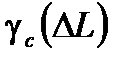при возрастании ). На самом деле получаем наблюдаемость полос интерференции

 

, (A1.140)

 

где называется функцией когерентности источника, нормализованное обратное преобразование Фурье по центру спектра интенсивности (Рисунок A1.26).

Преобразование Фурье

Рисунок А1.26. Центр спектра α2c (f) и функция когерентности γ с (τ) (принимает форму гауссового распределения)

«Полуширина» функции называется временем когерентности τ _с входной волны A (t). Эта «полуширина» определяется классически как среднеквадратичное отклонение (ско) от или от половины ширины «от 1σ»(см. Борн и Вольф):

(A1.141)

 

Когда по центру спектра интенсивность и его нормализованного преобразования Фурье , гауссиана, расчеты являются простыми и дают

 

(A1.142)

так как

(A1.143)

и

(Al 144)

 

Затем время когеренции τ _с это время, обеспечивающее (Рисунок A 1.26)

 

 

Обратите внимание, что полуширина 2σ (т.е. 2τ _с) это полуширина на 1/ e, поскольку

(А1.145)

 

Также можно определить ско полуширины интенсивности спектральной плотности :

(A1.146)

 

В случае когда гауссиан, имеем

 

(A1.147)

и

(A 1.148)

 

Когда и парное преобразование Фурье, произведение их ско полуширин является 1. Поэтому,

(A1.149)

 

Этот результат получен именно для гауссовского спектра, но он по-прежнему приблизительно справедлив и для других фигур спектра.

Длина когеренции L_c определяется

(A 1.150)

и поэтому , где Δλ – ско полуширинный спектра длин волн,

 

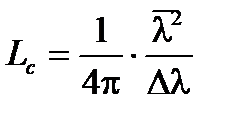(A1.151)

 

Как мы уже видели, время когерентности τ _с и длина когерентности L_c соответствуют максимальной временной или пространственной задержке, которая сохраняет хорошую видимость интерференционных полос:

 

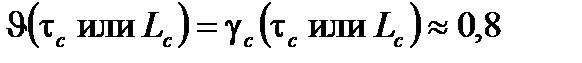(A1.152)

 

Как видно из анализа когерентного шума в волоконном гироскопе, время или длина, выше которой волна теряет свою когерентность, также представляет интерес. Хорошо определять это время "декогерентности" как обратное к полной ширине полумаксимума 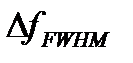спектра (Рисунок A1.26):

 

Затем длина "декогерентности" L_dc

(A1.153)

так как

С переходом назад к простому случаю гауссовских функций установлено, что

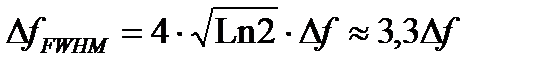(A1.154)

и затем,

 

которое означает, что для τ _dc (или L_dc) контраст был сокращен до 3%.

Время когерентности τ _с полуширинное на lσ и время "декогерентности" определяемое как 1/Δ f_FWHM фактически полуширина от 3σ до 4σ (полуширина в l/ e будучи полуширинными на 2σ).

Эти результаты, полученные именно для гауссовских функций, могут быть приблизительно продлены для любого «колоколообразного» спектра. Тем не менее, решая определенные паразитные эффекты в волоконном гироскопе, необходимо знать точно функцию полной когерентности источника, а не просто его половину ширины.

Очень важным результатом анализа является тот факт, что функция автокорреляция и видимость интерференционных полос зависят от преобразования Фурье спектральной плотности мощности , а не спектральной плотности амплитуды 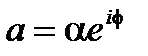. Как обычно указывается, процесс автокорреляция теряет информацию о фазовых спектральных составляющих А (t).

Это означает, что волны с теми же модулями α(f), но различными фазами ф(f) их частотных компонентов, дают ту же видимость интерференционных полос. В частности источник широкого спектра имеет частоты компонентов со случайными фазами, а импульсы амплитудной модуляция имеют частотные компоненты, которые имеют ту же фазу; но оба дают ту же видимость интерференционных полос, если у них есть та же мощность спектра α²(f). Зачастую временнáя когерентность источника широкого спектра объясняется поведением рассматриваемых волновых цугов, равных по продолжительности времени «декогеренции» τ _dc и длиной, равной длине "декогеренции" L_dc. Они на самом деле изображают пульсации с чисто амплитудной модуляцией; но поскольку фаза теряется в автокорреляции, они дают тот же контраст интерференции, что и источник широкого спектра действия. Это позволяет анализировать просто эффект во времени, особенно, когда волновой цуг отправляется в несбалансированный интерферометр, есть два волновых цуга на выходе. Если дисбаланс хода Δ L_op больше, чем волновая последовательность длиной L_dc, две волновых последовательности на выходе не пересекаются и не могут интерферировать (Рисунок A1.27).

Примечание: Эти результаты просты, если спектр симметричен, или даже центризован. Когда нет симметрии, как в случае с широкополосными источниками, используемыми в волоконном гироскопе (суперлюминесцентный диод или источник с редкоземельными легированными волокнами), анализ спектра является более сложным. Центральная спектральная плотность должна быть разложена на четную плотность и остаточную нечетную плотность (Рисунок A1.28):

 

 

Рисунок A1.27. Распространение волновой последовательности импульсов в несбалансированном интерферометре

ввод волнового импульса

не совпадают

 

(A1.155)

 

 

Средняя частота 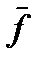излучения определяется как частота, которая минимизирует . Четные компоненты дают преобразование Фурье на четной и реальной автокорреляционной функции , но остаточные нечетные компоненты дают через Фурье преобразование нечетную чисто мнимую функцию автокорреляции . Получаем интерференцию

(Al.156)

 

где и – соответственно нормализованы

Рисунок A1.28. Разложение асимметрического спектра и согласованность соответствующих функций

Несимметрично

Реальная

Мнимая

Четная

Центр силы тяжести

Нечетная

Преобразование Фурье

(А1.157)

(А1.158)

с

(А1.159)

и

 

с тех пор как функцию нечетную

 

По сравнению со случаем симметричного спектра, есть дополнительный термин , который является четной функцией от τ, поскольку это произведение двух нечетных функций: и . Даже с асимметричным спектром интерференция по-прежнему симметрична относительно нуля. Однако, в связи с этим дополнительным термином пересекающая нуль модулированная интерференционная полоса потеряла периодичность косинуса для и так далее. Этот эффект обычно ничтожен в интерферометрическом волоконном гироскопе, который работает на центральных полосах около о нулевой разности фаз, но это возможно, придется учитывать в некоторых схемах стабилизации спектра. Обратите внимание, что этот анализ проводится с частотным спектром, который имеет одинаковую форму, если мы наблюдаем временные частоты или пространственные частоты σ= f / c. На практике часто дается спектр с длиной волны λ, которая обратно пропорциональна частотам λ= l/σ = с / f; и симметричный частотный спектр не дает строго симметричный спектр длин волн (также наоборот, симметричный спектр длин волн не дает строго симметричный частотный спектр), особенно с большой относительной шириной (большой процент) широкополосных источников, желательных для применения в волоконном гироскопе (Рисунок A1.29).

Примечание: Этот анализ дает определение времени когеренции τ _с (и времени декогеренции τ _dс) которое характеризует спектра источника. Наблюдая этот эффект, интерферометр был использован в вакууме, где временная задержка τ связана просто с геометрической разностью хода Δ L между обоими путями интерферометра:

(A1.160)

 

Пространственный эквивалентн временного количества τ _с и τ _dс может быть определен как длина когеренции L_c = с · τ _с и длина декогеренции L_dc = с · τ _dс, которые также характеризуют источник.

Частота

Длина волны

Рисунок A1.29. Проблема спектра симметрии: (а) случай симметрии с категорией пространственных частот σ; (b) связанный асимметрично применительно к категории длины волны λ (обратной от σ)

Теперь, когда свет распространяет в среде, результат более сложен из-за последствий дисперсии. Как мы видели в раздел А1.3, амплитуда A может быть разложена как произведение:

• монохроматической волны с частотой, равной средней частоте , и распространяемой с фазовой скоростью ;

• модулированного термина М, который распространяется с групповой скоростью .

Временно имеем

(A1.161)

 

и, принимая во внимание пространственное распространение, имеем

 

(A1.162)

 

Можно доказать, что автокорреляционная функция М является на самом деле обратным преобразованием Фурье по центру спектра α _c:

 

(A1.163)

 

Возвращаясь назад к концепции волновой последовательности, можно показать, что волновая последовательность синусоидальных волн, модулируемых по амплитуде с огибающей M_wt (t), автокорреляционная функция которой также равна Г _c (t). Амплитуда волновой последовательности

 

(A 1.164)

 

Теперь следующая формула остается в силе, поскольку она была подготовлена только с временной координатой:

 

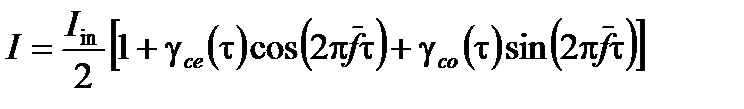(A1.165)

 

Тем не менее, когда свет распространяется в среде, простое соотношение Δ L =с·τ больше не является допустимым. Временная задержка τ уже не соответствует той же пространственной задержке для автокорреляционных составляющих γ _ce и γ _co и для "интерференционных полос" косинуса и синуса. Затем в интерферометре по одной траектории в среде 1 с геометрической длиной пути L ₁ и по другой тректории в среде 2 геометрической длиной пути L ₂ фактические временные задержки в обоих случаях отличаются. Это:

· для автокорреляционных составляющих γ _ce и γ _co, поскольку они являются производными от M (t), которая распространяется с групповой скоростью v_g. Эта задержка называется групповой временной задержкой, обозначается τ _g. Это также время распространения огибающей волновую последовательность.

· для составляющих «интерференционных полос», поскольку они производные от , которые распространяется с фазовой скоростью v. Эта задержка называется фазовой временной задержкой, обозначается τ_ф, с .

Таким образом, в общем случае, интенсивность интерференции

 

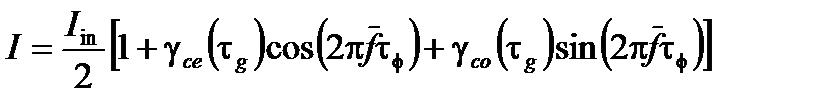(A 1.166)

 

На практике материальная дисперсия дает лишь небольшие различия между τ _g и τ_ф, но интерферометрические измерения очень чувствительны и это может привести к побочным эффектам. Например, в интерферометре Майкельсона эта проблема устраняется дополнительной компенсирующей пластинкой, отменяющей из эффект рассеивания материала и поддерживающая разделение 50-50.

В волокне существуют некоторые случаи, когда τ _g может очень отличаться от τ_ф, как будет показано в приложении 2.

A1.10. Двулучепреломление

Как мы видели, в изотропной линейной диэлектрической среде, производная электрического поля D пропорциональна электрическому полю Е:

 

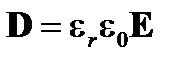(A1.167)

 

Газы, жидкости и аморфные твердые вещества подобные стеклу или кварцу, изотропны, поскольку их структура является случайной, и они не имеют какой-либо преобладающей оси ориентации. И наоборот, кристаллы имеют упорядоченную решетку с преобладанием осей, и их диэлектрическая проницаемость может зависеть ориентации поля. Они имеют три основных ортогональные оси x, y и z. Диэлектрическая проницаемость зависит от основных осей:

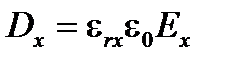
(A1.168)

 

Каждому значению ε _ri соответствует значение показателя преломления при i = x, y или z.

Кристаллы можно разделить на три группы:

• Кристаллы кубических систем, например, как алмаз, в котором n_x = n_y = n_z. Они оптически изотропны и ведут себя как оптически аморфные стекла.

• Однонаправленные кристаллы, которые имеют две обычные оси с n_x = n_y = n ₀ и одну необычную ось с n_z = n_e ≠ n ₀. Разность показателей преломления при двулучепреломлении заключается в Δ n_b = n_e – n ₀. Двулучепреломление считается положительным, когда Δ n_b > 0 (т.е. n_e > n ₀) и отрицательным, когда n_e < n ₀. Необычную z-ось часто называюс С -осью одноосного кристалла.

• Биаксиальные кристаллы, которые имеют различные индексы для каждой оси: n_x ≠ n_y ≠ n_z.

Когда волна линейно поляризована вдоль главной оси, она распространяется с показателем преломления (при i = x, y или z), соответствующим оси электрического поля, поэтому, как мы уже видели, эффект от поля В волны в веществе является обычно незначительным. Например, волна, которая линейно поляризованна вдоль оси x и которая распространяется вдоль y - или z -осей, имеет скорость c / n_x.

Распространение вдоль промежуточных направлений сложнее, но проблемы двулучепреломления, которые мы должны анализировать в волоконной оптике, просты, поскольку они связаны с распространением только вдоль одной основной оси. Главный эффект двулучепреломления заключается в том, чтобы изменить состояние поляризации во время распространения, когда волна не линейно поляризована вдоль основной оси.

Рассмотрим плоскость двулучепреломления с x - и z -осями, параллельными поверхности раздела, и y-осью в направлении распространения (Рисунок A1.30). Входное состояние поляризации при прохождении через плоскость изменяется на выходе. На входе состояние E_in может быть разложено вдоль основных x - и z -осей на плоскости:

 

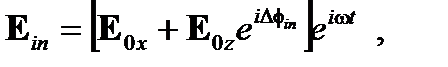(A1.169)

 

Пластинка двойного лучепреломления

Рисунок A1.30. Изменение поляризации вследствие распространения в среде с двулучепреломлением

где 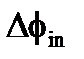– разность фаз между обеими компонентами на входе. Каждый компонент E_{0 x} и E_{0 z} распространяется без изменения поляризации. На выходе состояние поляризации становится

(A1.170)

 

Разность фаз между обеими компонентами на выходе:

 

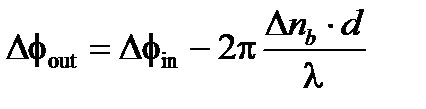(А1.171)

 

где d – толщина пластинки и Δ n_b = n_z – n_x.

Изменение состояния поляризации вдоль распространения через пластину периодическое. Разность фаз увеличивается линейно с толщиной d, и ввод состояния поляризации восстанавливается, когда накопленная разность фаз становится 2π рад. Пространственный период изменения называется пульсацией длины двулучепреломления Λ

Особенно полезны два вида двулучепреломляющих пластин:

• пластина в пол-волны, где d = m Λ + Λ/2 и (m существующее целое);

• пластина в четверть волны, где d = m Λ + Λ/4 и . Эффектом полуволновой пластины является создание в выходном состоянии поляризации, симметричной относительно основных осей ее состоянию на входе (Рисунок A1.31).

Эта симметрия меняет направление вращения эллиптического или циркулярного состояния поляризации. Заметим, что, строго говоря, полуволновая пластинка не повернет состояние линейной поляризации, но симметризирует его относительно основных осей. Однако вращение полуволновой пластины поворачивает состоянии линейной поляризации, так же, как вращение зеркала поворачивает изображение.

Эффект четверть-волновой пластины – в изменении эллиптического состояние поляризации. В частности, когда основные оси параллельны осям эллипса, получается линейная поляризация. Наоборот, линейная поляризация дает эллиптическую поляризацию, выровненную вдоль основных осей (Рисунок A1.32). В особом случае линейной поляризации в 45 град к основным осям получается круговая поляризация.

Математически это линейное преобразование состояния поляризации является произведением матриц, известным как формализм Джонса. Состояние поляризации может быть представлено как 1× 2 столбец матрицы, и эффект пластины в умножения на квадратную матрицу 2×2. Разложение поляризации вдоль основных осей является на самом деле обычным математическим разложением по собственным осям матрицы 2×2, которая дает диагональную матрицу, с которой намного легче справиться. Эффект двулучепреломления пластины может быть записан, как

 

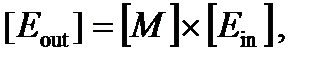(A1.172)

 

где столбцы матрицы [ E _out] и [ E _in] называются векторами Джонса: