Определение передаточных отношений в группах передач

Для определения передаточных отношений используются построенные графики частот вращения.

Передаточное отношение передачи u, определяется выражением:

 

u = j ^k, (24)

 

где k – число интервалов между горизонталями, перекрытых лучами, соединяющими отметки частот вращения на соседних валах.

 

Определение чисел зубьев передач

При определении чисел зубьев исходят из постоянства межосевого расстояния и числа зубьев, определяют по следующим формулам:

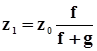, (25)

, (26)

, (27)

 (28)

 

где z ₁ и z ₂ – числа зубьев ведущего и ведомого колес;

z ₀ – сума чисел зубьев сопряженных колес;

f – числитель передаточного отношения;

g – знаменатель передаточного отношения;

K – наименьшее кратное сумм (f + g);

Е – целое число;

z_min = 18 – минимальное число зубьев.

 

В соответствии с полученными числами зубьев передач, вычерчивается вариант кинематической структуры (рисунок 16).

 

Рисунок 16 – Кинематическая структура коробки скоростей

Определение крутящих моментов на валах коробки скоростей

Крутящие моменты на валах Т, Н·м, могут быть найдены по формуле:

 

 (29)

 

где Р_эд. – мощность на валу двигателя, кВт;

h – КПД участка кинематической цепи от двигателя до рассчитываемого вала;

n – расчетная частота вращения вала, об/мин.

 

Кинематический расчет коробки скоростей выполнен с использованием программы «SIRIUS 2». Результаты расчета находятся в приложении А.

 

Расчет прямозубой эвольвентной передачи

Определение модуля зубчатой передачи расчетом на контактную выносливость зубьев

Для прямозубой цилиндрической передачи модуль m _н, мм, определяется по формуле:

 

 (30)

 

где K_d – вспомогательный коэффициент; для прямозубых передач K_d = 770;

z ₁ – число зубьев шестерни;

T ₁ – вращающий момент на шестерне, Н×м;

u – передаточное отношение передачи;

s _НР – допускаемое контактное напряжение, МПа;

K_{H b} – коэффициент, учитывающий распределение нагрузки по ширине венца;

 

 (31)

 

где b – рабочая ширина венца зубчатой передачи;

d ₁ – делительный диаметр шестерни.

 

Определение модуля зубчатой передачи расчетом на выносливость зубьев при изгибе

Для прямозубой цилиндрической передачи модуль m_F, мм, определяется по формуле:

 

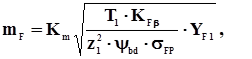  (32)

 

где K_m – вспомогательный коэффициент; для прямозубых передач K_m = 14;

K_{F b} – коэффициент, учитывающий распределение нагрузки по ширине венца при изгибе;

s _FP – допускаемое изгибное напряжение, МПа;

Y_{F 1} – коэффициент учитывающий форму зубьев шестерни.

 

Определение стандартного модуля зубчатой передачи

Из полученных расчетных значений m_H и m_F выбирается наибольшее значение и округляется в сторону увеличения до стандартного модуля по ГОСТ 9563– 60. При этом должно выполняться следующее условие:

 

m ₁ £ m ₂ £ … £ m_k, (33)

 

где m ₁ – модуль зубчатых передач группы, расположенной первой от электродвигателя;

m_k – модуль зубчатых передач группы, расположенной последней от электродвигателя.

 

Определение межосевого расстояния зубчатой передачи

Для прямозубой цилиндрической передачи межосевое расстояние А, мм, определяется по формуле:

 

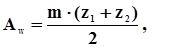 (34)

 

где m – стандартный модуль передачи, мм;

z ₂ – число зубьев зубчатого колеса, сопряженного с шестерней.

 

При определении межосевых расстояний по группам передач должно выполняться следующее условие:

 

A_{w 1} £ A_{w 2} £ … £ A_wk, (35)

 

где A_{w 1} – межосевое расстояние передач группы, расположенной первой от электродвигателя;

A_wk – межосевое расстояние передач группы, расположенной последней от электродвигателя.

Расчет прямозубой эвольвентной передачи выполнен с использованием программы «SIRIUS 2». Результаты расчета находятся в приложении Б.

Расчет и построение свертки коробки скоростей

 

Предыдущая12345678910111213Следующая

Поделиться:

Воспользуйтесь поиском по сайту: