 |
Динамические характеристики шпиндельного узла
|
|
|
|
На точность работы шпинделя оказывают влияние и динамические характеристики шпиндельного узла, которые являясь показателями динамического качества ШУ, достаточно точно определяют амплитуды колебаний переднего конца шпинделя.
Формы колебаний и их анализ позволяют наглядно представить характер деформирования основных элементов ШУ. Формы колебаний также дают представление о размере колебаний по всей длине шпинделя, что важно для правильного конструирования ШУ.
Низшие собственные частоты колебаний – важные характеристики ШУ, так как практически невозможна работа в резонансной зоне с частотой вращения, близкой к собственной частоте fс (в интервале ±20%).
Рисунок 22 – АЧХ шпиндельного узла по координате Х
Рисунок 23 – ФЧХ шпиндельного узла по координате Х
Рисунок 24 – АФЧХ шпиндельного узла по координате Х
Рисунок 24 - АЧХ шпиндельного узла по координатам Y и Z
Рисунок 25 – ФЧХ шпиндельного узла по координатам Y и Z
Рисунок 26 – АФЧХ шпиндельного узла по координатам Y и Z
Динамический анализ
Уравнение равновесия для стержневого конечного элемента, без учета гироскопического эффекта и действия центробежных сил, может быть записано в виде:
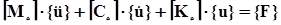(57)
где [ Ce ] – матрица коэффициентов демпфирования;
– вектор узловых скоростей;
При допущении того, что материал стержня не оказывает существенного воздействия на демпфирование колебаний, которое осуществляется, главным образом, посредством упругих демпферов (пружин), расположенных в узлах стержневого элемента, матрица коэффициентов демпфирования принимает вид:
(58)
где 
CDOF – коэффициент демпфирования по соответствующей линейной (угловой) координате, Н×с/м (Н×м×с/рад);
|
|
|
DOF – индекс, характеризующий степень свободы в рассматриваемом узле;
j – номер строки;
k – номер столбца;
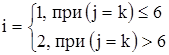– индекс узла
Матрицы [Me], [Ke], {u} и {F} идентичны матрицам, используемым при статическом анализе.
По аналогии со статическим анализом уравнение равновесия для модели, состоящей n элементов, используемое при динамическом анализе, принимает вид:
(59)
где [ Mg ] – глобальная матрица масс модели;
– глобальный вектор узловых ускорений;
[ Cg ] – глобальная матрица коэффициентов демпфирования;
– глобальный вектор узловых скоростей.
Глобальная матрица масс [Mg] формируется путем последовательного суммирования соответствующих коэффициентов в элементных матрицах, то есть:
(60)
Матрицы [Kg], 
, 
и 
формируются также как и в случае статического анализа модели. Глобальная матрица коэффициентов демпфирования получается аналогично и имеет вид:
(61)
При динамическом анализе шпиндельного узла наибольший интерес представляют его частотные характеристики, определяемые при изменении входной координаты во времени по закону гармонических колебаний. Частота этих колебаний изменяется теоретически от нуля до бесконечности, а практически – в пределах некоторого диапазона частот, который называют рабочим. Для рассматриваемой модели входной координатой является сила или момент силы. Поэтому глобальный вектор узловых нагрузок принимает следующую форму:
(62)
или
(63)
где Fmax – амплитудное значение силы (момента), Н (Н×м);
е – основание натуральных логарифмов;
– мнимая единица;
y – сдвиг силы по фазе, рад;
w – угловая скорость, рад/с;
t – время, с;
{ F 1 } и { F 2 } – вещественная и мнимая часть вектора нагрузки,
|
|
|
определяемые по формулам:
(64)
(65)
При изменении входной координаты по гармоническому закону выходная координата (перемещение) также будет изменяться гармонически. Таким образом, глобальный вектор узловых перемещений должен быть представлен в следующем виде:
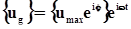(66)
или
(67)
где { umax } – амплитудное значение линейного (углового) перемещения, м (рад);
j – сдвиг перемещения по фазе, рад;
{ u 1 } и { u 2 } – вещественная и мнимая часть вектора перемещений, определяемые по формулам:
(68)
(69)
После подстановки выражений (3.61) и (3.60) в формулу (2.51) уравнение равновесия динамической модели шпиндельного узла принимает вид:
(70)
Решение полученного уравнения относительно неизвестных узловых перемещений имеет следующий вид:
(71)
Рисунок 27 – Упругая линия шпинделя
|
|
|
