Средняя гармоническая простая

Средняя гармоническая - это отношение числа вариантов признака к сумме обратных их значений. Она исчисляется по формуле

,

где х — отдельные варианты; n—их число.

Для иллюстрации области ее применения воспользуемся упрощен­ным условным примером. Предположим, в фирме, специализирующейся на торговле по почте на основе предварительных заказов, упаковкой и от­правкой товаров занимаются два работника. Первый из них на обработку одного заказа затрачивает 8 мин., второй - 14 мин. Каковы средние затраты времени на 1 заказ, если общая продолжительность рабочего времени у ра­ботников равна?

На первый взгляд, ответ на этот вопрос заключается в осреднении индивидуальных значений затрат времени на 1 заказ, т.е. (8+14):2=11 мин. Проверим обоснованность такого подхода на примере одного часа работы. За этот час первый работник обрабатывает 7,5 заказов (60:8), второй - 4,3 заказа (60:14), что в сумме составляет 11,8 заказа. Если же заменить инди­видуальные значения их предполагаемым средним значением, то общее число обработанных обоими работниками заказов в данном случае умень­шится:

Подойдем к решению через исходное соотношение средней. Для определения средних затрат времени необходимо общие затраты времени за любой интервал (например, за час) разделить на общее число обрабо­танных за этот интервал двумя работниками заказов:

Если теперь мы заменим индивидуальные значения их средней ве­личиной, то общее количество обработанных за час заказов не изменится:

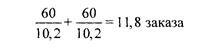
Подведем итог: средняя гармоническая не взвешенная может ис­пользоваться вместо взвешенной в тех случаях, когда значения w_i для еди­ниц совокупности равны (рабочий день у сотрудников одинаковый).

Средняя геометрическая

Этот вид средней вычисляется для установления средних по­казателей темпов роста рядов динамики.

Средняя геометрическая исчисляется путем извлечения корня степени п из произведений отдельных значений признака:

где — средняя геометрическая, n — число значений признака, а П — знак перемножения.

Предположим, годовые темпы роста продукции какого-либо предприятия составили в 1998 г. — 1,036; в 1999. — 1,069; в 2000г. — 1,084 и в 2001г. — 1,090. Тогда среднегодовой темп за четырехлетие

 

 

Необходимо иметь в виду, что средняя геометрическая может вычисляться лишь в том случае, когда на протяжении всего пе­риода происходит либо непрерывный рост, либо непрерывное па­дение. При пилообразном характере уровней ряда (т.е. их росте и па­дении — 1,05; 1,1; 1,15; 1,07; 1,3) средний темп роста имел бы фик­тивное значение.

В заключение отметим, что для вычисления рассмотренных вы­ше степенных средних необходимо использовать все имеющиеся зна­чения признака.

В ряде случаев можно определить среднюю величину без про­изводства вычислений, как бы визуально. Для этого используют такие средние величины, как мода и медиана.

Мода и медиана

Мода и медиана определяются лишь структурой распределе­ния. Поэтому их именуют структурными позиционными средними. Медиану и моду используют как среднюю характеристику в тех совокупностях, где расчет средней степенной невозможен или не­целесообразен. Для этого в качестве средней берется наиболее ча­сто встречающаяся величина, называемая модой (Мо). Например, 100 уголовных дел по определенному виду преступлений распре­делились за год по срокам расследования таким образом:

Срок расследования, месяцы	Число дел
	всего 100

 

Наибольшее число дел данной категории (наибольший вес — 60) расследуется в течение двух месяцев. Это и будет мода — ва­риант, которому соответствует наибольшая частота в совокупно­сти или в вариационном ряду.

К моде прибегают для выявления величины признака, име­ющей наибольшее распространение (цена на рынке, по которой было совершено наибольшее число продаж данного товара, но­мер обуви, который пользуется наибольшим спросом у покупате­лей, и т.д.). Мода чаще всего используется в совокупностях боль­шой численности.

Медиана (Me) — это средняя вариантов ранжированного (упоря­доченного) ряда, расположенного в определенном порядке — по воз­растанию или убыванию вариантов. Она делит такой ряд пополам.

Например, выборочное обследование в одном из округов Москвы 12 коммерческих пунктов обмена валюты позволило за­фиксировать различные цены за доллар США при его продаже (дан­ные на 17 июля 2000 г. при установленном ЦБ РФ курсе доллара США 27,85руб.)'

 

⇐ Предыдущая78910111213141516Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: