Динамика выпуска продукции на производственном объединении в 1997-2001 гг.

Год
Выпуск продукции, млн. руб.	21,2	22,4	24,9	28,6	31,6

_● Абсолютный прирост базисный определяется как раз­ность между уровнем изучаемого периода у_i, и уровнем, принимае­мым за базу сравнения у₀

= у_i - у₀

1998 г. 22,4 - 21,2 = 1,2; 2000 г. 28,6 - 21,2 = 7,4;

1999г. 24,9-21,2=3,7; 2001 г. 31,6 - 21,2 = 10,4.

Полученные абсолютные приросты показывают систематиче­ское возрастание абсолютных приростов выпуска продукции, млн.руб.

_● Абсолютный прирост цепной 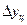определяется как разность ме­жду последующим у_i и предыдущим уровнями ряда

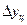=у_i - y_i-1

1998 г. 22,4 - 21,2 = 1,2 2000 г. 28,6 - 24,9 = 3,7;

1999 г. 24,9 - 22,4 = 2,5 2001 г. 31,6 - 28,6 = 3,0.

Из полученных цепных абсолютных приростов видно нараста­ние абсолютного прироста.

Темп роста базисный, % — отношение уровня изучаемого пе­риода y_i, и уровня, принимаемого за базу сравнения у₀.

1998 г. 22,4: 21,2 *100% = 105,9%; 2000 г. 28,6: 21,2*100% = 134,9%;

1999 r.24,9: 21,2 *100% ⁼ 117,5%; 2001 г. 31,6: 21,2*100% = 149,0%.

Темп роста цепной Трц% — отношение последующего уровня yi к предыдущему у_i-1.

T_рц=(y_i : y_i-1)

1998 г. 22,4: 21,2*100% = 105,9%; 2000 г. 28,6: 24,9*100% = 114,9%;

1999 г. 24,9: 22,4*100% = 111,2%; 2001 г. 31,6: 28,6*100% -= 110,5%.

Темп прироста базисный:

;

Темп прироста цепной:

;

Показатели абсолютного значения одного процента прирос­та (А%) определяются:

а) путем отношения абсолютного прироста к темпу прироста, выраженного в %;

б) 0,01 от предыдущего уровня:

1999 г. 22,4 0,01 = 0,22 млн. руб.;

2000 г. 24,9 • 0,01 = 0,25 млн. руб.;

2001 г. 28,6 • 0.01 = 0,29 млн. руб.

● Определим средний уровень ряда динамики выпуска продук­ции по средней арифметической простой, так как данный ряд динамики интервальный с равноотстоящими уровнями

млн. руб.

Это указывает на то, что в течение 1997- 2001 гг. в среднем за год выпуск продукции составил 25,74 млн. руб.

 

Средний абсолютный прирост выпуска продукции определим по формуле

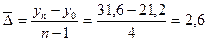млн. руб.

т. е. за период с 1997 по 2001 год в среднем ежегодно выпуск про­дукции увеличивался на 2,6 млн. руб.

Среднегодовой темп роста определим по формуле средней гео­метрической:

или 110,5%

т. е. в среднем за 1997-2001 гг. ежегодно выпуск продукции уве­личивался 1,105 раза.

Средний темп прироста равен

Тр·100% - 100% = 110,5% - 100% = 10,5%,

т. е. в среднем ежегодно за 1997—2001 гг. темп прироста выпуска продукции составлял 10,5%.

Задача 2. На основании данных табл. 5.4.3 необходимо:

Таблица 5.4.3.

Производство творога

Месяц

Производство творога, т

 

• выявить характер и тип динамики, используя графическое выравнивание;

• определить существующую тенденцию изменения, используя для этого механический и аналитический приемы;

• изобразить графически существующую тенденцию. Сделать выводы;

• осуществить анализ колеблемости (устойчивости) и объяс­нить полученные результаты.

Для анализа рядов динамики используем приемы:

§ графический — графическое выравнивание,

§ механический — укрупнение периодов, сглаживание по скользящей средней и др.. результаты механического выравнивания оформим таблицей,

§ аналитический - выравнивание по прямой, параболе 2- го порядка и т.д.

Первый прием используется для выявления характера ряда динамики; второй - для изучения тенденции развития явлений; третий - для математического выражения и количественного измере­ния существующей тенденции с целью нахождения теоретическою уровня прогнозируемого периода

Графическое выравнивание — фактические данные динамического ряда наносят на график в прямоугольной системе координат, а затем в зависимости от характера изменения явления, проводится линия (прямая или кривая), изображающая тенденции изучаемого явления. Линия проводится таким образом, чтобы по обе стороны находилось приблизительно одинаковое число точек

Прием укрупнения периодов — все уровни динамического ряда разбиваются на группы с одинаковым числом лет (3, 4, 5 и т д)

Затем для каждой группы находится средняя арифметическая

Прием сглаживания ряда путем скользящей средней — при исчислении средних каждая последующая группа образуется со сдвигом на один год. В основу расчета берут любое число лет, все зависит от характера динамики и длительности ряда

Прием аналитическою выравнивания - определение плавного уровня, т.е. основы "оси" динамики, около которой колеблются ежегодные уровни Выравнивание ведется по уравнениям прямой, параболе 2-го порядка и др.

Уравнения прямой используют в тех случаях, когда стабильно абсолютные приросты. Оно имеет следующий вид.

, где - теоретическое значение выравненного ряда,

a _o, a ₁ - параметры уравнения, а именно

а ₀ - средний теоретический уровень в периоде, предшест­вующем начальному, начальный уровень ряда,

a ₁ — средний теоретический прирост (+) или снижение (—) изучаемого показателя в каждом последующем ряду по сравнению с предыдущим.

t — порядковый номер периода

 

Уравнение параболы 2-го порядка используется тогда, когда аб­солютные приросты не стабильны, а изменяются (возрастая или снижаясь) примерно на одну и ту же величину. Оно имеет сле­дующий вид:

,

где a ₂ — ускорение прироста (+) или снижение (-)

Произведем сглаживание ряда динамики методом трехчленной скользящей средней. Взяв данные за каждые три месяца, исчислим трехчленные скользящие суммы со сдвигом на месяц (табл. 5.4.4.):

Таблица 5.4.4.

⇐ Предыдущая10111213141516171819Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: