Заработная плата рабочих цеха

Заработная плата, руб.	Число рабочих
200-400
400-600
600-800

Вычислению среднего квадратического отклонения предшествует расчет дисперсии (табл. 5.3.5).

Таблица 5.3.5.

Расчет дисперсии

Заработная плата, руб.(х)	Число рабочих (f)				f
			-190
			-10
			+210
Итого

 

1) Исчислим среднюю арифметическую взвешенную:

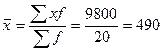руб.

2) Определим дисперсию:

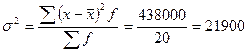руб.

3) Среднее квадратическое отклонение:

Заработная плата колеблется вокруг среднего значения - на 148 руб.

4) Коэффициент вариации величина относительная, что удобно для сравнения вариаций в любых совокупностях.

Ряды динамики

Ряды динамики позволяют изучить тенденции и закономерно­сти развития и изменения общественных явлений. Каждый ряд состоит из двух граф: в первой указываются периоды времени, во второй — числовая характеристика изучаемого явления за перио­ды.

Ряды динамики могут быть двух видов: интервальные и моментные. В интервальном ряду приводятся данные, характери­зующие размеры явления за определенные периоды времени (су­тки, месяц, год и т. д.). В моментном ряду приводятся данные, характеризующие размеры явления на определенные даты (момен­ты) времени (наличие скота на начало каждого месяца, автомо­билей на начало года и т. д.).

Следует помнить о требовании сопоставимости уровней рядов динамики. Они должны относиться к одинаковой территории, включать одинаковый круг объектов, выражаться одинаковыми единицами измерения, рассчитываться по единой методологии.

Для обобщающих характеристик рядов динамики применяется средний уровень, а для изучения интенсивности развития явлений абсолютный прирост, темп роста, темп прироста, абсолютное значение одного процента прироста.

При расчете показателей динамики сравниваемый уровень на­зывается текущим, а уровень с которым производятся сравне­ния — базисным.

Эти показатели могут рассчитываться в цепной и базисной сис­теме расчета. Базисная система расчета предполагает сравнение каждого последующего уровня с уровнем, принятым за базу,

При цепной системе расчета каждый последующий уровень сравнивается с предыдущим (табл. 5.4.1).

Таблица 5.4.1

Базисная и цепная системы расчетов показателей динамики

Показатели	Система расчета
цепная	базисная
Абсолютный прирост
Темп роста
Темп прироста
Абсолютное значение 1% прироста

У_i — текущий (сравниваемый) уровень;

У_i-1 – предыдущий уровень;

У₀ — базисный уровень.

Для обобщающей характеристики динамики рассчитываются средние показатели.

Средний уровень моментного ряда:

 

Средний уровень интервального ряда:

 

Средний абсолютный прирост:

 

Средний темп роста:

 

Средний темп прироста:

 

где п — число уровней ряда;

п - 1 — число цепных темпов роста.

Составной частью анализа динамических рядов является выяв­ление тенденций в развитии изучаемого явления.

Тенденция — это общее направление к росту, снижению или стабилизации уровней явления. Для выявления тенденции применяются следующие методы:

1) метод укрупнения периодов;

2) метод скользящей средней;

3) метод выравнивания динамического ряда по среднему абсо­лютному приросту, среднему темпу роста;

4) аналитическое выравнивание динамических рядов по урав­нениям: прямой, параболе 2-го порядка и т. д.

Задача 1. По данным табл. 5.4.2 проанализируем динамический ряд.

1. Вычислим абсолютный прирост, темп роста и темп прироста базисным и цепным методами, абсолютное значение 1 % прирос­та.

2. Определим средний уровень ряда, среднегодовой абсолют­ный прирост, среднегодовой темп роста, среднегодовой темп при­роста за 1997-2001 гг.

Таблица 5.4.2

⇐ Предыдущая9101112131415161718Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: