Динамика процентной ставки банка

t, квартал
yt,%	17,0	16,5	15,9	15,5	14,9	14,5	13,8

Требуется

а) обосновать правомерность использования среднего прироста для получения прогнозного значения процентной ставки в 8-м квартале;

б) рассчитать прогноз процентной ставки банка в 8-м квартале, используя показатель среднего прироста. Рассчитаем цепные абсолютные приросты.

 

Легко заметить, что цепные абсолютные приросты примерно одинаковы. Они незначительно варьируют от -0.4 до -0,7, что свидетельствует о близости процесса развития к линейному. По­этому представляется правомерным оценить прогнозное значение 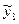с помощью среднего прироста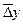

Прогнозирование по среднему темпу роста можно осуществлять в случае, когда есть основание считать, что общая тенденция ряда характеризуется показательной кривой. Для нахождения тен­денции в этом случае необходимо определить средний коэффици­ент роста, во возведенный в степень, соответствующую периоду экст­раполяции, т е. по формуле

,

где - прогнозная оценка значения уровня в точке п +1;

Y_n - фактическое значение в последней п -й точке ряда;

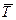- средний темп роста, рассчитанный для ряда у₁, у₂, …, у_п (не в %-м выражении).

 

Задача 4. Изменение ежеквартальной динамики процентной ставки банка происходило примерно с постоянным темпом роста в течение 7 кварталов Процентная ставка банка в первом квартале равнялась 8,3%, а в 7-м квартале — 14%.

Рассчитать прогноз процентной ставки банка в 8-м квартале, используя средний темп роста .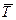

Известно, что изменение процентной ставки банка происходи­ло примерно с постоянным темпом роста в течение 7 кварталов. Следовательно, правомерно использовать средний темп роста для расчета прогноза этого показателя. Прогноз процентной ставки банка в 8-м квартале равен:

где 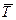берем не в процентном выражении;

 

Наиболее распространенным методом прогнозирования является аналитическое выравнивание тренда. При этом для выхода за границы исследуемого периода достаточно продолжить значения независимой переменной времени (t) в табл.5.4.6 представлены данные об остатках вкладов населения в банках за 15 месяцев.

 

Таблица 5.4.6.

Остатки вкладов населения в банках (млн. руб.) на начало месяца

Номер	yt	t	yt	t	yt

 

Для протезирования тенденции развития используем 3 модели:

линейную

параболическую

показательную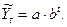

Необходимо.

1) оценить коэффициенты трендов,

2) рассчитать прогноз остатков вкладов населения в банках на один месяц вперед, т.е. на начало 16-то месяца;

3) на основе графического анализа сделать вывод о согласо­ванности трех рассмотренных моделей с исходными данными;

1) рассчитать значение критерия - средней квадратической ошибки. Выбрать лучшую модель с точки зрения указанного кри­терия.

● Для расчета коэффициентов линейного тренда воспользуемся выражениями, полученными из системы нормальных уравнений после переноса начала координат в середину ряда

В табл. 5.4.7 представлены необходимые вспомогательные вычис­ления для расчета параметров трендов.

Таблица 5.4.7. Вспомогательные вычисления

Номер месяца	yt	t	yit	t2	yit2	t4	ln yt	ln yit
		-7	-103019				9,396759	-67,1773
		-6	-99852				9,719685	-58,3181
		-5	-92520				9,825742	-49,1287
		-4	-81504				9,922113	-39,6885
		-3	-63963				9,967448	-29,9023
		-2	-46684				10,05801	-20,116
		-1	-28317				10,25122	-10,1512
							10,32954
							10,41655	10,41655
							10,5032	21,01041
							10,60965	31,82895
							10,72362	42,89448
							10,83677	54,18387
							10,93354	65,60121
							10,99173	76,94211
							154,6876	28,29541

 

Следовательно, уравнение линейного тренда имеет вид:

Согласно этой модели оценка среднего уровня ряда при t = 0 равна 33063,9 млрд. руб., а среднемесячный прирост остатков на­селения составляет 3213,9 млрд. руб.

Для прогнозирования на базе полученной модели на одну точ­ку вперед необходимо в нее подставить соответствующее значение временного параметра, т. е. t = 8. (Если бы оценки коэффициентов модели были получены без переноса начала координат в середину ряда, то следовало бы подставить в модель значение времен­ного параметра t = 16). Прогноз равен:

● Для расчета коэффициентов параболического тренда также воспользуемся выражениями, полученными из системы нормаль­ных уравнений после переноса начала координат в середину ряда

 

 

Следовательно, уравнение параболического тренда примет вид:

 

Для определения прогноза показателя надо подставить в полу­ченную модель соответствующее значение временного параметра (t = 8). Прогноз равен:

● Определяем параметры тренда, описываемого показательной функцией:

Проведя потенцирование, получаем:

a = 30106,61; b = 1,11.

Следовательно, уравнение тренда примет вид:

Согласно этой модели среднемесячный темп роста остатков вкладов населения составляет 111%. В точке, принятой за начало отсчета (t = 0), значение тренда равно 30106,61 млрд. руб. Для определения прогноза остатков вклада населения в банках на один месяц вперед подставляем в полученную модель значение t = 8.

На рис. 5.4.1 и 5.4.2 изображены графики исходного временного ряда и выравненные значения уровней, полученные на основе трех трендовых моделей: линейной, параболической и показатель­ной. На рис. 5.4.1 фактические (1) и выравненные по параболе зна­чения уровней временного ряда, на рис. 5.4.2 фактические (1), вы­равненные по прямой (2) и выравненные по показательной функ­ции (3) значения уровней временного ряда. Графический анализ свидетельствует о том, что линейную модель нельзя признать аде­кватной. Полученный же на ее основе прогноз будет сильно за­нижен. Далека от реальности и модель, рассчитанная по показа­тельной функции, а прогноз будет существенно завышен. Ближе всех к фактическим данным ложатся уровни, выравненные по параболической модели, хотя прогноз может быть несколько за­вышен.

В качестве критерия выбирается средняя квадратическая ошиб­ка:

где у_i - фактическое значение ряда;

ỹ_t - выравненное значение ряда;

п - длина ряда.

 

5.5. ИНДЕКСЫ

 

Под индексом (лат. Index) понимается относительный показатель, который характеризует соотношение уровней социально-экономического явления во времени, по сравнению с планом или в пространстве.

Индекс является результатом сравнения двух одноименных величин, числитель индексного отношения – показатели текущего периода и знаменатель – база сравнения – показатели базисного периода или плана.

Многообразие задач и исходного материала для расчетов вызывают необходимость применения разного типа индексов. Для их систематизации применяется классификация, показанная на схемах(рис.5.5.1 –5.5.6).

 

 

 

 

Рис. 5.5.1

 

 

 

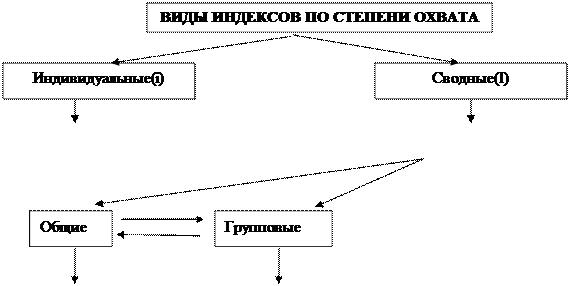
Рис.5.2

 

Индивидуальными называют индексы, показывающие степень изменения отдельных элементов сложного экономического или социально-правового явления. Например, число дорожно-транспортных происшествий в области в 2000 году составило 2400, а в 2001 году- 2000. Отношение показателя текущего периода к соответствующему показателю сравниваемого периода является индивидуальным индексом.

Индивидуальные индексы представляют собой относительные величины динамики, выполнения плана, сравнения, и их расчет не требует знания специальных правил. Формула их расчета проста:

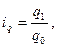
где q₁- индексируемая величина (количество ДТП) в текущем периоде (2001г.), q₀- в периоде базисном (2000г.).

В нашем примере он равен 2000/2400*100=83%.

Следовательно, за исследуемый период число ДТП сократилось на 17% (100-83).

Сводный индекс выражает соотношение величин сложного явления, состоящего из элементов, непосредственно несоизмеримых. Он характеризует изменение во времени по сравнению с планом или в пространстве всего объема исследуемого явления.

Для получения сводных индексов не может быть применено непосредственное суммирование величин для каждого из сравниваемых периодов и последующее соотношение этих сумм. Не может быть применен расчет сводного индекса на основе простой средней из индексов индивидуальных, так как в такой средней не учитывается удельный вес каждого элемента во всей совокупности.

В уголовно-правовой статистике примером сводного индекса может быть индекс преступлений, объединенных родовым объектом уголовно-правовой защиты. Исходя из структуры нового УК РФ, родовым объектом являются общественные отношения, интересы, блага, на которые посягают преступления, а нормы об ответственности за их совершение помещены в единый раздел, например преступления в сфере экономики, преступления против личности, общественной безопасности и общественного порядка и т.д. Его расчет значительно труднее, поскольку такой индекс измеряет динамику разнородных элементов совокупности, непосредственно несоизмеримых явлений.

Не останавливаясь на технике вычисления индексов на основе приведенных формул, в силу ее очевидности, укажем, что по базе сравнения все индексы можно разделить на две группы: динамические и территориальные. Первая группа индексов отражает изменение явления во времени. При их вычислении различают сравниваемый уровень и уровень, с которым производится сравнение, называемый базисным. Например индекс цен на услуги в 2001 году по сравнению с предыдущим годом; индекс тяжести последствий ДТП в 2001 году по сравнению с 2000 г. и т.п.

Выбор базы сравнения определяется целью исследования. В индексах, характеризующих изменение индексируемой величины во времени, за базисную величину принимают размер показателя в каком либо периоде, предшествующем отчетному. При этом возможны два способа расчета индексов – цепной и базисный, соответственно такие динамические индексы будут называться цепными и базисными. При базисных индексах все величины сравниваются с какой-либо одной величиной, а при цепных каждая величина сравнивается со своей предыдущей.

Очевидно, что цепные индексы могут быть применимы лишь в тех случаях, когда сравнение ведется больше чем за два периода. Если же индексы вычисляются за несколько периодов, то возникает вопрос о так называемых переменных или постоянных весах, т.е. о том, определять ли индексы за эти сроки все время на основе соизмерителей за один и тот же период или по мере перехода от одного срока к другому соответственно изменять и соизмерители (веса).

 

 

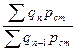
Рис. 5.3

По периоду исчисления индексы подразделяются на годовые, квартальные, месячные, недельные.

Применение цепных индексов в экономической статистике целесообразно как в случае необходимости выявления темпов исследуемой совокупности за короткие периоды времени, так и в случае изменения ассортимента выпускаемых товаров (или услуг), входящих в эту совокупность.

На их применение в уголовно-правовой статистике существенное влияние оказывают процессы введения (криминализации) или отмены (декриминализации) уголовно-правовых запретов. Так, например, анализ динамики тех или иных видов преступлений даже во временном отрезке действия одного УК сопряжен с трудностями вытекающими из частой корректировки, нестабильности его норм и статей. Что касается применения базисных индексов, то сравнивать преступность по нормам постсоциалистического уголовного права и УК РСФСР 1922, 1926 и 1960 гг. практически возможно лишь по ограниченному кругу так называемых «ядерных» преступлений – убийствам, изнасилованиям, отдельным видам корыстно-насильственных преступлений и некоторым другим.

Вторая группа индексов (территориальные) применяется для межрегиональных сравнений. Например, соотношение между максимальной и минимальной стоимостью потребительской корзины в регионах России в январе 2001 года составило 2,6 раза, между регионами европейской части России- 1,7 раза, а регионами Сибири и Дальнего Востока- 2,2 раза.

По характеру объекта исследования общие индексы подразделяются на индексы количественных (объемных) и качественных показателей. В основе такого деления лежит вид индексируемой величины. К первой группе индексов относится, например, рост преступности в целом, а ко второй- индекс тяжести последствий отдельных преступлений или преступности в целом.

 

 

 

 

Рис. 5.4

 

 

В зависимости от цели исследования и наличия исходных данных используют различные формы построения сводных индексов: агрегатную и средневзвешенную.

Агрегатный индекс - основная форма общего индекса, так как в нем отчетливо выступает отношение двух абсолютных величин, различающихся за счет изменения изучаемого явления. Латинское слово «агрегат» (aggregatus) означает «складываемый, суммируемый». Особенность этой формы индекса состоит в том, что в ней непосредственно сравниваются две суммы одноименных показателей. В настоящее время это наиболее распространенная форма индекса, используемая в практической статистике многих стран мира.

 

 

 

Рис. 5.5.

В этой связи по составу явления выделяют соответственно две группы индексов: постоянного (фиксированного) состава и переменного состава. Вопрос о том, какие из указанных индексов должны быть использованы, решается на основе экономического анализа той совокупности разнородных явлений, среднюю динамику которой должен измерить индекс.

 

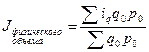
Рис. 5.6

С помощью индивидуальных индексов характеризуется изменение отдельных показателей общественных явлений и процессов.

Общая методика их расчета следующая:

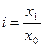
В качестве х может быть любой экономический показатель (количество продукции, цена, себестоимость и др.)

Общие индексы состоят из двух показателей- индексируемой величины (х) и веса, или коэффициента соизмерения (f).

Индексируемым показателем называют тот, измерение которого определяется.

Весом или соизмерителем называют показатель, служащий для измерения(взвешивания).

Методика конструкции общих индексов (агрегатной формы):

а) количественных показателей ;

б) качественных показателей .

Влияние факторов может быть выражено в относительных и абсолютных величинах.

При построении взаимосвязанных индексов необходимо правильно принимать веса на уровне разных периодов.

При построении индексов объемных (количественных) показателей весами берутся качественные показатели на уровне базисного периода и, наоборот, при построении индексов качественных показателей весами являются количественные показатели на уровне отчетного периода.

Принято сопровождать величины текущего периода символом 1, а базисного символом 0.

Разделим показатели на количественные (объемные) и качественные, и приведем принятую буквенную символику.

Количественные показатели

 

q₀ и q₁ - количество (объем) продукции в базисном и отчетном периодах

 

П₀ и П₁ - посевная площадь в базисном и отчетном периодах

 

 

Q₀ и Q₁ - поголовье скота, наличие техники в базисном и отчетном периодах

 

T₀ и T₁ - численность работников, затраты рабочего времени в базисном и отчетном периодах

 

Качественные показатели

 

р₀ и р₁ - цена единицы продукции в базисном и отчетном периодах

 

z₀ и z₁ - себестоимость единицы продукции в базисном и отчетном периодах

 

у₀ и у₁ - урожайность в базисном и отчетном периодах

 

Р₀ и Р₁ - продуктивность скота в базисном и отчетном периодах

 

t₀ и t₁ - затраты труда на единицу продукции в базисном и отчетном периодах

Индексы бывают индивидуальные i, которые отражают изменения отдельных элементов сложных массовых явлений, и общие J, характеризующие средние изменения массовых явлений, состоящих из непосредственно несоизмеримых элементов.

Общие индексы характеризуют соотношения уровней нескольких элементов совокупности.

По характеру индивидуальных величин индексы разделяются на индексы объемных показателей и индексы качественных показателей. К индексам объемных показателей относится индекс физического объема продукции, индекс размера посевных площадей, рост преступности в целом. К индексам качественных показателей относятся индексы цен, себестоимости, производительности труда, индекс тяжести последствий отдельных преступлений или преступности в целом и т.д. (табл.5.5.1)

Таблица 5.5.1

⇐ Предыдущая11121314151617181920Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: