 |
Интервальный вариационный ряд
|
|
|
|
Если промежуток между наименьшей и наибольшей вариантами в выборке разбить на несколько интервалов одинаковой длины и каждому интервалу поставить в соответствие число выборочных значений, попавших в этот интервал, то получим интервальный вариационный ряд. Если случайная выборкаимеет большой объем (n ≥50), а генеральная совокупность имеет непрерывное распределение, то вместо обычного (дискретного) вариационного ряда составляют именно такой ряд.
Построение интервального вариационного ряда рассмотрим на следующем примере.
Пример 1. При измерении диаметра валиков после шлифовки получены следующие результаты:
6,75; 6,77; 6,77; 6,73; 6,76; 6,74; 6,70; 6,75; 6,71; 6,72; 6,77; 6,79; 6,71; 6,78;
6,73; 6,70; 6,73; 6,77; 6,75; 6,74; 6,71; 6,70; 6,78; 6,76; 6,81; 6,69; 6,80; 6,80;
6,77; 6,68; 6,74; 6,70; 6,70; 6,74; 6,77; 6,83; 6,76; 6,76; 6,82; 6,77; 6,71; 6,74;
6,77; 6,75; 6,74; 6,75; 6,77; 6,72; 6,74; 6,80; 6,75; 6,80; 6,72; 6,78; 6,70; 6,75;
6,78; 6,78; 6,76; 6,77; 6,74; 6,74; 6,77; 6,73; 6,74; 6,77; 6.74; 6,75; 6,74; 6,76;
6,76; 6,74; 6,74; 6,74; 6,74; 6,76; 6,74; 6,72; 6,80; 6,76; 6,78; 6,73; 6,70; 6,76;
6,76; 6,77; 6,75; 6,78; 6,72; 6,76; 6,78; 6,68; 6,75; 6,73; 6,82; 6,73; 6,80; 6,81;
6,71; 6,82; 6,77; 6,80; 6,80; 6,70; 6,70; 6,82; 6,72; 6,69; 6,73; 6,76; 6,74; 6,77;
6,72; 6,76; 6,78; 6,78; 6,73; 6,76; 6,80; 6,76; 6,72; 6,76; 6,76; 6,70; 6,73; 6,75;
6,77; 6,77; 6,70; 6,81; 6,74; 6,73; 6,77; 6,74; 6,78; 6,69; 6,74; 6,71; 6,76; 6,76;
6,77; 6,70; 6,81; 6,74; 6,74; 6,77; 6,75; 6,80; 6,74; 6,76; 6,77; 6,77; 6,81; 6,75;
6,78; 6,73; 6,76; 6,76; 6,76; 6,77; 6,76; 6,80; 6,77; 6,74; 6,77; 6,72; 6,75; 6,76;
6,77; 6,81; 6,76; 6,76; 6,76; 6,80; 6,74; 6,80; 6,74; 6,73; 6,75; 6,77; 6,74; 6,76;
6,77; 6,77; 6,75; 6,76; 6,74; 6,82; 6,76; 6,73; 6,74; 6,75; 6,76; 6,72; 6,78; 6,72;
6,76; 6,77; 6,75; 6,78.
Для построения интервального ряда необходимо определить величину частичных интервалов. Считая, что все частичные интервалы имеют одну и ту же длину, для каждого интервала следует установить его верхнюю и нижнюю границы, а затем в соответствии с полученной упорядоченной совокупностью частичных интервалов сгруппировать результаты наблюдении. Длину частичного интервала h следует выбрать так, чтобы построенный ряд не был громоздким и в то же время позволял выявить характерные черты изменения значений случайной величины.
|
|
|
При большом объеме выборки вычисления становятся громоздкими, и с целью упрощения вычислений, элементы выборки объединяют в группы (разряды). Для этого интервал, содержащий все множество элементов выборки, разбивают на k непересекающихся интервалов. При этом правый конец каждого интервала исключают из соответствующего множества, а левый – включают. Ради простоты интервалы обычно выбирают одинаковой длины h = R/k, где R – размах выборки.
Просматривая результаты наблюдений, находим, что наибольшим значением случайной величины хнаиб является 6,83, а наименьшим хнаим = 6,68.
Найдем размах выборки R:
R = 6,83 – 6,68 = 0,15.
Выберем число интервалов. Для того чтобы вариационный ряд не был слишком громоздким, обычно число интервалов берут от 7 до 11. Положим предварительно k = 7, тогда длина частичного интервала
h = R/k = 0,15/7 ≈ 0,0214 ≈ 0,02.
За начало первого интервала рекомендуется брать величину
хнач = хнаим – 0,5 h.
В нашем случае хнач = 6,67.
Конец последнего интервала должен удовлетворять условию
хнач – h ≤ хнаиб < хнач.
Промежуточные интервалы получают, прибавляя к концу предыдущего интервала длину частичного интервала h (у нас h = 0,02). Просматривая результаты наблюдений, определяем, сколько выборочных значений попало в каждый конкретный интервал.
В таблице частота ni показывает, в скольких наблюдениях случайная величина приняла значения, принадлежащие тому или иному интервалу, причем нижний конец интервала входит в него, а верхний – нет. Такие частоты обычно называют интервальными, а их отношение к общему числу наблюдений – интервальными относительными частотами или частостями. Для данного примера интервальный вариационный ряд приведен в таблице 1:
|
|
|
Таблица 1
| № | [ аi; аi+ 1] | ni | ni / n = 
| Плотность частоты ni / h | Плотность частности ni / nh | xi – середина интервала |
| 6,67–6,69 | 0,01 | 0,5 | 6,68 | |||
| 6,69–6,71 | 0,075 | 3,75 | 6,7 | |||
| 6,71–6,73 | 0,085 | 4,25 | 6,72 | |||
| 6,73–6,75 | 0,22 | 6,74 | ||||
| 6,75–6,77 | 0,26 | 6,76 | ||||
| 6,77–6,79 | 0,22 | 6,78 | ||||
| 6,79–6,81 | 0,07 | 3,5 | 6,8 | |||
| 6,81–6,83 | 0,055 | 2,75 | 6,82 | |||
| 6,83–6,85 | 0,005 | 0,25 | 6,84 | |||
| ∑ |
При вычислении интервальных относительных частот округление результатов следует проводить таким образом, чтобы общая сумма относительных частот была равна 1:
∑ ni / n = 1.
По данным интервального ряда строят гистограмму частот или гистограмму относительных частот (частостей).
Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиною h,а высоты равны отношению n i/ h (плотность частоты).
Гистограммой относительных частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиною h,а высоты равны отношению ni / nh (плотность относительной частоты или частости).
На рисунке 1 построена гистограмма частостей для интервального вариационного ряда из примера 1:

Рис. 1
Пример 2. Построить гистограммы частот и относительных частот распределения, представленного таблицей.
Таблица 2
| Интервал [ аi; аi+ 1) | Частота интервала ni |
| [0;2) | |
| [2;4) | |
| [4;6) | |
| [6;8] | |
| ∑ | n = 50 |
Как видим, объем выборки n = 50, а шаг h = 2.
Таблица 3
| Интервал [ аi; аi+ 1) | Частота интервала ni | Плотность частоты ni / h | Плотность частости ni / nh | xi – середина интервала |
| [0;2) | 25/2 | 25/100 | ||
| [2;4) | 14/2 | 14/100 | ||
| [4;6) | 8/2 | 8/100 | ||
| [6;8] | 3/2 | 3/100 |
Построим гистограммы частот и относительных частот:

рис. 2
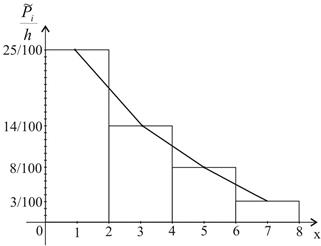
Рис. 3
Площадь гистограммы частот равна сумме всех частот, т.е. объему выборки:
S = 2∙(12,5 + 7 + 4 + 1,5) = 50.
Площадь гистограммы относительных частот равна сумме всех относительных частот, т.е. 1:
S = 2∙(0,25 + 0,14 + 0,08 + 0,03) = 1.
С увеличением объема выборки n и уменьшением длины интервала гистограмма будет стремиться к кривой плотности распределения f (x), поэтому гистограмму используют в качестве аналога оценки для плотности распределения.
|
|
|
|
|
|


