 |
Дискретный вариационный ряд. Эмпирическая функция распределения
|
|
|
|
Рассмотрим эксперимент, в результате которого наблюдается случайная величина X, с функцией распределения F (x) = P (X < x). Набор значений (x 1, x 2, …, xn) случайной величины X, полученный в результате независимых друг от друга одинаковых экспериментов, в каждом из которых наблюдается X, будет выборкойобъема n. Эту выборку можно рассматривать как случайный n -мерный вектор 
= (x 1, x 2, …, xn), где величины xi независимы и распределены так же, как случайная величина X.
Если выборочные значения x 1, x 2, …, xn расположить в порядке возрастания, то полученную последовательность называют ранжированным вариационным рядом или вариационным рядом. Таким образом, ранжированным вариационным рядом выборки (x 1, x 2, …, xn) называется такой способ ее записи, при котором элементы упорядочиваются по величине признака, т.е. последовательность записывается в виде: 
, где 
.
Разность между максимальным и минимальным элементами выборки R называют размахом выборки:
R = xn – x 1.
Среди чисел xi (i = 
) могут быть одинаковые. Различные значения случайной величины, содержащиеся в выборке, называют вариантами.
Если варианты упорядочить, т.е. расположить в порядке возрастания или убывания, а затем под каждой вариантой xi записать число ni, показывающее сколько раз она встречается в выборке, то получим таблицу, называемую дискретным вариационным (или статистическим) рядом:
Таблица 1
| x 1 | x 2 | x 3 | ... | xk |
| n 1 | n 2 | n 3 | ... | nk |
Число ni называется частотой варианты xi, а его отношение к объему выборки 
– относительной частотой (частостью) варианты xi.
Очевидно, что
.
Для наглядности строят графики дискретного вариационного ряда и, в частности, полигон частот или частостей.
|
|
|
Полигоном частот называют ломаную, отрезки которой соединяют точки (x 1; п 1), (x 2; п 2),..., (xk; nk). Для построения полигона частот на оси абсцисс откладывают варианты xi, а на оси ординат – соответствующие им частоты ni. Затем точки (xi; ni) соединяют отрезками прямых.
Полигоном относительных частот (полигоном частостей) называют ломаную, отрезки которой соединяют точки (х 1; 
), (х 2; 
), …, (хк;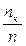 
). Для построения полигона относительных частот на оси абсцисс откладывают варианты xi, а на оси ординат – соответствующие им относительные частоты . Затем точки (xi; ) соединяют отрезками прямых.
Пример 1. Пусть имеется выборка объема n = 10:
2; 6; 2; 12; 6; 12; 2; 6; 6; 12.
Составить дискретный вариационный ряд, таблицу относительных частот и построить полигон относительных частот.
Решение. В выборке имеются различные значения 2, 6, 12, повторяющиеся соответственно 3 раза, 4 раза и 3 раза. Составим ранжированный вариационный ряд: 2; 2; 2; 6; 6; 6; 6; 12; 12; 12 и дискретный вариационный ряд:
| х | |||
| ni |
Размах выборки R = 12 – 2 = 10.
Учитывая, что объем выборки п равен 10, составим таблицу относительных частот:
| х | |||
| ni / n | 3/10 | 4/10 | 3/10 |
Построим полигон относительных частот:
Эмпирической (выборочной) функцией распределения, построенной по случайной выборке (x 1, x 2, …, xn), называется относительная частота (частость) того, что случайная величина Х примет значение, меньшее х, т. е.:
. (1)
Здесь nx – число членов ранжированного вариационного ряда, лежащих левее x.
В отличие от эмпирической функции распределения Fn (х) выборки, функцию распределения F (х) генеральной совокупности называют теоретической функцией распределения. Различие между эмпирической и теоретической функциями состоит в том, что теоретическая функция F (х)определяет вероятность события Х < х,а эмпирическая функция Fn (х) определяет относительную частоту этого же события.
|
|
|
Fn (x) – ступенчатая неубывающая функция, заданная на всей числовой оси, со скачками в точках хi. Величина скачка равна частости 
. Поскольку сумма абсолютных частот 
, то сумма относительных частот 
.
Свойства эмпирической функции распределения Fn (х) аналогичны свойствам F (х).
Пример 2. Построить эмпирическую функцию по данному распределению выборки:
| xi | |||
| ni |
Объем выборки n = 12 + 18 + 30 = 60.
хнаим = 2, значит, при х £ 2 Fn (х) = 12/60.
Значение х < 6 наблюдалось 12 раз, следовательно, при х < 6 Fn (х) = 12/60.
Значение х < 10 наблюдалось 12 + 18 = 30 раз, значит при х < 10 Fn (х) = 30/60.
Так как хнаиб = 10, то при х ³ 10 Fn (х) = 1.
Искомая эмпирическая функция имеет вид:
График строится так же, как и график интегральной функции распределения.
Найдем эмпирическую функцию распределения и для выборки из примера 1:
Построим ее график.
Выборочной медианой 
называется значение, приходящееся на середину ранжированного ряда наблюдений.
Для ранжированного вариационного ряда с нечетным числом членов медиана равна серединному элементу, а для ряда с четным числом членов – полусумме двух серединных элементов:
Медиана предпочтительнее средней арифметической для вариационного ряда, у которого крайние варианты по сравнению с остальными оказались чрезмерно большими или малыми.
Выборочной модой 
называется варианта, которой соответствует наибольшая частота.
Особенность моды как меры центральной тенденции заключается в том, что она не изменяется при изменении крайних членов ряда, т.е. обладает определенной устойчивостью к вариации признака.
В примере 1 
= 6, = 6.
В примере 2 = 10, 
.
|
|
|
