 |
Задачи для самостоятельной работы
|
|
|
|
1. Запишите выборку 5, 3, 7, 10, 5, 5, 2, 10, 7, 2, 7, 7, 4, 2, 4 в виде:
а) ранжированного вариационного, ряда; б) статистического ряда. Постройте полигон частот.
2. Постройте полигон частот выборки, представленной в виде статистического ряда. Найдите моду и размах выборки, медиану.
а)
| xi | ||||
| ni |
б)
| xi | ||||||
| ni |
3. Найдите эмпирическую функцию распределения для выборки, представленной статистическим рядом:
| xi | |||
| ni |
Выборочные характеристики
1. Выборочное среднее
Пусть (x 1, x 2, …, xn) – выборка объема n, полученная в результате n независимых наблюдений случайной величины X.
Выборочнойсредней 
, построенной по выборке X, называется величина
. (1)
Если по выборке (x 1, x 2, …, xn) построен дискретный вариационный ряд (табл. 1 п. 2.2), то
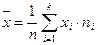, (2)
где ni – частота варианты хi.
Пример 1. В n = 10независимых экспериментах наблюдалась случайная величина X и получена выборка: 2; 10; 4; 2; 4; 4; 10; 4; 2; 10.
Вычислить выборочное среднее для X
Решение.
= 
∙(2×3 + 4×4 + 10∙3) = 5,2 – выборочное среднее.
Свойства выборочного среднего
1. Выборочное среднее постоянной равно самой постоянной:
.
2. Если все варианты увеличить (уменьшить) в одно и то же число раз, то выборочное среднее увеличится (уменьшится) во столько же раз:
= к 
.
3. Если все варианты увеличить (уменьшить) на одно и то же число, то выборочное среднее увеличится (уменьшится) на то же число:
= + С.
4. Выборочное среднее отклонений вариант от средней арифметической равно нулю:
.
5. Выборочное среднее алгебраической суммы нескольких случайных величин равно такой же сумме выборочных средних этих случайных величин:
|
|
|
.
6. Если ряд состоит из нескольких групп, общая средняя равна выборочному среднему групповых средних:
,
где – общая средняя (средняя арифметическая всего ряда);
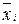– групповая средняя i -й группы, объем которой равен ni;
к – число групп.
7. В математической статистике выборочное среднее 
используется в качестве статистической оценки неизвестного математического ожидания МХ. Эта оценка является несмещенной, состоятельной и эффективной. Несмещенность означает, что 
. Состоятельность означает, что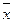 
при n ® ¥ (в силу закона больших чисел Чебышева) сходится по вероятности к МХ. Эффективность означает, что из всех оценок МХ по выборке (x 1, x 2, …, xn) имеет наименьшую дисперсию 
.
Выборочная дисперсия
На величину рассеивания наблюдаемых значений случайной величины Х вокруг их среднего арифметического будет влиять каждое отклонение хi – , однако сумма всех этих отклонений не может быть мерой рассеивания, так как эта сумма равна нулю. Чтобы на оценку меры рассеивания влияли все указанные отклонения и их знаки при этом не играли роли, целесообразно использовать не сами отклонения, а их квадраты. Лучше всего для этой цели взять среднее арифметическое величины (хi – )2, которое и называется выборочной дисперсией.
Выборочной дисперсией 
, вычисленной по выборке (x 1, x 2, …, xn), называется величина:
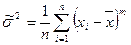, (3)
где 
– выборочная средняя x.
Если по выборке составлен дискретный вариационный ряд (табл. 1 § 2), то
, (4)
где ni – частота вариантов xi, 
– выборочное среднее.
В примере 1 из п. 2.3 вычислим двумя способами выборочную дисперсию 
,
Ранее уже была вычислена 
.
– выборочная дисперсия х, вычисленная по формуле (2).
– выборочная дисперсия х, вычисленная по формуле (4).
Свойства выборочной дисперсии 
2
1. Дисперсия постоянной равна нулю.
2. Если все варианты увеличить (уменьшить) в одно и то же число к раз, то выборочная дисперсия увеличится (уменьшится) в к 2 раз:
|
|
|
.
3. Если все варианты увеличить (уменьшить) на одно и то же число, то выборочная дисперсия не изменится:
.
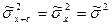4. Дисперсия равна разности между средней арифметической квадратов вариантов и квадратом средней арифметической:
.
5. Если статистический ряд состоит из нескольких групп наблюдений, то общая выборочная дисперсия равна сумме средней арифметической групповых дисперсий и межгрупповой дисперсии:
,
где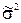 
– общая выборочная дисперсия (дисперсия всего ряда);
– средняя групповых дисперсий (среднегрупповая дисперсия);
– межгрупповая дисперсия.
Свойство 5 называют правилом сложения дисперсий.
Исправленная дисперсия. Выборочная дисперсия является смещенной оценкой генеральной дисперсии, т.е. математическое ожидание выборочной дисперсии не равно оцениваемой генеральной дисперсии, а равно
M (
) = 
.
Для исправления выборочной дисперсии достаточно умножить ее на дробь
,
получим исправленную дисперсию S 2. Исправленная выборочная дисперсия S 2 является несмещенной оценкой дисперсии генеральной совокупности σ2:
, (5)
где дробь называется поправкой Бесселя.
При малых значениях n поправка Бесселя довольно значительно отличается от единицы, с увеличением значений n она стремится к единице. При достаточно больших n выборочная и исправленная дисперсии мало отличаются, поэтому на практике исправленной дисперсией пользуются, если n < 30. Оценки 
и S 2 являются состоятельными оценками генеральной дисперсии σ2.
Для оценки среднего квадратического генеральной совокупности используют исправленное среднее квадратическое отклонение
.
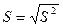Замечание. Для различных вычислений часто бывает удобней пользоваться следующей формулой для исправленной выборочной дисперсии:
.
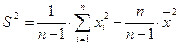Исправленную выборочную дисперсию можно считать точечной оценкой дисперсии DХ генеральной совокупности.
и S 2 являются несмещенными, состоятельными и эффективными оценками величин MХ и DХ.
|
|
|
