 |
Дискретные случайные величины. Функция распределения и числовые характеристики
|
|
|
|
Величина, которая в результате опыта или эксперимента может принимать только одно из возможных значений, называется случайной величиной (обозначим с.в.).
Дискретной случайной величиной называется такая случайная величина, которая может принимать конечное или счетное множество значений.
Примеры дискретных с. в.:
1. Количество очков, выпавшее при бросании игральной кости.
2. Число отличных оценок у студентов одной группы на экзаменах.
Непрерывной называется случайная величина, которая может принимать все значения в заданных границах или на всей числовой оси.
Примеры непрерывных с. в:
1. Время безотказной работы прибора.
2. Расстояние от центра мишени до точки попадания пули при стрельбе.
Законом распределения дискретной случайной величины X называют любое соответствие, устанавливающее связь между значениями случайной величины xi и соответствующими им вероятностями pi.
Закон распределения для дискретной с.в. X удобно задавать в виде таблицы:
| Значения X | 1 | 2 | … | n |
| Вероятности P | p 1 | p 2 | … | pn |
pi = P (X = xi), i = 1, 2,..., n, причем 
.
Графическое изображение закона распределения называется многоугольником распределения.
Наиболее употребительная форма закона распределения, одинаково пригодная для величин любого типа, связана с понятием функции распределения.
Функцией распределения (или интегральной функцией распределения) случайной величины X называется функция, определяемая равенством
F (x) = P (X < x).
Интегральная функция распределения определена для любых случайных величин, в том числе дискретных и непрерывных.
1. Функция распределения для дискретной с.в. Х вычисляется по формуле
F (x) =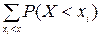 
,
где суммирование ведется по всем значениям i, для которых xi < x.
|
|
|
Свойства функции распределения F (x)
1. Все значения функции распределения F (x) принадлежат отрезку [0, 1]:
0 ≤ F (x) ≤ 1 для любого x Î (–∞; +∞).
2. F (x) – неубывающая функция, т.е. если x 1 < x 2Þ F (x 1) ≤ F (x 2).
3. F (– ∞) = 0, F (+ ∞) = 1.
4. Функция F (x) в точке x 0 непрерывна слева:
.
5. Если все возможные значения случайной величины X принадлежат бесконечному интервалу (– ∞; +∞), то
, 
.
6. Вероятность того, что X попадет в интервал (a; b):
P (a < X < b) = F (b)– F (a). (1)
Пример 1. Монету подбрасывают 3 раза. Пусть Х – число выпавших гербов. Найти функцию распределения F (x).
Решение. Величина Х может принимать значения: 0, 1, 2, 3.
Событие Ai = {выпал герб при i- м подбрасывании}, соответственно 
= {выпала решка при i- м подбрасывании}.
В результате трех подбрасываний возможно 8 элементарных исходов:
, 
, 
, 
, 
, 
, 
, 
.
В силу независимости событий Ai и 
находим соответствующие вероятности:
,
,
,
.
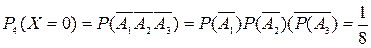Следовательно, закон распределения имеет вид:
| X | ||||
| P | 1/8 | 3/8 | 3/8 | 1/8 |
Используя определение функции распределения, вычислим ее для нашей задачи и построим график.
Если x ≤ 0, то F (x)= 0 (по условию задачи событие X < 0 невозможное, следовательно, его вероятность равна нулю).
Если 0 < x ≤ 1, то F (x)= 1/8 (X может принять значение 0 с вероятностью 1/8).
Теперь возьмем число x 0Î (1; 2]. В этом случае событие X < x 0 означает, что X может принять 2 значения: либо 0 с вероятностью 1/8, либо 1 с вероятностью 3/8. Поскольку данные события несовместны, то вероятность их суммы равна сумме их вероятностей, т.е. 1/8 + 3/8 = 1/2.
Таким образом, если 1< x ≤ 2, то F (x) = 1/2.
Аналогично если 2 < x ≤ 3, то F (x)= 1/8 + 3/8 + 3/8 = 7/8.
Если x > 3, то F (x)= 1/8 + 3/8 + 3/8 + 1/8 = 1.
Итак, функция распределения имеет вид:
F (x) = 
Построим график F (x):
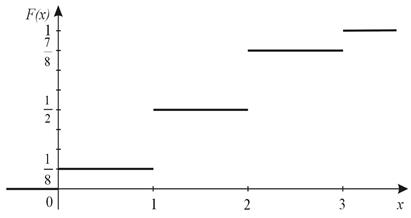
2. Математическим ожиданием M(X) дискретной случайной величины Х называется ее среднее значение, вычисленное по формуле
|
|
|
M (X) =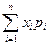 
. (2)
Как видим, математическое ожидание случайной величины – это сумма произведений всех возможных значений случайной величины на вероятности соответствующих значений.
Свойства математического ожидания M (X)
1. Математическое ожидание постоянной величины равно самой постоянной:
M (C) = C для любого C = const.
2. Постоянный множитель можно выносить за знак математического ожидания:
M (СX) = СM (X) для любого С = const.
3. Математическое ожидание суммы двух любых случайных величин равно сумме математических ожиданий слагаемых:
M (X + Y) = M (X) + M (Y).
Следствие. Математическое ожидание суммы конечного числа случайных величин равно сумме их математических ожиданий:
М (Х 1 + Х 2 +...+ Хп) = М (Х 1) + М (Х 2) +... + М (Хп).
4. Математическое ожидание линейной функции Y = ax + b случайной величины Х равно той же линейной функции от математического ожидания величины Х (следует из 2-го и 3-го свойств):
M (Y) = aM (X) + b,
где a, b – два произвольных постоянных числа.
5. Математическое ожидание суммы постоянной и случайной величины равно сумме постоянной величины и математического ожидания случайной величины:
M (С + X) = C + M (X).
6. Математическое ожидание произведения двух независимых случайных величин равно произведению математических ожиданий этих величин:
M (X × Y) = M (X) ×M (Y).
7. Математическое ожидание неотрицательной случайной величины неотрицательно:
X ≥ 0 Þ M (X) ≥ 0.
Замечание. Математическое ожидание больше наименьшего и меньше наибольшего возможных значений случайной величины. Другими словами, на числовой оси возможные значения случайной величины расположены слева и справа от математического ожидания. В этом смысле математическое ожидание характеризует расположение распределения и поэтому его часто называют центром распределения.
3. Дисперсией дискретной случайной величины Х называют число
D(X)= M (X – M (X))2, (3)
т.е. математическое ожидание квадрата отклонения случайной величины Х от ее математического ожидания M (X).
Свойства дисперсии D (X)
1. Дисперсия постоянной величины С равна нулю:
D (С) = С.
2. Дисперсия суммы двух независимых случайных величин равна сумме дисперсий этих величин:
D (X + Y) = D (X) + D (Y).
Следствие. Если Х 1, Х 2, …, Хn –случайные величины, каждая из которых независима от суммы остальных, то
|
|
|
D (Х 1 + Х 2 +... + Хn) = D (X 1) + D (X 2) +... + D (Xn).
3. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат:
D (СX) = С 2 ×D (X).
4. Дисперсия суммы постоянной и случайной величин равна дисперсии случайной величины:
D (С + X) = D (X).
Замечание. Если случайная величина Х принимает конечное число значений, то
D (X) = (x 1 – M (X))2 × p 1+ (x 2 – M (X))2 × p 2+... + (xn – M (X))2 × pn.
При вычислении дисперсии иногда удобно пользоваться формулой
D (X) = M (X2) – (M (X)) 2. (4)
Средним квадратическим отклонением случайной величины Х называется корень квадратный из дисперсии
σ(X) = 
. (5)
Пример 2. Дан закон распределения дискретной случайной величины Х.
| Значения X | ||||||
| Вероятности P | 0,2 | 0,25 | 0,3 | 0,1 | 0,1 | 0,05 |
Найти M (X), D (X), σ(X).
Решение. Математическое ожидание вычислим по формуле (2):
M(X)= 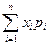= 2×0,2 + 4×0,25 + 5×0,3 + 6×0,1 + 8×0,1 + 9×0,05 = 4,75.
Для вычисления дисперсии по формуле (4) сначала найдем M (X 2):
M (X 2) = 4×0,2 + 16×0,25 + 25×0,3 + 36×0,1 + 64×0,1 + 81×0,05 = 26,35.
Тогда
D (X) = M (X 2) – (M (X)) 2 = 26,35 – (4,75)2= 3,7875.
Величину σ(X) вычислим по формуле (5):
σ(X) = 
≈ 1,9462.
Рассмотрим часто встречающиеся дискретные распределения.
1. Биномиальное распределение. Пусть производится n независимых опытов, в каждом из которых событие А появляется с вероятностью р. Говорят, что случайная величина Х, равная числу появлений события А, распределена по биномиальному закону
Pn (X = m) = 
× pm × qn – m, (6)
причем
p + q = 1.
Дисперсия:
M (X) = np
Математическое ожидание:
D (X) = npq.
Биномиальный закон распределения часто применяется в условиях, когда число независимых испытаний велико. Вычисление вероятностей по формуле (5) при этом усложняется. Поэтому представляет интерес асимптотическое приближение для биномиального закона, справедливое при больших n.
Здесь могут встретиться два случая:
1) когда n → ∞, математическое ожидание np тоже неограниченно возрастает (случай постоянного р); при этом биномиальное распределение сходится к нормальному закону, который будет рассматриваться позднее;
|
|
|
2) при n → ∞ произведение np = λ, то есть математическое ожидание рассматриваемой случайной величины, остается конечным (это означает, что вероятность события p = λ/ n стремится к нулю). В данном случае распределение сходится к распределению Пуассона.
2. Распределение Пуассона. Случайная величина Х называется распределенной по закону Пуассона, если ее возможные значения равны 0, 1, 2,..., а соответствующие вероятности определяются формулой
Pn (X = m) ≈ 
(m = 0, 1,...).
Здесь, в отличие от биномиального распределения, случайная величина может принимать бесконечное число значений.
Математическое ожидание:
D (X) = λ.
Дисперсия:
M (X) = λ.
3. Геометрическое распределение. Пусть производится n независимых испытаний, в каждом из которых событие А может наступить с вероятностью р. Испытания заканчиваются сразу, как только появилось А. Обозначим через Х случайную величину, равную числу испытаний, которые необходимо провести до первого появления события А.
Тогда
Pn (X = m) = (1– p) m × p, m= 0, 1, 2,..., n.
Распределение называется геометрическим, т.к. вероятности Pi (X = m) образуют геометрическую прогрессию.
Математическое ожидание:
M (X) = 
.
Дисперсия:
D (X) = 
.
|
|
|
