 |
Непрерывные случайные величины. Плотность распределения
|
|
|
|
Основной формой закона распределения непрерывной случайной величины является плотность вероятности.
Если функция распределения F (x) для всех x Î (– ∞; + ∞) представима в виде
F (x) = P (X < x) = 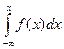 , (1)
, (1)
то функция f (х) называется плотностью распределения вероятностей (или дифференциальной функцией распределения) случайной величины X.
Свойства плотности распределения f (x)
1. Плотность распределения f (x) – неотрицательная функция, т.е.
f (x) ≥ 0 при всех x Î (– ∞; + ∞).
2. В точках дифференцируемости функции распределения F (x) ее производная равна плотности распределения:
f (x) = F′ (x)
(производная интегральной функции равна дифференциальной функции).
3. Интеграл по бесконечному промежутку (– ∞, + ∞) от плотности распределения f (x) равен единице:
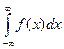 = 1.
= 1.
4. Вероятность попадания значений случайной величины X в интервал (а, b) равна определенному интегралу от плотности распределения f (x) по отрезку [ а, b ]:
P (a < X < b) = 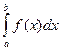 .
.
Если непрерывная случайная величина задана плотностью f (x), то график функции y = f (x) называется кривой распределения вероятностей этой с.в. (или кривой вероятности).
Для непрерывной с.в. Х справедливо:
P (a ≤ X < b) = P (a < X < b) = P (a < X ≤ b) = P (a ≤ X ≤ b), (2)
т.е. вероятность попадания случайной величины в интервал (a; b) не зависит от того, является этот интервал открытым или закрытым.
Математическое ожидание непрерывной с.в. Х:
M (X) = 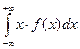 . (3)
. (3)
Дисперсия непрерывной с.в. Х:
D (X) = M (X – M (X)) = 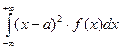 . (4)
. (4)
или
D (X) = M (X 2 ) – M (X) 2 = 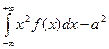 . (5)
. (5)
Рассмотрим часто встречающиеся законы распределения, имеющие плотность.
1. Равномерное распределение. С.в. Х называется равномерно распределенной на отрезке [ a; b ], если ее плотность вероятности определяется формулой:
|
|
|
f (x) = 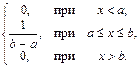
График функции плотности вероятности равномерно распределенной с.в. изображен на рисунке 1.
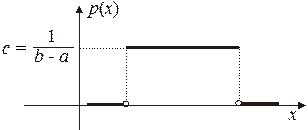
Рис. 1
Функция распределения данной случайной величины:
F (x) = 
График функции F (x)изображен на рисунке 2.

Рис. 2.
Математическое ожидание:
M (X) = 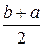 ;
;
Дисперсия:
D (X) = 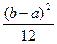 .
.
Среднее квадратическое отклонение:
σ(X) = 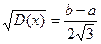 .
.
Вероятность того, что случайная величина Х, распределенная по равномерному закону, примет значение, лежащее в интервале (α, β):
P(α < X < β) = 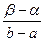 .
.
Геометрически эта вероятность представляет собой заштрихованную площадь на рисунке 3.

Рис 3.
2. Показательное распределение. Непрерывная с.в. Х распределена по показательному закону, если ее плотность вероятности имеет вид
f (x) = 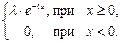
График плотности вероятности с.в. Х, распределенной по показательному закону, изображен на рисунке 4.
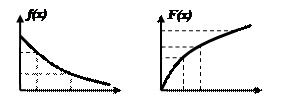
Рис. 4 Рис. 5
Функция распределения данной случайной величины:
F (x) = 
График функции F (x)изображен на рисунке 5.
Математическое ожидание: M (X) = 1/λ.
Дисперсия D (X) = 1/λ2.
Среднеквадратичное отклонение σ(X) = 1/λ.
Вероятность попадания в интервал (α, β) непрерывной случайной величины Х, которая распределена по экспоненциальному (показательному) закону:
P (α < X < β) = e – λα – e – λβ.
3. Нормальное распределение. С.в. Х (– ∞ < x < + ∞) называется нормально (по закону Гаусса) распределенной, если ее плотность вероятности определяется формулой
f (x) =  ,
,
где а, σ– параметры распределения: а – математическое ожидание, σ – среднее квадратичное отклонение с. в. Х.
График функции f(x) называют нормальной ( или гауссовой) кривой. Нa рисунке 6 изображена нормальная кривая при а = 10 и σ = 5.

Рис. 6
Изменение среднего квадратического отклонения при фиксированном значении математического ожидания приводит к изменению формы кривой распределения. С уменьшением σ вершина кривой распределения будет подниматься, кривая будет более «островершинной» (вытянутой вдоль оси симметрии); с увеличением σ кривая распределения менее «островершинна» и более растянута вдоль оси абсцисс. Одновременное изменение параметров a и σ приведет к изменению и формы, и положения кривой нормального распределения.
|
|
|
Найдем математическое ожидание нормально распределенной с.в., используя формулу
M (X) =  .
.
Для вычисления интеграла произведем замену 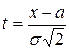 :
:
М (Х) = а.
Используя формулу
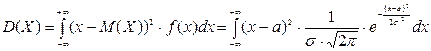
(для вычисления интеграла произведем ту же замену, как и при вычислении предыдущего интеграла), найдем дисперсию нормально распределенной с.в.:
D (Х) = σ2.
При а = 0 и σ = 1 (т.е. Х ~ N (0; 12) нормальное распределение называют стандартным (нормированным) нормальным распределением. Обозначим плотность такого распределения через φ (x), т.е.
φ (x) = 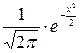 .
.
Значения φ (x) можно найти в таблицах (см. приложение 1).
График кривой стандартного нормального распределения выглядит следующим образом:
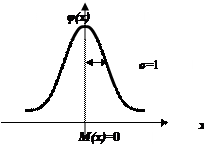
Рис. 7
Свойства функции φ ( x )
1. Функция φ (x) – четная, т.е. φ (– х) = φ (x).
2. С увеличением аргумента х по абсолютной величине φ (x) монотонно убывает и при х → ∞ имеет пределом нуль.
3. При х = 4 f (х) = 0,0001, при х = 5 φ (x) = 0,0000015, поэтому при │ х │> 5 можно считать, что φ (x) = 0. В связи с этим таблицы ограничиваются значениями функции φ (x) для аргументов х = 4 или х = 5.
4. Максимальное значение функция φ (x) принимает при х = 0, т. е. φ (x) = 0,3989.
Любая нормально распределенная случайная величина может быть преобразована в стандартную (нормированную) нормально распределенную случайную величину. Математическое преобразование достигается вычитанием a из x, а затем делением результата на σ:
Хстанд. = 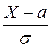 .
.
Тогда обратное преобразование стандартной нормальной с.в.:
X = a + Хстанд ×σ.
Вероятность того, что случайная величина Х, распределенная по нормальному закону, примет значение, лежащее в интервале [α, β):
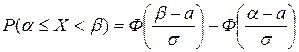 ,
,
где функция Φ(x) = 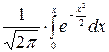 – первообразная функции φ (x). Ее называют функцией Лапласа. Значения Φ(x) можно найти в таблицах (см. приложение 2). При использовании таблиц необходимо учесть, что:
– первообразная функции φ (x). Ее называют функцией Лапласа. Значения Φ(x) можно найти в таблицах (см. приложение 2). При использовании таблиц необходимо учесть, что:
1. Φ(x) – нечетная функция, т.е. Φ(– x) = – Φ(x).
2. При x = 0 функция Лапласа равна нулю: Φ(x) = 0.
|
|
|
3. При x > 5 полагают Φ(x) = 0,5.
График функции Φ(x)изображен на рисунке 8.
 | |||
| |||
Рис. 8
Вероятность того, что абсолютная величина отклонения случайной величины Х от ее математического ожидания меньше положительного числа α, равна
P (| X – a | < α) = 2Φ 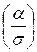 .
.
Если в этой формуле принять α = 3 σ, то
P (| X – a)| < 3 σ = 2Φ(3) ≈ 0,9973.
Иначе говоря, событие, состоящее в том, что нормально распределенная случайная величина Х с параметрами а и σ принимает значения из интервала (а – 3σ; а + 3σ), является почти достоверным (с вероятностью 0,9973). На этом основано правило трех сигм, которое часто применяется в статистике. Его можно сформулировать так: если случайная величина распределена по нормальному закону, то модуль ее отклонения от математического ожидания практически не превышает утроенного среднеквадратического отклонения.
Пример 1. С.в. Х задана интегральной функцией:
F (x) = 
Построить график интегральной функции распределения. Найти f (x) и вероятность того, что в результате испытания с.в. X примет значения на отрезке [1; 1,5].
Решение. Построим график интегральной функции:

По определению f (x) = F′ (x):
f (x) = 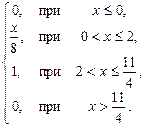
Вероятность попадания с.в. X на отрезок [1; 1,5] находим, используя 4-е свойство плотности распределения f (x) и формулу (2):
P (1 ≤ X ≤ 1,5) = 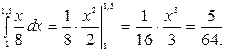
Замечание. Вероятность попадания с.в. X на отрезок [1; 1,5] можно найти, используя 6-е свойство интегральной функции распределения F (х):
P (1 ≤ X ≤ 1,5) = F (1,5) – F (1) =  .
.
Пример 2. Дана функция плотности распределения:
f (x) = 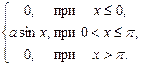
Найти параметр а, интегральную функцию распределения случайной величины Х, ее математическое ожидание, дисперсию и среднеквадратичное отклонение.
Решение. Для нахождения параметра а воспользуемся 3-м свойством f (x):
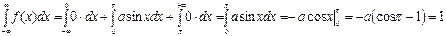
Отсюда a = 1/2.
Для нахождения интегральной функции распределения F (x) воспользуемся формулой (1).
Если x ≤ 0, то F (x) = 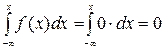 ;
;
если 0< x ≤ π, то F (x) = 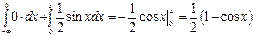 ;
;
если x > π, то F (x) = 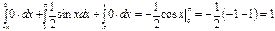 .
.
Таким образом,
F (x) = 
Математическое ожидание с.в. Х находим по формуле (3)
|
|
|
M (X) = 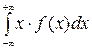 =
= 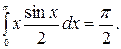
Дисперсию с.в. Х находим по формуле (5)
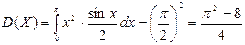 ≈ 5,8415.
≈ 5,8415.
Среднеквадратичное отклонение:
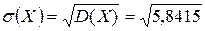 ≈ 2,4169.
≈ 2,4169.
|
|
|


