Задачи для самостоятельной работы

1. Величина Х распределена нормально с параметрами а = 5, σ = 1. Найти вероятность того, что Х примет значение в интервале (4; 7).

Отв.: 0,8185.

2. Случайная величина Х задана функцией плотности f (x) = c (x ² + 2 x) в интервале (0, 1); вне этого интервала f (x) = 0. Найти: а) параметр с; б) математическое ожидание величины Х.

Отв.: а) 3/4; б) 11/16.

4. Найти математическое ожидание случайной величины Х, заданной функцией распределения:

F (x) =

Отв.: 2.

Двумерные дискретные случайные величины

 

Совокупность двух случайных величин (X, Y), рассматриваемых совместно, называется системой двух случайных величин.

Например, показатели веса и роста ребенка могут быть записаны в виде системы (Х ₁, Х ₂), где Х ₁– вес, Х ₂– рост.

Очень часто результат испытания характеризуется не одной случайной величиной, а системой случайных величин Х ₁, Х ₂, …, Х_n, которую называют также многомерной (n-мерной) случайной величиной или случайным вектором Х = (Х ₁, Х ₂, …, Х_n).

Геометрически двумерную (X, Y) и трехмерную (X, Y, Z) случайные величины можно изобразить случайной точкой или случайным вектором плоскости Оxy или трехмерного пространства Оxyz. В случае n -мерного пространства (n > 3) также говорят о случайной точке или случайном векторе этого пространства.

Рассмотрим более подробно двумерные дискретные случайные величины.

Пусть (X, Y) – двумерная дискретная с.в. Закон ее распределения можно представить в виде таблицы (матрицы) распределения, в каждой клетке которой располагаются вероятности произведения событий p_ij = P (X = x_i)× P (Y = y_j), i = 1, 2,..., n; j = 1, 2,..., m:

 

Х Y	y 1	...	yj	...	ym
x 1	p1 1	...	p1j	...	p1m
...	...	...	...	...	...
xi	pi 1	...	pij	...	pim
...	...	...	...	...	...
xn	pn 1	...	pnj	...	pnm

 

Заметим, что

p_i = P (X = x_i) = и p_j = P (Y = y_j) = .

Сумма всех элементов таблицы равна 1:

= 1.

Зная закон распределения (X, Y), можно найти законы распределения X и Y по отдельности. Для определения вероятностей p_i = P (X = x_i) надо в таблице просуммировать вероятности в i -й строке, а для определения вероятности p_j = P (Y = y_j) просуммировать вероятности в j -м столбце.

Пример 1. Дан закон распределения дискретной двумерной с.в. (X, Y):

XY
	0,25	0,15	0,15
	0,05	0,05	0,35

 

Найти: законы распределения X и Y по отдельности.

Решение. а) Случайная величина X может принимать значения:

X = 1 с вероятностью р ₁= 0,25 + 0,15 + 0,15 = 0,55;

X = 2 с вероятностью р ₂= 0,05 + 0,05 + 0,15 = 0,45.

Отсюда закон распределения X:

Х
P	0,55	0,45

Аналогично закон распределения Y:

Y
P	0,3	0,2	0,5

 

Схема Бернулли

 

Схема Бернулли заключается в следующем. Проводится n последовательных, независимых друг от друга, одинаковых испытаний, в каждом из которых может наступить или не наступить событие A. Так как испытания одинаковы, то в любом из них событие A наступает с одинаковой вероятностью, обозначим ее p = P (A). Вероятность противоположного события обозначим q. Тогда q = 1 – p. Наступление события A обычно называют успехом, а ненаступление – неудачей.

Вероятность того, что в n независимых испытаниях событие A появится ровно m раз, определяется по формуле Бернулли

P_n (m) = . (1)

Теорема 1. Вероятность появления хотя бы одного из событий A ₁, A ₂ ,... A_n, независимых в совокупности, равна

P (A) = 1 – q₁ q₂... q_n, (2)

где q ₁, q₂, ..., q_n – вероятности противоположных событий .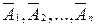

Следствие. Если события A₁, A₂,... A_n имеют равные вероятности p, то вероятность появления хотя бы одного из этих событий

P (A) = 1 – qⁿ. (3)

Вероятность того, что в n независимых испытаниях в условиях схемы Бернулли событие A появится не менее m ₁ раз и не более m ₂ раз, обозначается P_n (m ₁ ≤ m ≤ m ₂) и вычисляется по формуле

P_n (m ₁ ≤ m ≤ m ₂)= P_n (m ₁) + P_n (m ₁+1) + ... + P_n (m ₂).

Пример 1. В мастерской работает 4 мотора. Для каждого мотора вероятность перегрева к обеденному перерыву равна 0,8. Найти вероятность того, что к обеденному перерыву:

а) перегреются 2 мотора;

б) перегреется хотя бы один мотор;

в) перегреются все моторы;

г) ни один мотор не перегреется;

д) перегреется не более 2 моторов.

Решение. а) Найдем вероятность того, что перегреются 2 мотора из четырех. События A = {мотор перегреется} и = {мотор не перегреется} – противоположные. Пусть

P (A) = p, 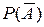= q.

Очевидно, что

q = 1 – p = 1 – 0,8 = 0,2.

Поскольку для каждого мотора p (A) постоянна, то имеет место формула Бернулли:

P ₄(2) = = 0,1536.

б) Найдем вероятность того, что перегреется хотя бы один мотор из четырех. Воспользуемся формулой (3):

P ₄(m ≥ 1) = 1 – q ⁴ = 1– 0,2⁴ = 0,9984.

в) Найдем вероятность того, что перегреются все моторы:

P ₄(4) = (0,8)⁴ = 0,4096.

г) Найдем вероятность того, что не перегреется ни один мотор:

P ₄(0) = (0,2)⁴ = 0,0016.

д) Событие {перегреется не более 2 моторов} означает, что перегреются либо 1, либо 2, либо ни одного мотора. Используем теорему сложения несовместных событий:

P ₄(m ≤ 2) = P ₄(0) + P ₄(1) + P ₄(2) = 0,0016 + 0,0282 + 0,1536 = 0,1834.

Значение m = m₀, при котором вероятность (1) принимает наибольшее значение, называется наивероятнейшим числом успехов и удовлетворяет двойному неравенству

np – q ≤ m ₀ ≤ np + p, (4)

причем:

1. Если np – q – целое число, то m₀ принимает два значения.

2. Если np – q – дробное число, то m₀ принимает единственное значение.

3. Если np – целое число, то m₀ = np.

Пример 6. Вероятность попадания в цель стрелком при одном выстреле равна 0,8. Найти наивероятнейшее число попаданий при 100 выстрелах.

Решение. По условию n = 100; p = 0,8; q = 0,2. Подставив данные задачи в неравенство (4), получим

100×0,8 – 0,2 ≤ m₀ ≤ 100×0,8 + 0,8.

Отсюда 79,8 ≤ m ₀≤ 80,8 Þ m ₀= 80 – единственное целое число, удовлетворяющее данному неравенству.

⇐ Предыдущая567891011121314Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: