 |
Указания к выполнению контрольной работы №1
|
|
|
|
МИНИСТЕРСТВО СЕЛЬСКОГО ХОЗЯЙСТВА РФ
Федеральное агентство по сельскому хозяйству РФ
ФГОУ ВПО
«Орловский государственный агарный университет»
Кафедра «Математика»
Высшая математика
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
И КОНТРОЛЬНЫЕ ЗАДАНИЯ
Для студентов-заочников инженерно-технических специальностей сельскохозяйственных высших учебных заведений
Орёл, 2005
Автор: Моисеенко А.М.
Высшая математика: Методические указания и контрольные задания для студентов -заочников инженерно-технических специальностей сельскохозяйственных высших учебных заведений. Орел, 2006 г.
Высшая математика
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
И КОНТРОЛЬНЫЕ ЗАДАНИЯ
Для студентов-заочников инженерно-технических специальностей сельскохозяйственных высших учебных заведений
Предисловие
Настоящее пособие предназначено для студентов-заочников инженерно-технических специальностей сельскохозяйственных высших учебных заведений, для которых учебным планом предусмотрено изучение курса высшей математики в объеме
Пособие содержит краткие указания к выполнению каждой из шести контрольных работ, а также решения некоторых задач, тщательный разбор которых поможет студенту-заочнику выполнить соответствующую контрольную работу. Контрольные работы составлены по двадцативариантной системе. Это позволило отразить в них более широкий круг вопросов программы.
Общие методические указания
ПОРЯДОК ВЫПОЛНЕНИЯ
КОНТРОЛЬНЫХ РАБОТ
На первом курсе обучения студенты-заочники выполняют работы 1, 2, 3; на втором курсе – работы 4, 5, 6.
|
|
|
К выполнению каждой контрольной работы следует приступать только после изучения соответствующего материала курса по учебнику и решения задач, указанных в каждой теме. Следует также внимательно разобрать решения тех задач, которые приводятся в данном пособии к каждой теме. При этом следует руководствоваться следующими указаниями:
1. Каждую работу следует выполнять в отдельной тетради, на внешней обложке которой должны быть указаны фамилия и инициалы студентов, полный шифр, номер контрольной работы и дата ее отправки в институт. Решения всех задач и пояснения к ним должны быть достаточно подробными. При необходимости следует делать соответствующие ссылки на вопросы теории с указанием формул, теорем, выводов, которые используются при решении данной задачи. Все вычисления (в том числе и вспомогательные) необходимо делать полностью. Чертежи и графики должны быть выполнены (желательно на миллиметровой бумаге) аккуратно и четко с указанием единиц масштаба, координатных осей и других элементов чертежа. Объяснения к задачам должны соответствовать тем обозначениям, которые даны на чертеже.
Для замечаний преподавателя необходимо на каждой странице оставлять поля шириной 3-4 см.
2. После получения работы (как зачтенной, так и незачтенной) студент должен исправить в ней все отмеченные рецензентом недостатки. В случае незачета студент обязан в кратчайший срок выполнить все требования рецензента и представить работу на повторное рецензирование, приложив при этом первоначально выполненную работу.
3.Контрольные работы должны выполняться самостоятельно. Если будет установлено, что та или иная контрольная работа выполнена несамостоятельно, то она не будет зачтена, даже если в этой работе все задачи решены верно.
4. В период экзаменационной сессии студент обязан представить все прорецензированные и зачтенные контрольные работы. При необходимости (по требованию преподавателя) студент должен давать на экзамене устные пояснения ко всем или некоторым задачам, содержащимся в этих работах.
|
|
|
5. Студент выполняет тот вариант контрольных работ, который совпадает с последней цифрой его учебного шифра. При этом если предпоследняя цифра учебного шифра есть число нечетное (1, 3, 5, 7, 9), то номера задач для соответствующего варианта даны в таблице 1 (с. данного пособия); если же предпоследняя цифра учебного шифра есть число четное или ноль (2, 4, 6, 8, 0), то номера задач для соответствующего варианта даны в таблице 2 (с. пособия).
КОНСУЛЬТАЦИИИ
Если в процессе изучения материала или при решении той или иной задачи у студента возникают вопросы, на которые он не может ответить сам, то можно обратиться к преподавателю для получения письменной или устной консультации. В случае письменной консультации в запросе следует возможно более точно указать характер затруднения. При этом обязательно следует где указать полное название книги, год издания и страницу, где трактуется непонятный для студента вопрос или помещена соответствующая задача.
Задания для контрольных работ по математике
Для студентов заочной формы обучения
Контрольная работа №1
1 - 10. Даны векторы а (а1; а2; а3), b (b1; b2; b3), с (с1; с2; с3) и d (d1; d2; d3) в некотором базисе. Показать, что векторы а, b, c образуют базис, и найти координаты вектора d в этом базисе.
1. а (1;2;3), b (-1;3;2), с (7;-3;5), d (6;10;17).
2. а (4;7;8), b (9;1;3), с (2;-4;1), d (1;-13;-13).
3. а (8;2;3), b (4;6;10), с (3;-2;1), d (7;4;11).
4. а (10;3;1), b (1;4;2), с (3;9;2), d (19;30;7).
5. а (2;4;1), b (1;3;6), с (5;3;1), d (24;20;6).
6. а (1;7;3), b (3;4;2), с (4;8;5), d (7;32;14).
7. а (1;-2;3), b (4;7;2), с (6;4;2), d (14;18;6).
8. а (1;4;3), b (6;8;5), с (3;1;4), d (21;18;33).
9. а (2;7;3), b (3;1;8), c (2;-7;4), d (16;14;27).
10. а (7;2;1), b (4;3;5), с (3;4;-2), d (2;-5;-13).
11 - 20. Даны координаты вершин пирамиды А1А2А3А4. Найти 1) длину ребра А1А2; 2) угол между ребром А1А2 и А1А4; 3) угол между ребрами А1А4 и гранью А1А2А3; 4)площадь грани А1А2А3; 5) объем пирамиды; 6) уравнение прямой А1А2; 7) уравнение плоскости А1А2А3; 8) уравнение высоты, опущенной из вершины А4 на грань А1А2А3. Сделать чертеж.
11. А1 (4;2;5), А2 (0;7;2), А3 (0;2;7), А4 (1;5;0).
12. А1 (4;4;10), А2 (4;10;2), А3 (2;8;4), А4 (9;6;4).
13. А1 (4;6;5), А2 (6;9;4), А3 (2;10;10), А4 (7;5;9).
14. А1 (3;5;4), А2 (8;7;4), А3 (5;10;4), А4 (4;7;8).
|
|
|
15. А1 (10;6;6), А2 (-2;8;2), А3 (6;8;9), А4 (7;10;3).
16. А1 (1;8;2), А2 (5;2;6), А3 (5;7;4), А4 (4;10;9).
17. А1 (6;6;5), А2 (4;9;5), А3 (4;6;11), А4 (6;9;3).
18. А1 (7;2;2), А2 (5;7;7), А3 (5;3;1), А4 (2;3;7).
19. А1 (8;6;4), А2 (10;5;5), А3 (5;6;8), А4 (8;10;7).
20. А1 (7;7;3), А2 (6;5;8), А3 (3;5;8), А4 (8;4;1).
21. Уравнение одной из сторон квадрата х + 3у – 5 = 0. Составить уравнения трех остальных сторон квадрата, если (-1;0) – точка пересечения его диагоналей.
22. Даны уравнения одной из сторон ромба х - 3у + 10 = 0 и одной из его диагоналей х + 4у – 4 = 0; диагонали ромба пересекаются в точке (0, 1). Найти уравнения остальных сторон ромба.
23. Уравнения двух сторон параллелограмма х + 2у + 2 = 0 и х + у = 0, а уравнение одной из его диагоналей х – 2 = 0. Найти координаты вершин параллелограмма.
24. Даны две вершины А(-3;3) и В(5;-1) и точка D(4;3) пересечения высот треугольника. Составить уравнения его сторон.
25. Даны вершины А(-3;-2), В(4;-1), С(1;3) трапеции АВСD (AD  ВС). Известно, что диагонали трапеции взаимно перпендикулярны. Найти координаты вершины D этой трапеции.
ВС). Известно, что диагонали трапеции взаимно перпендикулярны. Найти координаты вершины D этой трапеции.
26. Даны уравнения двух сторон треугольника 5х - 4у + 15 = 0 и 4х + у – 9 = 0. Его медианы пересекаются в точке (0;2). Составить уравнение третьей стороны треугольника.
27. Даны две вершины А(2;-2) и В(3;-1) и точка Р(1;0) пересечения медиан треугольника АВС. Составить уравнение высоты треугольника, проведенной через третью вершину С.
28. Даны уравнения двух высот треугольника х + у = 4 и у = 2х и одна из его вершин А(0;2). Составить уравнения сторон треугольника.
29. Даны уравнения двух медиан треугольника х - 2у + 1 = 0 и у – 1 = 0 и одна из его вершин (1;3). Составить уравнения его сторон.
30. Две стороны треугольника заданы уравнениями 5х - 2у – 8 = 0 и 3х - 2у – 8 = 0, а середина третьей стороны совпадает с началом координат. Составить уравнение этой стороны.
31. Составить уравнение линии, расстояние каждой точки которой от начала координат и от точки А(5;0) относятся как 2:1.
32. Составить уравнение линии, расстояние каждой точки которой от точки А(-1;0) вдвое меньше расстояния ее от прямой х = - 4.
33. Составить уравнение линии, расстояния каждой точки которой от точки А(2;0) и от прямой 5х + 8 = 0 относятся как 5: 4.
|
|
|
34. Составить уравнение линии, каждая точка которой находится вдвое дальше от точки А(4;0), чем от точки В(1;0).
35. Составить уравнение линии, расстояния каждой точки которой от точки А(2;0) и от прямой 2х + 5 = 0 относятся как 4: 5.
36. Составить уравнение линии, расстояние каждой точки которой от точки А(3;0) вдвое меньше расстояния от точки В(26;0).
37. Составить уравнение линии, каждая точка которой одинаково удалена от точки А(0;2) и от прямой у – 4 = 0.
38. Составить уравнение линии, каждая точка которой равноотстоит от оси ординат и от окружности х2 + у2 = 4х.
39. Составить уравнение линии, каждая точка которой равноудалена от точки А(2;6) и о прямой у + 2 = 0.
40. Составить уравнение линии, каждая точка которой отстоит от точки А(-4;0) втрое дальше, чем от начала координат.
41 – 50. Линия задана уравнением r = r(φ) в полярной системе координат. Требуется: 1) построить линию по точкам, начиная от φ = 0 до φ = 2π и придавая φ значения через промежуток π/8; 2) найти уравнение данной линии в прямоугольной декартовой ситеме координат, у которой начало координат совпадает с полюсом, а положительная полуось абсцисс – с полярной осью; 3) по полученному уравнению определить, какая это линия.
41. 
43. 
45. 
47. 
49. 
42. 
44. 
46. 
48. 
50. 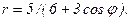
51 - 60. Дана система линейных уравнений:

Доказать ее совместность и решить двумя способами: 1) методом Гаусса; 2) средствами матричного исчисления.
51.  52.
52. 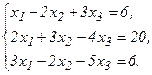
53.  54.
54. 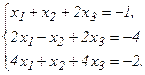
55.  56.
56. 
57.  58.
58. 
59.  60.
60. 
61 - 80. Решить систему трех уравнений с тремя неизвестными при помощи определителей.
61.  62.
62. 
63.  64.
64. 
65.  66.
66. 
67.  68.
68. 
69.  70.
70. 
71.  72.
72. 
73.  74.
74. 
75.  76.
76. 
77.  78.
78. 
79.  80.
80. 
Контрольная работа №2
81 - 90. Дано комплексное число а. Требуется:1) записать число а в алгебраической и тригонометрической формах; 2) найти все корни уравнения z3 + а = 0.
81.  . 82.
. 82.  .
.
83.  . 84.
. 84. 
85.  . 86.
. 86. 
87.  . 88.
. 88.  .
.
89.  . 90.
. 90.  .
.
91 - 95. Построить график функции у = Аsin(ax+b) преобразованием графика функции у = sin x.
91.  .
.
92.  .
.
93. 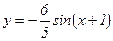 .
.
94. 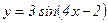 .
.
95.  .
.
96 - 100. Построить график функции y = A cos(ax+b) преобразованием графика функции y = cos x.
96.  .
.
97. 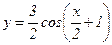 .
.
98.  .
.
99.  .
.
100.  .
.
101 - 120. Найти пределы функций, не пользуясь правилом Лопиталя.
| 101. | а) 
| б) 
|
в) 
| г) 
| |
| 102. | а) 
| б) 
|
в) 
| г) 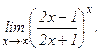
| |
| 103. | а) 
| б) 
|
в) 
| г) 
| |
| 104. | а) 
| б) 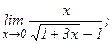
|
в) 
| г) 
| |
| 105. | а) 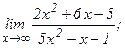
| б) 
|
в) 
| г) 
| |
| 106. | а) 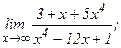
| б) 
|
в) 
| г) 
| |
| 107. | а) 
| б) 
|
в) 
| г) 
| |
| 108. | а) 
| б) 
|
в) 
| г) 
| |
| 109. | а) 
| б) 
|
в) 
| г) 
| |
| 110. | а) 
| б) 
|
в) 
| г) 
| |
| 111. | а) 
| б) 
|
в) 
| г) 
| |
| 112. | а) 
| б) 
|
в) 
| г) 
| |
| 113. | а) 
| б) 
|
в) 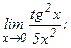
| г) 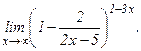
| |
| 114. | а) 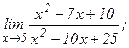
| б) 
|
в) 
| г) 
| |
| 115. | а) 
| б) 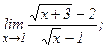
|
в) 
| г) 
| |
| 116. | а) 
| б) 
|
в) 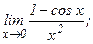
| г) 
| |
| 117. | а) 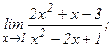
| б) 
|
в) 
| г) 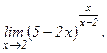
| |
| 118. | а) 
| б) 
|
в) 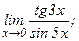
| г) 
| |
| 119. | а) 
| б) 
|
в) 
| г) 
| |
| 120. | а) 
| б) 
|
в) 
| г) 
|
|
|
|
121 - 130. Задана функция y = f(x) и два значения аргумента х1 и х2. Требуется: 1) установить, является ли данная функция непрерывной или разрывной для каждого из данных значений аргумента; 2) в случае разрыва функции найти ее пределы в точке разрыва слева и справа; 3) сделать схематический чертеж.
121. f(x)=91/(2-x), x1=0, x2=2.
123. f(x)=121/x, x1=0, x2=2.
125. f(x)=81/(5-x), x1=3, x2=5.
127. f(x)=141/(6-x), x1=4, x2=6.
129. f(x)=111/(4+x), x1=-4, x2=-2.
122. f(x)=41/(3-x), x1=1, x2=3.
124. f(x)=31/(4-x), x1=2, x2=4.
126. f(x)=101/(7-x), x1=5, x2=7.
128. f(x)=151/(8-x), x1=6, x2=8.
130. f(x)=131/(5+x), x1=-5, x2=-3.
В задачах 131 - 140 даны функции y = f(x) и значения аргумента х1 и х2. Требуется: 1) установить, является ли данная функция непрерывной или разрывной при данных значениях аргумента; 2) найти односторонние пределы в точках разрыва; 3)построить график данной функции.
131. 
133. 
135. 
137. 
139. 
132. 
134 
136. 
138. 
140. 
В задачах 141 - 150 функция у задана различными аналитическими выражениями для различных областей изменения аргумента х. Требуется: 1) найти точки разрыва функции, если они существуют; 2) найти односторонние пределы и скачок функции в точках разрыва; 3) сделать чертеж.
| 141. | 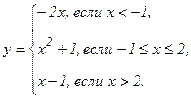
| 146. | 
|
| 142. | 
| 147. | 
|
| 143. | 
| 148. | 
|
| 144. | 
| 149. | 
|
| 145. | 
| 150. | 
|
151 - 160. Задана функция y = f(x). Найти точки разрыва функции, если они существуют. Сделать чертеж.
151. 

152. 

153. 

154. 

155. 

156. 

157. 

158. 

159. 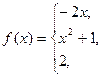
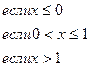
160. 

Контрольная работа №3
161 - 170. Найти производные  данных функций.
данных функций.
| 161. | 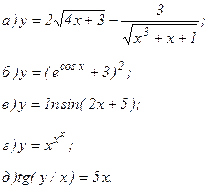
| 162. | 
|
| 163. | 
| 164. | 
|
| 165. | 
| 166. | 
|
| 167. | 
| 168. | 
|
| 169. | 
| 170. | 
|
171 - 180. Найти  и
и 
171. 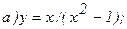

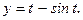
172. 


173. 


174. 
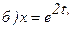

175. 


176. 

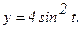
177. 

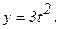
178. 
 ,
, 
179. 
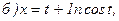

180. 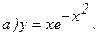

 .
.
181 - 190. Найти наибольшее и наименьшее значения функции у = f(x) на отрезке 
181. 
182. 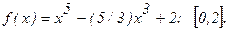
183. 
184. 
185. 
186. 
187. 
188. 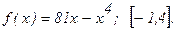
189. 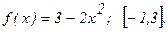
190. 
191 - 210. Исследовать методами дифференциального исчисления функцию и, используя результаты исследования, построить ее график.
191. у = 4х/(4+х2) 192. y = (x2-1)/(x2 +1)
193. y = (x2+1)/(x2-1) 194. y = x2/(x-1)
195. y = x3/(x2+1) 196. y = (4x3+5)/x
197. y = (x2-5)/(x-3) 198. y = x4/(x3-1)
199. y = 4x3/(x3-1) 200. y = (2-4x2)/(1-4x2)
201. y = (1nx)/ 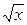 202. y = x
202. y = x 
203. y =  204. y = x2-21nx
204. y = x2-21nx
205. y = 1n (x2-4) 206. y = e1/(2-x)
207. y = 1n (x2+1) 208. y = (2+x2) 
209. y = 1n (9-x2) 210. y = (x-1)e3x+1.
211. Дана функция z = y/(x2- y2)5. Показать, что 
212. Дана функция z = y2/(3x)+arcsin(xy). Показать, что 
213. Дана функция z = 1n(x2+y2+2x+1). Показать, что 
214. Дана функция z = exy. Показать, что 
215. Дана функция z = 1n(x+e-y). Показать, что 
216. Дана функция z = x/y. Показать, что 
217. Дана функция z = xy. Показать, что 
218. Дана функция z = xey/x. Показать, что 
219. Дана функция z = sin(x+ay). Показать, что 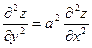
220. Дана функция z = cosy+(y - x)siny. Показать, что 
221 - 230. Дана функция z = f(x,y) и две точки А (х0, у0) и В (х1, у1). Требуется: вычислить значение z1 функции в точке В; 2) вычислить приближенное значение  функции в точке В, исходя из значения z0 функции в точке А, заменив приращение функции при переходе от точки А к точке В дифференциалом, и оценить в процентах относительную погрешность, возникающую при замене приращения функции ее дифференциалом; 3) составить уравнение касательной плоскости к поверхности z = f(x,y) в точке С (х0, у0, z0).
функции в точке В, исходя из значения z0 функции в точке А, заменив приращение функции при переходе от точки А к точке В дифференциалом, и оценить в процентах относительную погрешность, возникающую при замене приращения функции ее дифференциалом; 3) составить уравнение касательной плоскости к поверхности z = f(x,y) в точке С (х0, у0, z0).
221. z = x2+xy+y2; А (1;2), В (1,02;96)
222. z = 3x2-xy+x+y; А (1;3), В (1,06;2,92)
223. z = x2+3xy-6y; А (4;1), В (3,96;1,03)
224. z = x2-y2+6x+3y; А (2;3), В (2,02;2,97)
225. z = x2+2xy+3y2; А (2;1), В (1,96;1,04)
226. z = x2+y2+2x+y-1; А (2;4), В (1,98;3,91)
227. z = 3x2+2y2-xy; А (-1;3), В (-0,98;2,97)
228. z = x2-y2+5x+4y; А (3;3), В (3,02;2,98)
229. z = 2xy+3y2-5x; А (3;4), В (3,04;3,95)
230. z = xy+2y2-2x; А (1;2), В (0,97;2,03).
231 - 240. Найти наименьшее и наибольшее значения функции z = f(x,y) в замкнутой области D, заданной системой неравенств. Сделать чертеж.
231. z = x2+y2-9xy+27; 
 .
.
232. z = x2+2y2+1; 
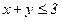 .
.
233. z = 3-2x2-xy-y2; 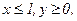
 .
.
234. z = x2+3y2+x-y; 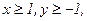
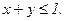
235. z = x2+2xy+2y2; 
 .
.
236. z = 5x2-3xy+y2+4; 
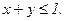
237. z = 10+2xy-x2; 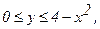
238. z = x2+2xy-y2+4x; 
 .
.
239. z = x2+xy-2; 
240. z = x2+xy; 
 .
.
241 - 250. Даны функции z = z(x,y), точка А (х0,у0) и вектор а. Найти; 1) grad z в точке А; 2)производную в точке А по направлению вектора а.
241. z = x2+xy+y2; А (1;1), а = 2 i - j.
242. z = 2x2+3xy+y2; А (2;1), a = 3i-4 j.
243. z = 1n(5x2+3y2); А (1;1), a = 3i+2 j.
244. z = 1n(5x2+4y2); А (1;1), a = 2 i - j.
245. z = 5x2+6xy; А (2;1), a = i +2 j.
246. z = arctg(xy2); А (2;3), a = 4 i -3 j.
247. z = arcsin (x2/y); А (1;2), a = 5 i -12 j.
248. z = 1n(3x2+4y2); А (1;3), a = 2 i - j.
249. z = 3x4+2x2y3; А (-1;2), a = 4 i -3 j.
250. z = 3x2y2+5y2x; А (1;1), a = 2 i + j.
251 - 260. Экспериментально получены пять значений искомой функции y = f(x) при пяти значениях аргумента, которые записаны в таблице. Методом наименьших квадратов найти функцию y = f(x) в виде у = ах + b.
251.
| х | |||||
| у | 4,3 | 5,3 | 3,8 | 1,8 | 2,3 |
252.
| х | |||||
| у | 4,5 | 5,5 | 4,0 | 2,0 | 2,5 |
253.
| х | |||||
| у | 4,7 | 5,7 | 4,2 | 2,2 | 2,7 |
254.
| х | |||||
| у | 4,9 | 5,9 | 4,4 | 2,4 | 2,9 |
255.
| х | |||||
| у | 5,1 | 6,1 | 4,6 | 2,6 | 3,1 |
256.
| х | |||||
| у | 3,9 | 4,9 | 3,4 | 1,4 | 1,9 |
257.
| х | |||||
| у | 5,2 | 6,2 | 4,7 | 2,7 | 3,2 |
258.
| х | |||||
| у | 5,5 | 6,5 | 5,0 | 3,0 | 3,5 |
259.
| х | |||||
| у | |||||
|
|
|


