 |
Теория вероятностей и математическая статистика
|
|
|
|
Нормальным называют распределение вероятностей непрерывной случайной величины Х, плотность которого имеет вид
где а – математическое ожидание, σ – среднее квадратическое отклонение Х.
Вероятность того, что Х примет значение, принадлежащее интервалу (α,β),
Р(α<х<β)=Ф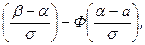 
(1)
где Ф(х)=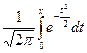 
- функция Лапласа.
Пример 1. Математическое ожидание а нормально распределенной случайной величины Х а=10, среднее квадратическое отклонение σ= 2. Найти вероятность попадания этой величины в интервал (12;14).
Решение: Подставив в формулу (1) α=12, β=14, а=10, σ=2, получаем
Р(12<х<14)=Ф 
По таблице для функции Лапласа находим, что Ф(2)= 0,4772, Ф(1)=0,3413 и искомая вероятность Р(12<х<14)=0,1359.
Оценки, которые определяются одним числом, называют точечными. При малом числе наблюдений эти оценки могут приводить к грубым ошибкам. Чтобы избежать этих ошибок, используют интервальные оценки, которые определяются двумя числами – концами интервала (в котором заключена оцениваемая величина с заданной вероятностью).
Таким образом, задача сводится к отысканию такого интервала (его называют доверительным), который с заданной вероятностью γ (ее называют надежностью) покрывают оцениваемый параметр. Наиболее часто надежность принимают равной 0,95 или 0,99, или 0,999.
В частности, при надежности γ=0,95 доверительный интервал для оценки математического ожидания а нормального распределения (по выборочной средней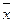 
выборки объема n, при известном σ) находят по формуле
В обозначениях формула принимает вид: 
Если доверительный интервал найден, то с надежностью 0,95 можно считать, что оцениваемый параметр заключен в этом интервале.
Пример 2. Найти доверительный интервал для оценки математического ожидания а нормального распределения с надежностью 0,95, зная выборочную среднюю 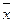=10,43 (статистическую среднюю 
), объем выборки (число наблюдений) n=100 и среднее квадратическое отклонение σ=5.
|
|
|
Решение: Воспользуемся формулой:
Подставляя данные, получаем:
10,43-1,96(5/10)< а <10,43+1,96(5/10), или окончательно 9,45< а <11,41.
Контрольные задания
Ниже приведена таблица номеров задач, входящих в задания на контрольные работы.
Студент выполняет тот вариант контрольных работ, который совпадает с последней цифрой его учебного шифра. При этом если предпоследняя цифра учебного шифра есть число нечетное (1, 3, 5, 7, 9), то номера задач для соответствующего варианта даны в табл. 1; если же предпоследняя цифра учебного шифра есть число четное или ноль (2, 4, 6, 8, 0), то номера задач для соответствующего варианта даны в табл.2
Таблица 1
| № в-та | Номера задач для контрольных работ на первом курсе | ||||||||||||||||||||||||||||||||||||
| Работа 1 | Работа 2 | Работа 3 | |||||||||||||||||||||||||||||||||||
| № в-та | Номера задач для контрольных работ на втором курсе | ||||||||||||||||||||||||||||||||||||
| Работа 4 | Работа 5 | Работа 6 | |||||||||||||||||||||||||||||||||||
Таблица 2
|
|
|
| № в-та | Номера задач для контрольных работ на первом курсе | |||||||||||||||||||||||||
| Работа 1 | Работа 2 | Работа 3 | ||||||||||||||||||||||||
| № в-та | Номера задач для контрольных работ на втором курсе | |||||||||||||||||||||||||
| Работа 4 | Работа 5 | Работа 6 | ||||||||||||||||||||||||
|
|
|
ЛИТЕРАТУРА
1. Клетеник Д.В. «Сборник задач по аналитической геометрии» - М., Гостехиздат, 1954-1956 гг.; М., Физматгиз, 1958-1963 гг.; М., Наука, 1965-1980 гг.
2. Пискунов Н.С. «Дифференциальное и интегральное исчисления для вузов» - М., Наука, 1970-1978 гг., т. 1, 2.
3. «Задачи и упражнения по математическому анализу для вузов» / Под ред. Б.П. Демидовича – М., Физматгиз, 1959-1963 гг.; М., Наука, 1964-1978 гг.
4. Моисеенко А.М., Александрова Е.В. «Линейная алгебра».
5. Уварова М.Н., Александрова Е.В. «Теория вероятности».
|
|
|
