IV. Функции нескольких переменных

 

Частной производной от функции z = f(x; у) по независимой переменной х называется конечный предел

вычисленный при постоянном у.

Частной производной по у называется конечный предел

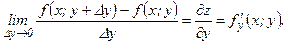
вычисленный при постоянном х.

Для частных производных справедливы обычные правила и формулы дифференцирования.

Частными производными второго порядка от функции z = f(x; у), называются частные производные от ее частных производных первого порядка.

Обозначение частных производных второго порядка:

Так называемые «смешанные» производные , отличающиеся друг от друга лишь последовательностью дифференцирования, равны между собой, если они непрерывны:

Пример 1. Дана функция z = yln (x² – y²). Показать, что:

(1)

Решение.

Рассматривая у как постоянную величину, находим: Рассматривая х как постоянную величину, находим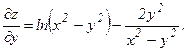

Подставим найденные частные производные в левую часть равенства (1):

Получаем тождество, т.е. функция z удовлетворяет данному уравнению (1).

 

 

Пример 2. Для функции z = xy² = sin (x + y) найти все частные производные второго порядка.

Решение.

Найдем сначала частные производные первого порядка:

 

Найдем теперь частные производные второго порядка:

 

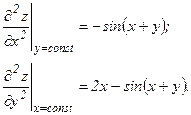
Смешанные» частные производные второго порядка:

Пример 3. Дана функция z = x² + y² - 3xy и две точки А(х₀; у₀) и В(х₁; у₁), где А(1; 3) и В(1,02; 2,97). Требуется:

1) вычислить значение z₁ функция в точке В;

2) вычислить приближенное значение функции в точке В, исходя из значения z₀ функции в точке А, заменив приращение функции при переходе от точки А к точке В дифференциалом, и оценить в процентах относительную погрешность, возникающую при замене приращения функции ее дифференциалом;

3) составить уравнение касательной плоскости к поверхности z = f(x; у) в точке С(х₀, у₀, z₀).

 

Решение.

1) Подставим значение х₁ =1,02 и у₁ =2,97 в данное уравнение, получим аппликату z₁ точки В: z₁ = (1,02)²+ (2,97)² – 3^.1,02^.2,97 = 0,7731.

2) Подставим значение х₀ = 1, у₀ = 3 в данное уравнение, получим значение функции z₀ в точке А: z₀ =1²+3²-3^.1^.3=1 + 9 – 9 = 1.

Полный дифференциал функции z = f(x; у), вычисляется по формуле

При достаточно малом для дифференцируемой функции z = f(x; у) справедливы приближенные равенства:

∆z ≈ dz; f(x + ∆х; у + ∆у) ≈ f (x; у) + dz.

В данном примере требуется вычислить z (1,02; 2,97) ≈ z (1; 3) + dz = z₀+ dz = 1 + dz.

Найдем приращение функции ∆z при ∆х = 0,02, ∆у = -0,03;

Найдем частные производные функции z = x² + y² - 3xy:

Для точки А, где х =1, у =3, получаем: dz = (2x –3y)∆x + (2y – 3x)∆y = (2 – 9)(0,02) + (6 – 3) = -0,14 – 0,09 = -0,23. Следовательно, z (1,02; 2,97) ≈ 1 – 0,23 = 0,77 и таким образом 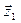≈ 0,77, z₁ = 0,7731 в точке В.

Относительной погрешностью приближенного значения 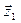числа z₁ называется отношение абсолютной погрешности к модулю приближенного значения, т.е.:

Таким образом:

.

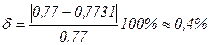Пример 4. При исследовании функции нескольких переменных на экстремум следует иметь в виду, что точки экстремума могут находиться как среди точек, в которых частные производные равны нулю, так и среди точек, в которых частные производные не существуют. Например, функция z = имеет минимум в точке (0; 0), тогда как в этой точке ее частные производные не существуют. При отыскании наибольшего и наименьшего значений функции в некоторой замкнутой области следует найти все внутренние точки области, в которых функция может иметь экстремум. Затем надо исследовать функцию на границе области и найти там точки, где функция может принимать наименьшие (наибольшие) значения. При этом часто приходится разбивать границу области на части, заданные различными уравнениями. Вычислив значения функции во всех найденных точках, следует сравнить их между собой: наибольшее (наименьшее) из этих значений и является наибольшим (наименьшим) значением функции во всей замкнутой области.

 

Рассмотрим пример: требуется найти наибольшее и наименьшее значение функции z = 2x³ – 6xy + 3y³ в замкнутой области, ограниченной осью Оу, прямой у = 2 и параболой у = х²/2 при х ≥ 0.

Решение.

Точки, в которых функция принимает наибольшее и наименьшее значения, могут находится, как внутри области, так и на ее границе. Если функция принимает наибольшее (наименьшее) значение внутренней точке области, то в этой точке частные производные равны нулю. Решив систему уравнений

найдем две точки О(0; 0) и М(1; 1), в которых обе частные производные равны нулю. Первая из них принадлежит границе области. Следовательно, если функция z принимает наибольшее (наименьшее) значение во внутренней точке области, то это может быть только в точке М(1; 1). Исследуем функцию на границе области.

На отрезке ОА имеем х = 0, поэтому на этом отрезке z = 3y² (0 ≤ у ≤ 2) – возрастающая функция одной переменной у; наибольшее и наименьшее значения она принимает на концах отрезка ОА.

На отрезке АВ имеем у = 2, следовательно, на этом отрезке функция z = 2x³ – 6x^.2 + 3^.2² = 2x³ – - 12x + 12 (0 ≤ x ≤2) представляет собой функцию одной переменной х, ее наибольшее и наименьшее значения среди ее значений в критических точках и на концах отрезка. Находим производную 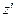= 6 х ² – 12. Решая уравнение 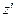= 0 или 6 х² – 12 = 0, находим Внутри отрезка 0 ≤ х ≤ 2 имеется лишь одна критическая точка 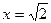; соответствующей точкой отрезка АВ является точка Q(). Итак, наибольшее и наименьшее значения функции z на отрезке АВ находятся среди ее значений в точках А, Q и В.

На дуге ОВ параболы у = х²/2 имеем z = 2x³ – 6x (x²/2) + 3 (x²/2)² = (3/4) x⁴ – x³ (0 ≤ x ≤ 2).

Решаем уравнение 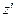= 3 х³ –3 х² = 0 или х² (х – 1) = 0 и находим его корни: х₁ =0 и х₂ =1. Таким образом, наибольшее и наименьшее значения функции z на дуге ОВ находятся среди ее значений в точках О, Р и В.

Следовательно, наибольшее и наименьшее значения функции z = 2x³ – 6xy + 3y² в данной замкнутой области находятся среди ее значений в точках О, А, Q, В, Р, М, т.е. среди значений z (0) = z (0; 0) = 0; z (A) = z (0; 2) = 12; z (Q) = z () = 12 – 8 ; z (В) = z (2; 2) = 4; z (P) = z (1; 1/2) = -1/4; z (M) = z (1; 1) = -1.

Наибольшее и наименьшее из них равны соответственно 12 и –1.

Они являются наибольшим и наименьшим значениями данной функции в данной замкнутой области: z_наиб = 12, z_наим = -1.

 

Пример 5. Дана функция z = ln (x² + y²), точка А(3; 4) и вектор

 

Найти: 1) в точке А;

2)производную в точке А по направлению вектора

Решение.

Градиентом функции z = f(x,y) в точке А(х₀; у₀) называется вектор с началом в точке А, имеющий своими координатами частные производные функции z в точке А.

1) Найдем значение частных производных функции z в точке А:

 

Следовательно,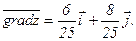

2) Производная дифференцируемой функции z = f(x, у) в точке А(х₀, у₀) по направлению вектора вычисляется по формуле

где α – угол, образованный вектором с осью Ох.

Градиент функции и производная в направлении вектора связаны формулой:

Проекция вектора на вектор равен скалярному произведению этих векторов, деленному на модуль вектора .

где

Тогда производная функции z в точке А по направлению вектора

Пример 6. Экспериментально получены 5 значений искомой функции z = f(x) при пяти значениях аргумента, которые записаны в таблице. Методом наименьших квадратов найти функцию у = f(x) в виде у = ах + в.

 

х
у	3,5	4,4	3,2	1,8	2,4

 

Решение.

Чаще всего при подборе эмпирических формул пользуются так называемым принципом наименьших квадратов. Он основан на том, что из данного множества формул вида у = f(x) наилучшим образом изображающим данные значения считается то, для которой сумма квадратов отклонений наблюдаемых значений от вычисленных является наименьшей.

Подбор параметров функции f(x) после того, как вид функции у = f(x) определен, называют методом наименьших квадратов.

Линейной функции у = ах + в нужно подбирать коэффициенты а и в таким образом, чтобы сумма квадратов отклонений вычисленных значений ах_i + в от наблюдаемых значений у_i, т.е. величина S = (ax₁ + в – у₁)² + (ах₂ + в –у₂)² + …+(ах_к + в –у_к)², принимает наименьшее значение. Сумма является функцией двух переменных а и в, а поэтому она принимает минимальное значение при тех значениях а и в, при которых обращаются в нуль частные производные этой функции по каждой переменной, т.е. когда

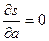и .

Находим частные производные:

 

 

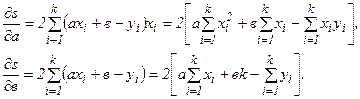
Приравнивая каждую частную производную нулю, получаем систему линейных уравнений относительно а и в, так называемую нормальную систему:

 

(1)

 

Для составления системы нормальных уравнений (1) составим таблицу подсчетов, произведя все необходимые вычисления:

 

х						15=1+2+3+4+5
у	3,5	4,4	3,2	1,8	2,4	15,3=3,5+4,4+3,2+1,8+2,4
х2						55=1+4+9+16+25
ху	3,5	8,8	9,6	7,2		41,1=3,5+8,8+9,6+7,2+12
	∑

 

Получим данные для составления системы

Решим систему по формулам Крамера.

 

Главный определитель системы 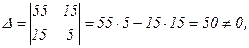следовательно система имеет единственное решение, вычисляем побочные определители системы:

 

Таким образом,

 

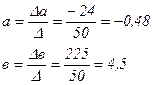
Искомая зависимость между х и у выражается так: у = -0,48 х + 4,5.

 

⇐ Предыдущая12345678Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: