 |
Элементы теории вероятности
|
|
|
|
Вероятностью события А называют отношение числа благоприятствующих этому событию исходов к общему числу всех равновозможных несовместных элементарных исходов, образующих полную группу:
 (2.1)
(2.1)
P(A) - вероятность события, m – число элементарных исходов благоприятствующих А, n – число всех возможных элементарных исходов.
Пример 1
Набирая номер телефона, абонент забыл одну цифру и набрал её наудачу. Найти вероятность того, что набрана нужная цифра.
Решение:
Обозначим через А событие – набрана нужная цифра. Абонент мог набрать любую из 10 цифр, поэтому общее число возможных элементарных исходов равно 10. Эти исходы несовместны, равновозможны и образуют полную группу. Благоприятствует событию А лишь один исход(нужная цифра лишь одна). Искомая вероятность равна отношению числа исходов, благоприятствующих событию, к числу всех элементарных исходов:
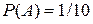 (2.2)
(2.2)
Формулы комбинаторики
Перестановками называют комбинации, состоящие из одних и тех же n различных элементов и отличающиеся только порядком их расположения. Число всех возможных перестановок
 , (2.3)
, (2.3)
где  ,
, 
Пример 2
Сколько трёхзначных чисел можно составить из цифр 1, 2, 3, если каждая цифра входит в изображение числа только один раз?
Решение: Искомое число трёхзначных чисел
 .
.
Размещениями называют комбинации, составленные из n различных элементов по m элементов, которые отличаются либо составом элементов, либо их порядком. Число всех возможных размещений
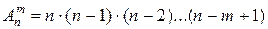 (2.4)
(2.4)
Пример 3
Сколько можно составить сигналов из 6 флажков различного цвета, взятых по 2?
Решение. Искомое число сигналов
 . (2.5)
. (2.5)
Сочетаниями называют комбинации, составленные из n различных элементов по m элементов, которые хотя бы одним элементом. Число сочетаний
|
|
|
 (2.6)
(2.6)
Пример 4. Сколькими способами можно выбрать две детали из ящика, содержащего 10 деталей?
Решение. Искомое число способов
 (2.7)
(2.7)
Числа размещений, перестановок и сочетаний связаны равенством
 (2.8)
(2.8)
Случайная величина
Случайной называют величину, которая в результате испытания примет одно и только одно возможное значение, наперёд неизвестное и зависящее от случайных причин, которые заранее не могут быть учтены.
Случайные величины могут быть дискретными и непрерывными
Дискретной (прерывной) называют случайную величину, которая принимает отдельные, изолированные возможные значения с определёнными вероятностями. Число возможных значений дискретной случайной величины может быть конечным или бесконечным.
Непрерывной называют случайную величину, которая может принимать все значения из некоторого конечного или бесконечного промежутка. Очевидно, число возможных значений непрерывной случайной величины бесконечно.
Законом распределения дискретной случайной величины называют соответствие между возможными значениями и их вероятностями; его можно задать таблично, аналитически (в виде формулы) и графически.
Принято обозначать сами случайные величины прописными буквами X, Y, Z, а их возможные значения – соответствующими строчными буквами x, y, z.
Пример 1
В денежной лотерее выпущено 100 билетов. Разыгрывается один выигрыш в 50 рублей и десять выигрышей по 1 рублю. Найти закон распределения случайной величины Х – стоимости возможного выигрыша для владельца одного лотерейного билета.
Решение: Напишем возможные значения Х:  Вероятности этих возможных значений таковы:
Вероятности этих возможных значений таковы:  .
.
Напишем закон распределения:
Х 50 10 0
р 0.01 0.1 0.89
Контроль: 0.01 + 0.1 + 0.89 = 1 Суммарная вероятность не должна превышать единицу).
Математическим ожиданием дискретной случайной величины называют сумму произведений всех её возможных значений на их вероятности:
|
|
|
 (2.9)
(2.9)
Пример 2
Найти математическое ожидание случайной величины Х, зная закон её распределения:
Х 3 5 2
Р 0.1 0.6 0.3
Решение: искомое математическое ожидание равно сумме произведений всех возможных значений случайной величины на их вероятности.

|
|
|


