 |
I . Первичные оценки по шкале оценки потребности в достижениях.
|
|
|
|
1) Статистические ряды - n *
Совпадение с ключом - Х
а) Вариационный ряд учителя №1
n* 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22
Х 1 1 1 1 1 1 1 1 1 1 1 1 1
б) Вариационный ряд учителя №2
n* 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22
X 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
в) Вариационный ряд учителя №З
n* 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22
X 1 1 1 1 1 1 1 1 1 1 1
г) Вариационный ряд учителя №4
n* 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22
X 1 1 1 1 1 1 1 1 1 1
2.Первичные оценки по Т. Элерсу.
1) Статистические ряды - п *
Тестовый показатель - Y
а) Вариационный ряд учителя №1
n* 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22
Y 1 1 1 1 1
n* 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41
Y 1 1 1 1 1 1 1 1 1 1 1
б) Вариационный ряд учителя №2
n* 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22
Y 1 1 1 1 1 1 1 1
n* 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34. 35, 36, 37, 38, 39, 40, 41
Y 1 1 1 1 1 1 1 1 1 1 1 1 1
в) Вариационный ряд учителя №3
n* 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22
Y 1 1 1 1 1
n* 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41
Y 1 1 1 1 1 1 1 1
г) Вариационный ряд учителя №4
n* 1, 2, 3, 4, 5, 6, 7, 8, 9,10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22
Y 1 1 1
n* 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34,35,36,37,38,39, 40, 41
Y 1 1 1 1 1 1
Одним из основных принципов определения количественных критериев корреляционной связи коэффициентов корреляции — является сравнение величин отклонений от среднего значения по каждой группе в сопряженных парах сравниваемых рядов переменных. С целью достижения независимости меря корреляционной связи от числа сравниваемых пар и величин стандартных отклонений в сопоставимых рядах. мера носит название коэффициента корреляции — произведение моментов Пирсона (г) (см. ниже), где X1 и У1 - сравниваемые количественные признаки, n — число сравниваемых наблюдений,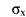 
а 
и - стандартные отклонения в сопоставимых рядах. Определение статистической зависимости коэффициента rxy проводится с помощью критерия Стьюдента (t)(формулы приведены ниже).
|
|
|
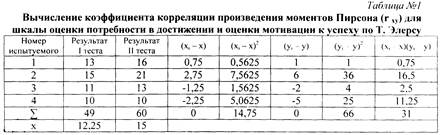
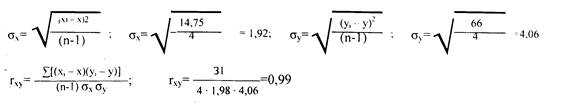
Коэффициент детерминации г²xy, выражающий степень вариации переменных, равен г²xy =0.98. что свидетельствует о том, что 98% измерений признаков объясняются их совместным распределением (взаимовлиянием).
Определение статической зависимости коэффициента гxy, с помощью критерия Стьюдента (t):
Вывод: по нашей шкале различия значимы на уровне р ≤ 0,01. Нулевая гипотеза отвергается и принимается гипотеза о различии.
Коэффициент детерминации г²xy выражающий степень вариации переменных, равен г²xy = 0.88, что свидетельствует о том, что 88% измерений признаков объясняются их совместным распределением (взаимовлиянием).
Определение статической зависимости коэффициента гxy с помощью критерия Стьюдента (t):
Степень свободы п'=2
0,05; 0,01; 0,1 — процент вероятности нулевых гипотез.
По таблице распределения Стьюдента для п’=2 находим:
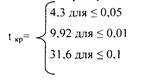
Вывод: t эмпирическое попало в зону незначимости, t эм < t кр, гипотеза о различии отклоняется, принимается гипотеза о сходстве.
Коэффициент детерминации г²xy, выражающий степень вариации переменных. равен г²xy =0,08, что свидетельствует о том, что только 8% измерений признаков объясняются их совместным распределением (взаимовлиянием).
Определение статической зависимости коэффициента с помощью критерия Стьюдента (t):
Степень свободы п’=2
0,05: 0,01; 0,1 — процент вероятности нулевых гипотез.
По таблице распределения Стьюдента для п’=2 находим:
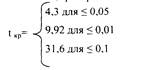
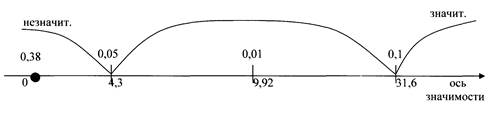
Вывод: t эмпирическое попало в зону незначимости, t эм < t кр, гипотеза о различии отклоняется, принимается гипотеза о сходстве.
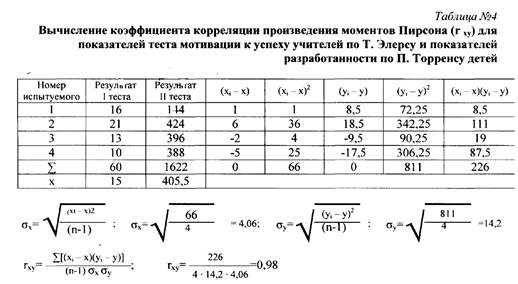
Коэффициент детерминации r²xy, выражающий степень вариации переменных, равен r²xy= 0,96, что свидетельствует о том, что 96% измерений признаков объясняются их совместным распределением (взаимовлиянием).
|
|
|
Определение статической зависимости коэффициента rxy с помощью критерия Стьюдента (t):
Степень свободы n’=2
0,05; 0,01 0,1 — процент вероятности нулевых гипотез.
По таблице распределения Стьюдента для п'=2 находим:
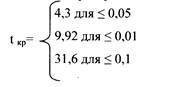
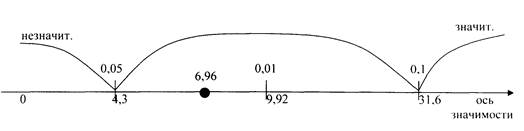
Вывод: по нашей шкале различия значимы на уровне р ≤ 0,05. Нулевая гипотеза отвергается и принимается гипотеза о различии.
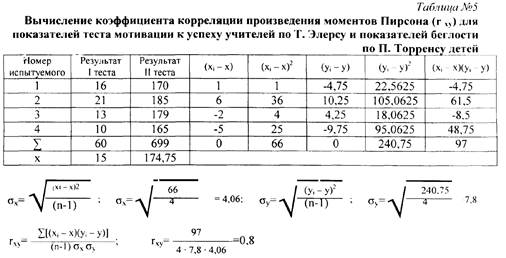
Коэффициент детерминации rxy, выражающий степень вариации переменных. равен rxy =0.64, что свидетельствует о том, что 64% измерений признаков объясняются их совместным распределением (взаимовлиянием).
Определение статической зависимости коэффициента г, с помощью критерия Стьюдента(t):
Степень свободы п'=2
0,05; 0,01; 0,1 — процент вероятности нулевых гипотез.
По таблице распределения Стьюдента для п'=2 находим:
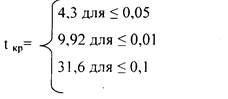
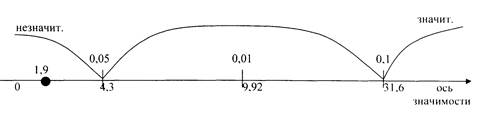
Вывод: t эмпирическое попало в зону незначимости, t эм < t кр, гипотеза о различии отклоняется, принимается гипотеза о сходстве.
ВЫВОД: корреляционный анализ привел нас к выводу, что различия незначительны, следовательно, изучаемая величина распределяется нормально. Распределение можно рассматривать как репрезентативное по отношению к генеральной совокупности. Таким образом, расхождения между характеристиками эмпирического и теоретического распределения невелики, что является подтверждением исходной гипотезы. Однако для получения более достоверных результатов для устранения различий
необходимо увеличить выборку.
|
|
|
