1.4. Преобразование детерминированного сигнала в линейных системах

 

Чтобы преобразовать входной сигнал в удобную для хранения, воспроизведения и управления форму, необходимо обосновать требования к параметрам систем преобразования сигнала. Для этого надо математически описать связь между сигналами на входе, выходе системы и параметрами системы.

В общем случае система преобразования сигнала является нелинейной: при вхождении в нее гармонического сигнала на выходе системы возникают гармоники других частот. Параметры нелинейной системы преобразования зависят от параметров входного сигнала. Общей теории нелинейности не существует [9]. Одним из способов описать связь между входным E_вх(t) и выходным E_вых(t) сигналами и параметром K нелинейности системы преобразования является следующий:

 

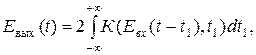
(1. 19)

 

где t и t₁ – аргументы в пространстве выходного и входного сигналов соответственно.

Нелинейность системы преобразования определяется видом функции K.

Чтобы упростить анализ процесса преобразований сигнала, используют допущение о линейности систем преобразований. Это допущение применимо к нелинейным системам, если сигнал имеет малую амплитуду гармоник, либо когда систему можно рассматривать как совокупность линейного и нелинейного звеньев. Примером такой нелинейной системы являются светочувствительные материалы (подробный анализ их преобразующих свойств будет сделан ниже).

Рассмотрим преобразование сигнала в линейных системах. Система называется линейной, если ее реакция на одновременное воздействие нескольких сигналов равна сумме реакций, вызываемых каждым сигналом, действующим отдельно [5], т. е. выполняется принцип суперпозиции [6]:

 

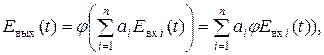
(1. 20)

 

где φ – математический оператор, показывающий, каким образом система преобразует входные сигналы в выходные;

E_вых(t) – сигнал на выходе системы преобразования;

E_{вх i}(t) – i-тая составляющая сигнала на входе системы;

a_i – постоянный сомножитель i-той составляющей сигнала.

 

 

Примером линейных систем могут служить оптические системы. Если система линейна, то связь между входным и выходным сигналом имеет конкретный вид, называемый интегралом суперпозиции:

 

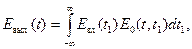
(1. 21)

 

где t, t₁ – аргументы в пространстве выходного и входного сигналов соответственно;

E₀(t, t₁) – импульсная реакция системы.

Импульсной реакцией системы называется выходной сигнал, если на вход подан сигнал, описываемый дельта-функцией Дирака. Эту функцию δ (x) определяют тремя условиями:

 

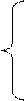
	δ (t) = 0 при t ≠ 0;	(1. 22)
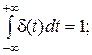
		(1. 23)
	δ (t) = δ (–t).	(1. 24)

 

Геометрически она совпадает с положительной частью вертикальной оси координат, т. е. имеет вид луча, выходящего вверх из начала координат. Физической реализацией дельта-функции Дирака в пространстве является точка с бесконечной яркостью, во времени – бесконечно короткий импульс бесконечно большой интенсивности, в спектральном пространстве – бесконечно сильное монохроматическое излучение.

Дельта-функция Дирака обладает следующими свойствами:

 

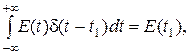
		(1. 25)
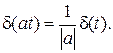
		(1. 26)

 

Если импульс происходит не на нулевом отсчете, а при значении аргумента t₁, то такую " сдвинутую" на t₁ дельта-функцию можно описать как δ (t–t₁).

Чтобы упростить выражение (1. 21), связывающее выходной и входной сигналы линейной системы, принимают допущение о нечувствительности (инвариантности) линейной системы к сдвигу. Линейная система называется нечувствительной к сдвигу, если при сдвиге импульса импульсная реакция изменяет только свое положение, но не изменяет своей формы [6], т. е. удовлетворяет равенству:

 

E0(t, t1) = E0(t – t1).

(1. 27)

 

 

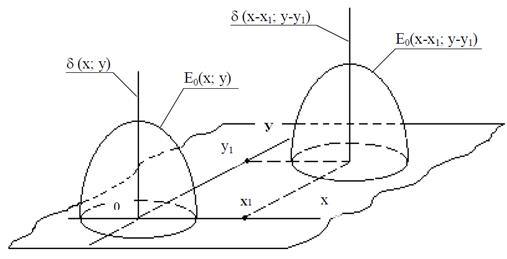
Рис. 1. 6. Нечувствительность импульсной реакции систем

или фильтров к сдвигу

 

Оптические системы, являясь линейными, чувствительны к сдвигу (не инвариантны): распределение, освещенность и размер " кружка" (в общем случае не являющегося кругом) рассеяния зависят от координаты в плоскости изображения. Как правило, в центре поля зрения диаметр " кружка" меньше, а максимальное значение импульсной реакции больше, чем по краям (рис. 1. 7).

 

 

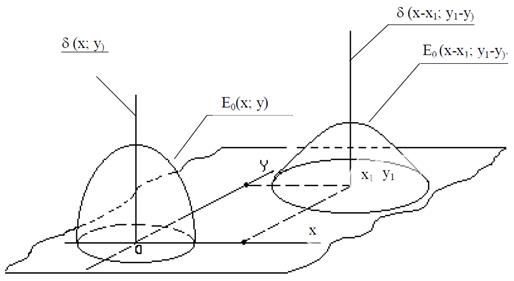
Рис. 1. 7. Чувствительность импульсной реакции к сдвигу

Для нечувствительных к сдвигу линейных систем выражение (1. 21), связывающее входной и выходной сигналы, приобретает более простой вид:

 

.

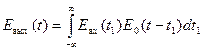(1. 28)

 

Указанное выражение представляет свертку функций E_вх(t) и E₀(t). Свертка – это операция получения функции f(t) из функций f₁(t) и f₂(t), имеющая вид:

 

(1. 29)

 

Из определения свертки следует возможность представить выражение (1. 28) в несколько ином виде:

 

.

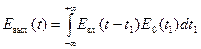(1. 30)

 

Уравнения, связывающие входной и выходной сигнал для нечувствительных к сдвигу систем, могут быть распространены на системы с двумя, а в общем случае и с большим количеством аргументов.

 

Интегральные выражения свертки предлагается в целях сокращения записи заменить символом " " [6]:

 

(1. 31)

 

что для рассматриваемых преобразований дает

 

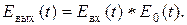
(1. 32)

 

Таким образом, зная сигнал на входе линейной и инвариантной к сдвигу системы, а также импульсную реакцию системы (отклик ее на единичный импульс), по формулам (1. 28) и (1. 30) можно математически определить сигнал на выходе системы, не реализуя физически саму систему.

К сожалению, из указанных выражений невозможно непосредственно найти одну из подынтегральных функций E_вх(t) или E₀(t) по второй и известному выходному сигналу.

Если линейная, нечувствительная к сдвигу система состоит из нескольких, последовательно пропускающих сигнал фильтрующих звеньев, то импульсная реакция системы представляет собой свертку импульсных реакций составляющих фильтров, что в сокращенном виде можно записать как

 

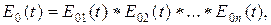
(1. 33)

 

где E₀₁(t), E₀₂(t), …, E_0n(t) – импульсные реакции составляющих систему фильтров;

E₀(t) – импульсная реакция системы в целом.

Для обеспечения удобства сравнения характеристик различных фильтров импульсную реакцию можно нормировать условием [11]

 

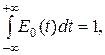
(1. 34)

 

что соответствует сохранению неизменного значения постоянной составляющей сигнала при фильтрации (это станет очевидным при анализе фильтрации в частотной области).

Пример. Рассмотрим преобразование оптического сигнала при получении на светочувствительном материале миры с косинусоидальным распределением интенсивности. Мирой называется решетка или ее изображение, состоящие из группы полос определенной ширины. Распределение яркости в решетке обычно имеет прямоугольный или косинусоидальный характер. Миры необходимы для экспериментального изучения свойств фильтров оптических сигналов.

Схема устройства для записи косинусоидальной миры представлена на рис. 1. 8.

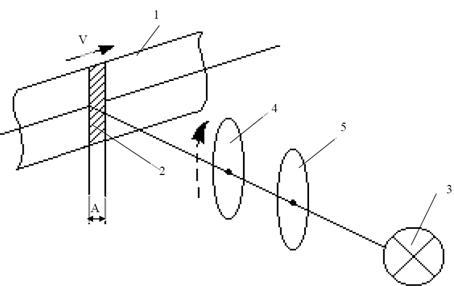
Рис. 1. 8. Схема устройства для получения миры
с косинусоидальным распределением интенсивности

Равномерно перемещающуюся со скоростью v фотопленку 1 освещают через щель 2 шириной A. Изменение освещенности во времени производится по косинусоидальному закону. Это достигается за счет прохождения светового пучка через осветительную систему 3 и два поляроидных фильтра 4 и 5. Поляроидный фильтр 4 равномерно вращается, фильтр 5 неподвижен. Вращение оси подвижного поляризатора относительно неподвижного обеспечивает косинусоидальное изменение интенсивности проходящего светового пучка. Уравнение изменения освещенности E(t) в плоскости щели имеет вид:

 

E(t) = a0 + acosw1t,

(1. 35)

 

где  a₀ – постоянная составляющая освещенности;

a – амплитуда переменной составляющей;

w₁ – угловая частота изменения освещенности;

t – время.

Так как светочувствительный материал равномерно перемещается со скоростью v вдоль оси x, независимую переменную t можно представить как отношение x/v и перейти к уравнению входного сигнала E(х) в функции пространственной координаты x:

 

(1. 36)

 

Фильтрами в рассматриваемой системе являются щель и фотопленка. Так как подробный анализ свойств светочувствительных материалов будет приведен ниже, то проанализируем только фильтрующее действие щели 2. Импульсную реакцию E₀(х) щели 2 шириной A можно представить в виде:

 

(1. 37)

 

Выходным сигналом Е_вых(x) является пространственное распределение освещенности в плоскости фотопленки:

 

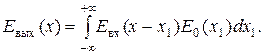
(1. 38)

 

Подстановка в это уравнение выражений для Е_вх и E₀ дает

 

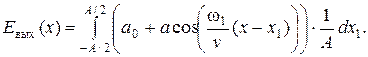
(1. 39)

 

Представление косинуса разности как суммы произведений косинуса и синуса и замена интеграла суммы суммой интегралов упрощает дальнейшее интегрирование:

 

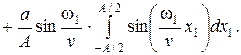
(1. 40)

 

Последний интеграл обращается в нуль, т. к. подынтегральная функция нечетная, а пределы интегрирования симметричны. Вычисление двух первых интегралов дает:

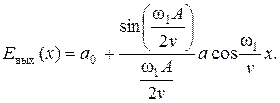
(1. 41)

 

Так как

 

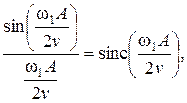
то окончательный вид уравнения сигнала на выходе щели следующий:

 

 

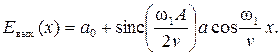
Сравнение Е_вых(x) и Е_вх(x) показывает, что они отличаются лишь наличием множителя в переменной части. График функции типа sinc представлен на рис. 1. 5. Она характеризуется осциллирующим с постоянным периодом убыванием от 1 до 0.

Следовательно, при увеличении значения аргумента этой функции, т. е. при росте произведения w₁A и уменьшении v, амплитуда переменной составляющей сигнала на выходе падает.

Кроме того, эта амплитуда будет обращаться в нуль, когда

 

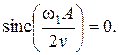
Это имеет место при

 

, где n = ±1, ±2…

 

В таком случае вместо миры на пленке получится равномерное почернение.

Изменения постоянной составляющей сигнала а₀ не произошло, т. к. импульсная реакция щели здесь являлась нормированной в соответствии с условием (1. 37).

Таким образом, регулируя параметры записи миры v, A, w₁, можно подобрать оптимальную для данного светочувствительного материала амплитуду переменной составляющей освещенности, равную произведению asinc ((w₁A)/(2v)), и предотвратить брак.

 

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: