 |
Зрительный анализатор человека
|
|
|
|
Зрительный анализатор человека
Аналоговым оптическим фильтром пространственных и временных частот является зрительный анализатор человека. Его АЧХ в области пространственных и временных частот были определены экспериментально для условия восприятия киноизображения [6]. При этом амплитуда гармонических сигналов на входе зрительного анализатора устанавливалась таким образом, чтобы выходной уровень сигнала соответствовал шуму глаза. Эксперименты показали, что в частотных областях ниже 10-12 Гц и 10-20 мм–1 в плоскости сетчатки зрительный анализатор не линеен, а в диапазонах 12-50 Гц и 20-
120 мм–1 может рассматриваться как линейный фильтр.
1. 7. Преобразования детерминированного сигнала и его спектра при дискретизации
При дискретизации непрерывный сигнал превращается в совокупность отдельных отсчетов, отстоящих друг от друга на период дискретизации T, чаще всего постоянный. На первый взгляд, восстановление промежуточных (" потерянных" ) значений сигнала невозможно. Однако теорема отсчетов гласит, что любой сигнал E(t), содержащий частоты не более fmax, можно с любой степенью точности передать с помощью отсчетов, следующих через период, равный 1/2fmax, если на выходе системы передачи расположен идеальный фильтр.
Под идеальным здесь понимают фильтр, имеющий форму прямоугольника и срез АЧХ на частотах –fmax, fmax. График АЧХ идеального фильтра представлен на рис. 1. 11а, его импульсная реакция на рис. 1. 11б.
В соответствии с теоремой отсчетов, чтобы ограничить спектр входящего в дискретизатор сигнала частотой fmax, необходимо поставить идеальный фильтр еще и на входе дискретизатора. Тогда система, обеспечивающая полное восстановление сигнала после дискретизации, представляет собой совокупность " идеальный фильтр на входе – дискретизатор – идеальный фильтр на выходе".
|
|
|
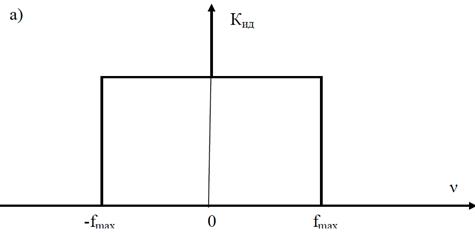
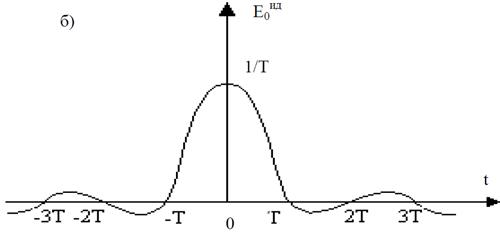
Рис. 1. 11. АЧХ (а) и импульсная реакция (б) идеального фильтра (Т = 1/(2fmax))
Схема такой системы представлена на рис. 1. 12. Входной идеальный фильтр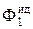 
обрезает частотные составляющие сигнала Eвх выше fmax, в результате чего сигнал E1 на выходе 
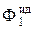имеет более " сглаженный" вид, чем Eвх (рис. 1. 13 а и б), а в спектре S1 " отрезаны" высокочастотные " хвосты" спектра Sвх. (рис. 1. 13 б и г).
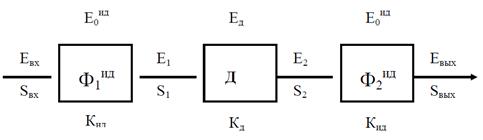
Рис. 1. 12. Схема системы, обеспечивающей полное восстановление
сигнала после дискретизации
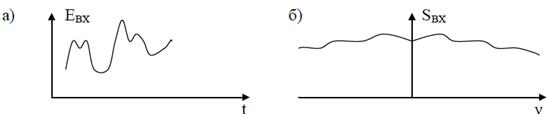
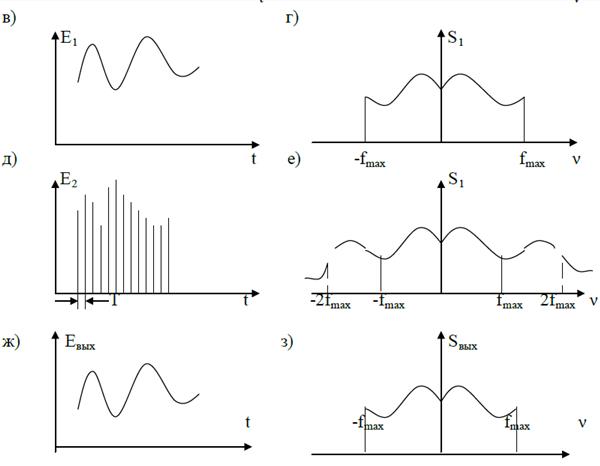
Рис. 1. 13. Схема преобразований сигнала и его спектра при использовании
на входе и выходе дискретизатора идеальных фильтров
Очевидно, что сигнал E1 есть свертка Eвх с импульсной реакцией идеального фильтра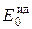 
, представляющей " синковую" функцию вида:
ш1
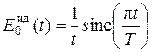
| (1. 48) |
где T – период дискретизации,
 .
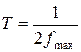| (1. 49) |
Спектр сигнала S1 – произведение Sвх и АЧХ идеального фильтра Kид:
| S1(v) = Sвх(v) · Kид(v). | (1. 50) |
Дискретизатор Д превращает непрерывный отфильтрованный сигнал E1(t) в ряд дискретных значений E2(t) (рис. 1. 13 д). Математически эта операция выглядит как произведение E1(t) на растровую функцию:
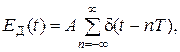
| (1. 51) |
где T – период дискретизации;
n – целое число;
d(t – nT) – дельта-функция Дирака;
A – постоянный коэффициент.
Так как
| (1. 52) |
где k – целое число, то из-за необходимости отсутствия размерности у растровой функции EД(t) в [15] принято: A = T. Поэтому выражение (1. 51) для растровой функции можно представить в виде
| (1. 53) |
По обратной теореме свертки произведению сигнала E1(t) и растровой функции EД(t) в спектральном пространстве соответствует свертка спектра S1(v) и спектра Kд(v) растровой функции, т. е. спектр S2(v) на выходе дискретизатора равен:
|
|
|
| S2(v) = S1(v) * Kд(v), | (1. 54) |
где
| (1. 55) |
Из (1. 48) следует, что спектр Kд(v) растровой функции также представляет из себя бесконечно длинную " расческу" из дельта-функций. Подстановка (1. 55) в (1. 54) дает:
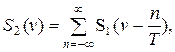
| (1. 56) |
т. е. спектр сигнала на выходе дискретизатора равен бесконечной сумме спектров сигнала на входе дискретизатора, смещенных относительно первоначального положения на значения, кратные обратному периоду дискретизации или частоте 2fmax (см. рис. 1. 13е).
Частота fд, равная 1/T или 2fmax, называется частотой дискретизации.
Восстановление дискретизированного сигнала осуществляется в идеальном фильтре на выходе системы (рис. 1. 14). Так как фильтр идеальный, то каждому входному дискретному импульсу (рис. 1. 14а) будет соответствовать " синковая" реакция на выходе (рис. 1. 14б-е), середина которой совпадает с положением импульса. Максимальное значение этой реакции пропорционально амплитуде импульса, ее нулевые значения приходятся на остальные точки отсчета (места расположения остальных импульсов). Сумма " синковых" откликов на каждый импульс и есть точно восстановленный сигнал до дискретизации (рис. 1. 14, ж). Таким образом, сигнал, в котором отфильтрованы до дискретизации составляющие, большие fmax, может быть полностью восстановлен при наличии навыходе дискретизатора идеального фильтра.
Но реализовать идеальный фильтр практически невозможно. Его импульсная реакция представляет собой " синковую" функцию (см. рис. 1. 14б), т. е. отклик на импульс в нулевой точке должен начинаться задолго (в минус-бесконечности) до самого импульса. Характеристики реальных фильтров, как аналоговых, так и цифровых, отличаются от идеальных, поэтому сигнал после дискретизации отличается от исходного в лучшем случае амплитудой частотных составляющих, в худшем – появлением искажений (ложных частотных составляющих).
Искажения, возникающие при дискретизации, делятся на две группы: первого и второго рода. Искажения первого рода возникают за счет неидеального фильтра до дискретизатора и проявляются как ложные низкочастотные составляющие в выходном сигнале. Искажения второго рода возникают за счет неидеальности фильтра на выходе дискретизатора и проявляются как ложные высокочастотные составляющие.
|
|
|
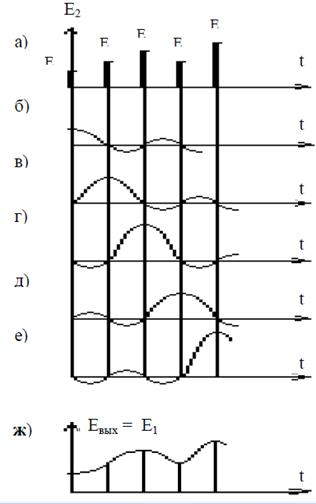
Рис. 1. 14. Сигнал после дискретизатора (а), отклик на каждый импульс (б – е),
восстановленный после искажений сигнал (ж)
Рассмотрим процесс возникновения искажений первого рода. Пусть фильтр до дискретизатора пропускает частоты большие fmax (рис. 1. 15а), на выходе дискретизатора – идеальный фильтр. Тогда спектр сигнала S1 перед дискретизатором может содержать составляющие, большие fmax. В результате дискретизации произойдет трансформация этих высокочастотных составляющих из смещенных АЧХ в низкочастотную область исходного спектра S1, причем они сохраняются после фильтрации идеальным фильтром на
выходе дискретизатора (рис. 1. 15б).
Если, например, сигнал оптический, а частоты пространственные, то на выходе системы дискретизации возникнут ложные структуры больших размеров (муар-эффект), которые не существуют в исходном изображении.
Исключить искажения первого рода возможно, выбрав период дискретизации T из условия:
 ,
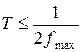| (1. 57) |
где fmax – максимальная частотная составляющая входного сигнала.
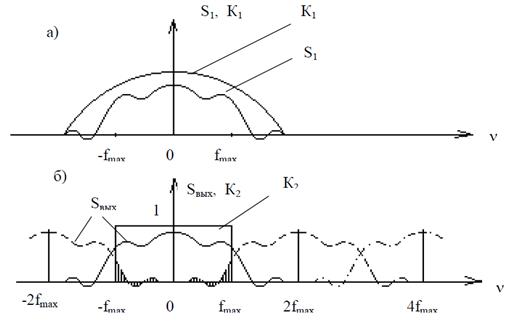
Рис. 1. 15. АЧХ сигнала S1, отфильтрованная неидеальным входным фильтром К1 (а) и АЧХ Sвых сигнала после дискретизации выходным фильтром К2 (б),
ложные составляющие заштрихованы
Использование реальных фильтров при соблюдении этого условия может привести к уменьшению амплитуды ряда частотных составляющих сигнала, но обеспечивает исключение искажений первого рода.
Проанализируем механизм возникновения искажений второго рода. Примем, что на входе дискретизатора – идеальный фильтр (рис. 1. 16а), на выходе – реальный (рис. 16б). Тогда выходной фильтр пропустит ложные высокочастотные составляющие из возникших при дискретизации смещенных АЧХ. Для оптического сигнала с пространственным аргументом искажения второго рода проявляются в виде ложных структур малого размера на исходном изображении. Избежать искажений можно, реализовав условие (1. 57), где fmax представляет собой границу частотной характеристики выходного фильтра. Если этот фильтр имеет не П-образную идеальную форму АЧХ, то при отсутствии частотных искажений произойдет уменьшение амплитуды некоторых составляющих.
|
|
|
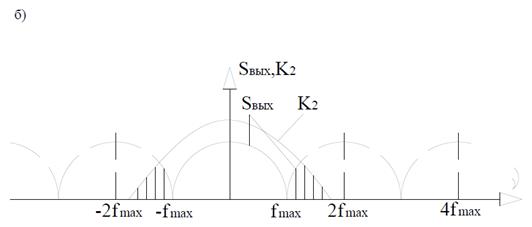
Рис. 1. 16. АЧХ сигнала S1, отфильтрованная идеальным фильтром K1 (a), и АЧХ сигнала Sвых после дискретизации и фильтрации выходным неидеальным фильтром K2 (б), ложные
составляющие заштрихованы
Очевидно, что появление частотных искажений (ложной информации) очень опасно и должно быть исключено правильным подбором характеристик фильтров и периода дискретизации.
|
|
|
