 |
1.5. Преобразование спектра детерминированного сигнала в линейных системах
|
|
|
|
В линейной, нечувствительной к сдвигу системе, удобнее осуществлять преобразование не самих сигналов, а их спектральных характеристик, т. к. в этом случае интегральная операция свертки заменяется операциями умножения и сложения.
Этот переход базируется на теореме свертки: преобразование Фурье свертки двух функций равно произведению преобразований Фурье исходных функций. Таким образом, равенствам (1. 32) и (1. 33) в спектральном пространстве соответствуют выражения:
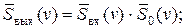
| (1. 42) | |
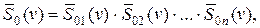
| (1. 43) |
где 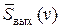 и
и 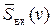 – спектральные плотности выходного и входного сигналов;
– спектральные плотности выходного и входного сигналов;
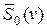 – комплексная частотная характеристика системы, представляющая Фурье-преобразование импульсной реакции;
– комплексная частотная характеристика системы, представляющая Фурье-преобразование импульсной реакции;
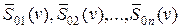 – комплексные частотные характеристики фильтров, образующих систему.
– комплексные частотные характеристики фильтров, образующих систему.
Подстановка выражения (1. 7) в формулы (1. 42) и (1. 43) позволяет осуществить переход от соотношений, связывающих спектральные плотности и комплексные частотные характеристики к уравнениям, содержащим амплитудно- и фазочастотные характеристики:
| Sвых(v) = Sвх(v) · S0(v); | (1. 44) | |
| qвых(v) = qвх(v) +q0(v); | (1. 45) | |
| S0(v) = S01(v) · S02(v) ·…· S0n(v); | (1. 46) | |
| q0(v) = q01(v) + q02(v) +…+ q0n(v), | (1. 47) |
где Sвых(v), Sвх(v) – АЧХ сигнала на выходе и входе системы;
qвых(v), qвх(v) – ФЧХ сигнала на выходе и входе системы;
S0(v), q0(v) – АЧХ и ФЧХ системы, вычисляемые по формулам (1. 5), (1. 6), (1. 8), (1. 9), куда вместо E(t) подставляется импульсная реакция системы E0(t);
S01(v), S02(v), …, S0n(v) – АЧХ фильтров, образующих систему;
q01(v), q02(v), …, q0n(v) – ФЧХ фильтров, образующих систему.
Из выражений (1. 44)–(1. 47) следует, что в пространстве спектров вместо интегральной операции свертки фильтрация характеризуется произведением АЧХ и суммой ФЧХ, причем, в отличие от свертки, где можно вычислить только выходной сигнал и импульсную реакцию системы в целом, в спектральном пространстве можно определить любой член выражений по известным остальным. Например, зная сигнал на выходе, а, следовательно, его АЧХ, ФЧХ, и соответствующие характеристики системы или фильтра, можно рассчитать АЧХ и ФЧХ входного сигнала, т. е. восстановить входной сигнал.
|
|
|
Такой простой способ восстановления исходной информации подразумевает отсутствие шума в сигнале и в канале его передачи. Непременное наличие шума в реальных системах, позволяет восстановить входной сигнал лишь с некоторой погрешностью.
Пример. Найдем АЧХ и ФЧХ сигнала в плоскости светочувствительного материала при получении миры с косинусоидальным распределением контраста (см. пример из раздела 1. 4). Сигнал Евх(x) представляет собой четную функцию, следовательно, его АЧХ Sвх(v) есть косинус-преобразование Фурье. Найдем Sвх(v), используя таблицы преобразований Фурье [7]:
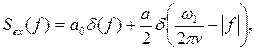
где f – пространственная частота, мм–1;
прочие обозначения приведены в предыдущем примере.
ФЧХ входного сигнала qвх(f) из-за его четности равна нулю.
Аналогично определяем АЧХ S0(f) и ФЧХ q0(f) щели, используя четность импульсной реакции:
S0(f) = sinc(pfA),
q0(f) = 0.
АЧХ Sвх(f) и ФЧХ qвых(f) на выходе щели найдем, используя формулы (1. 44) и (1. 45):

Выходной сигнал, или распределение освещенности в плоскости светочувствительного материала в силу четности АЧХ Sвх(f) можно найти, как ее косинус-преобразование:
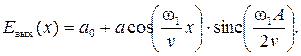
Очевидно, что определение выходных характеристик сигнала с использованием произведения в спектральной области удобней, чем с применением свертки (см. предыдущий пример).
|
|
|


